幾何学でみる重回帰の性質

投稿者: | 2019-08-13
0件のコメント

重回帰の各種性質の多くは行列、ベクトル計算で示すことできます。ただ、計算手順だけを追っても性質が成立する「仕組み」や「背景」を理解しづらいです。ここでは重回帰を幾何的に解釈しながら基本的な性質として

  • 射影による回帰係数の導出
  • 残差[math]\boldsymbol{\varepsilon}[/math]の性質
  • 出力データ[math]\boldsymbol{y}[/math]と予測値[math]\boldsymbol{\hat{y}}[/math]の平均値
  • 全変動の平方和の分解

を導きます。

重回帰モデル

重回帰は[math]P[/math]個の説明変数[math]x_{1},\ x_{2},\dots,\ x_{P}[/math]と目的変数[math]y[/math]の間の関係

[math]

y = \beta_0 + \beta_1 x_1 + \cdots + \beta_P x_P,\ \beta_0, \dots, \beta_P \in \mathbb{R}
[/math]

を[math]N[/math]個の学習データ、つまり入出力データの組

  • 入力データ: [math](x_{i,1},\ x_{i,2},\dots,\ x_{i,P}) \in \mathbb{R}^P[/math]
  • 出力データ: [math]y_i\in \mathbb{R}[/math]

から求める手法です[math](i=1,2,\dots,N)[/math]。

表記を簡単にするために行列、ベクトルを定義しておきます。

  • 説明変数: [math]\boldsymbol{x}=(1,x_1,\dots,x_P)^T\in \mathbb{R}^{P+1}[/math]
  • 回帰係数: [math]\boldsymbol{\beta}=(\beta_0,\beta_1,\dots,\beta_P)^T\in \mathbb{R}^{P+1}[/math]
  • 学習データ
    • 出力データ: [math]\boldsymbol{y}=(y_1,\dots,y_N)^T\in\mathbb{R}^N[/math]
    • 入力データ:
      [math]
      \begin{eqnarray}
      
\boldsymbol{e} &=& (1,\ 1,\dots,\ 1)^T\in\mathbb{R}^N \\
      \boldsymbol{x}_i &=& (x_{1,i},\ x_{2,i},\dots,\ x_{N,i})^T\in\mathbb{R}^N \\
      \boldsymbol{X} &=& \left(
\boldsymbol{e}\ 
\boldsymbol{x}_1 \cdots \boldsymbol{x}_P \right)\in \mathbb{R}^{N \times (P+1)}
      \end{eqnarray}
      [/math]

幾何学でみる重回帰モデル

回帰係数[math]\boldsymbol{\beta}[/math]に対し学習データでの予測値[math]\hat{y}_i=\beta_0 + \sum_p \beta_p x_{i,p}[/math]を並べたベクトルは

[math]

\begin{eqnarray}

\boldsymbol{\hat{y}} &=& \beta_0 
\boldsymbol{e} + \beta_1\boldsymbol{x}_1 + \cdots + \beta_P\boldsymbol{x}_P \\
&=& \boldsymbol{X}\boldsymbol{\beta}
\end{eqnarray}
[/math]

とかけます。入力データの線形結合で表現できる空間を

[math]

L(\boldsymbol{X}) = \left\{\beta_0 
\boldsymbol{e} + \beta_1\boldsymbol{x}_1 + \cdots + \beta_P\boldsymbol{x}_P \ |\ \boldsymbol{\beta}\in \mathbb{R}^{P+1}\right\}
[/math]

とし、学習データでの残差[math]\boldsymbol{\varepsilon}=

\boldsymbol{y}-\boldsymbol{\hat{y}}[/math]として図示すると下図になります。

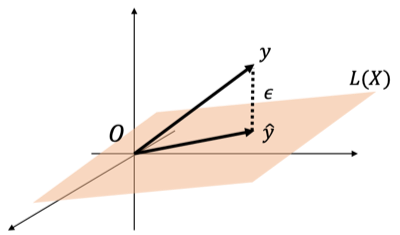
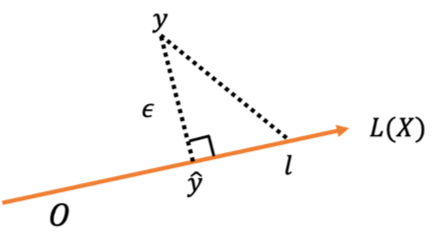
重回帰モデルは残差の二乗和[math]\|\boldsymbol{\varepsilon}\|^2[/math]を最小化する[math]\boldsymbol{\beta}[/math]を求める問題なので図において

空間[math]L(\boldsymbol{X})[/math]上で点[math]

\boldsymbol{y}[/math]との距離が最小になる点[math]\boldsymbol{\hat{y}}[/math]

を求める問題と等価になります。

射影による回帰係数の導出

空間[math]L(\boldsymbol{X})[/math]上のへ射影を考え、残差との直交性から回帰係数を求めることができます。

空間[math]L(\boldsymbol{X})[/math]上で点[math]

\boldsymbol{y}[/math]との距離が最小になる点[math]\boldsymbol{\hat{y}}[/math]は点[math]

\boldsymbol{y}[/math]を[math]L(\boldsymbol{X})[/math]に射影した点で与えられる。

[math]
\boldsymbol{\hat{y}} = \boldsymbol{X}\left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T\boldsymbol{y}
[/math]

まず空間[math]L(\boldsymbol{X})[/math]への射影行列を[math]\boldsymbol{H}[/math]とします。射影行列の性質から[math]\boldsymbol{H}^2=\boldsymbol{H},\ \boldsymbol{H}^T=\boldsymbol{H}[/math]であり次の性質が成立します。

任意の[math]\boldsymbol{l}\in L(\boldsymbol{X})[/math]と残差[math]\boldsymbol{\varepsilon}=\boldsymbol{y}-\boldsymbol{\hat{y}}[/math]は直交する。

まず[math]\boldsymbol{\hat{y}}=\boldsymbol{H}\boldsymbol{y}[/math]なので[math]\boldsymbol{\varepsilon}=\boldsymbol{y}-\boldsymbol{\hat{y}}=(\boldsymbol{I}-\boldsymbol{H})\boldsymbol{y}[/math]とかけます。また、[math]\boldsymbol{l}[/math]は適当な[math]\boldsymbol{l}’\in\mathbb{R}^N[/math]を用いて[math]\boldsymbol{l}=\boldsymbol{H}\boldsymbol{l}'[/math]とかけます。これより

[math]
\begin{eqnarray}

\boldsymbol{\varepsilon}^T \boldsymbol{l} &=& \boldsymbol{y}^T (\boldsymbol{I}-\boldsymbol{H})\boldsymbol{H}\boldsymbol{l}’ \\
&=& \boldsymbol{y}^T(\boldsymbol{H}-\boldsymbol{H}^2)\boldsymbol{l}’ \\
&=& 0
\end{eqnarray}
[/math]

より直交することがわかります。

次に点[math]\boldsymbol{y}[/math]を射影した点[math]\boldsymbol{\hat{y}}[/math]が空間[math]L(\boldsymbol{X})[/math]で[math]\boldsymbol{y}[/math]との距離が最小になることをみましょう。

[math]\boldsymbol{l}[/math]を空間[math]L(\boldsymbol{X})[/math]上の任意の点として

[math]
\begin{eqnarray}

\|\boldsymbol{y} – \boldsymbol{l}\|^2 &=& 
\|\boldsymbol{y} – \boldsymbol{\hat{y}} + \boldsymbol{\hat{y}} -\boldsymbol{l}\|^2 \\
&=& \|\boldsymbol{y} – \boldsymbol{\hat{y}}\|^2 + 2\boldsymbol{\varepsilon}^T(\boldsymbol{\hat{y}} -\boldsymbol{l})+\|\boldsymbol{\hat{y}}-\boldsymbol{l}\|^2
\end{eqnarray}
[/math]

であり[math]\boldsymbol{\hat{y}}, \boldsymbol{l}\in L(\boldsymbol{X})[/math]より[math]\boldsymbol{\varepsilon}^T(\boldsymbol{\hat{y}} -\boldsymbol{l})=0[/math]なので

[math]
\begin{eqnarray}


\|\boldsymbol{y} – \boldsymbol{l}\|^2 &=& \|\boldsymbol{y} – \boldsymbol{\hat{y}}\|^2 + \|\boldsymbol{\hat{y}}-\boldsymbol{l}\|^2 \\
&\geq & \|\boldsymbol{y} – \boldsymbol{\hat{y}}\|^2
\end{eqnarray}
[/math]

が成立し点[math]\boldsymbol{\hat{y}}[/math]で点[math]\boldsymbol{y}[/math]との距離が最小になることがわかります。

最後に射影行列を具体的に求めます。空間[math]L(\boldsymbol{X})[/math]と残差[math]\boldsymbol{\varepsilon}=\boldsymbol{y}-\boldsymbol{\hat{y}}[/math]が直交することから

[math]
\begin{eqnarray}
&&
\boldsymbol{X}^T\boldsymbol{\varepsilon} = 
0 \\
&\Leftrightarrow& \boldsymbol{X}^T(

\boldsymbol{y}-
\boldsymbol{X}
\boldsymbol{\beta}) = 0 \\
&\Leftrightarrow& \boldsymbol{X}^T
\boldsymbol{X}
\boldsymbol{\beta} = \boldsymbol{X}^T


\boldsymbol{y}
\end{eqnarray}
[/math]

と正規方程式が得られます。これより[math]N \geq P+1, {\rm rank}\ \boldsymbol{X}=P+1[/math]のとき

[math]
\boldsymbol{\hat{\beta}} = \left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T\boldsymbol{y}
[/math]

と回帰係数を求めることができます。これより

[math]
\begin{eqnarray}

\boldsymbol{\hat{y}} &=& 
\boldsymbol{X}
\boldsymbol{\hat{\beta}} \\
&=& \boldsymbol{X}
\left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T\boldsymbol{y}
\end{eqnarray}
[/math]

が得られ射影行列は[math]\boldsymbol{H} = \boldsymbol{X}
\left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T[/math]になります。

残差[math]\boldsymbol{\varepsilon}[/math]の性質

重回帰モデルの残差[math]\boldsymbol{\varepsilon}=\boldsymbol{y}-\boldsymbol{\hat{y}}[/math]は空間[math]L(\boldsymbol{X})[/math]と直交することから以下の性質が導けます。

残差[math]\boldsymbol{\varepsilon}=\boldsymbol{y}-\boldsymbol{\hat{y}}[/math]に対して以下が成立する。

  1. [math]\frac{1}{N}\sum_{i=1}^N \epsilon_i = 0[/math]: 残差の平均は0
  2. [math]Cor(\boldsymbol{\varepsilon}, \boldsymbol{x}_p)=0[/math]: 残差と各入力データは無相関

1つ目は[math]\boldsymbol{e}\in L(\boldsymbol{X})[/math]より[math]\boldsymbol{\varepsilon}^T\boldsymbol{e}=0[/math]から得られます。

2つ目は[math]Cor(\boldsymbol{\varepsilon}, \boldsymbol{x}_p)[/math]の分子は[math]\bar{x}_p[/math]を[math]\boldsymbol{x}_p[/math]の平均として[math]
\boldsymbol{\varepsilon}^T(\boldsymbol{x}_p – \bar{x}_p\boldsymbol{e})[/math]とかけ[math]\boldsymbol{x}_p, \boldsymbol{e}\in L(\boldsymbol{X})[/math]より

[math]

\boldsymbol{\varepsilon}^T(\boldsymbol{x}_p – \bar{x}_p\boldsymbol{e}) = 0
[/math]

なので[math]Cor(\boldsymbol{\varepsilon}, \boldsymbol{x}_p)=0[/math]が得られます。

出力データ[math]\boldsymbol{y}[/math]と予測値[math]\boldsymbol{\hat{y}}[/math]の平均値

残差[math]\boldsymbol{\varepsilon}=\boldsymbol{y}-\boldsymbol{\hat{y}}[/math]の平均が0になることから以下がわかります。

出力データ[math]\boldsymbol{y}[/math]の平均[math]\bar{y}[/math]と入力データの予測値[math]\boldsymbol{\hat{y}}[/math]の平均[math]\bar{\hat{y}}[/math]は一致する。

簡単な計算から示すことができます。

[math]
\begin{eqnarray}
\bar{y} – \bar{\hat{y}} &=& 
\dfrac{1}{N}(\boldsymbol{y}-\boldsymbol{\hat{y}})^T\boldsymbol{e} \\
&=& 
\dfrac{1}{N}\boldsymbol{\varepsilon}^T\boldsymbol{e} \\
&=& 0
\end{eqnarray}
[/math]

全変動の平方和の分解

出力データ[math]\boldsymbol{y}[/math], 入力データの予測値[math]\boldsymbol{\hat{y}}[/math]に対して

  • 全変動の平方和: [math]S_T=\|\boldsymbol{y} – \bar{y}\boldsymbol{e}\|^2[/math]
  • 残差変動の平方和: [math]S_e=\|\boldsymbol{y} – \boldsymbol{\hat{y}}\|^2[/math]
  • 回帰変動の平方和: [math]S_R=\|\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}\|^2[/math]

と呼びます。重回帰での予測値に対しては以下が成立します。

全変動、残差変動および回帰変動の平方和について以下が成立する。

[math]

\|\boldsymbol{y} – \bar{y}\boldsymbol{e}\|^2 = \|\boldsymbol{y} – \boldsymbol{\hat{y}}\|^2 + \|\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}\|^2
[/math]

この式は

「全変動の平方和[math]S_T[/math]」を「残差変動の平方和[math]S_e[/math]」と「回帰変動の平方和[math]S_{R}[/math]」に分解

できることを示しています。

証明は残差[math]\boldsymbol{y}-\boldsymbol{\hat{y}}[/math]が[math]\boldsymbol{e}, \boldsymbol{\hat{y}}\in L(\boldsymbol{X})[/math]と直交することと[math]\bar{y}=\bar{\hat{y}}[/math]より

[math]
\begin{eqnarray}


&& \|\boldsymbol{y} – \bar{y}\boldsymbol{e}\|^2 \\
&=& 

\|\boldsymbol{y} – \boldsymbol{\hat{y}} + \boldsymbol{\hat{y}} – \bar{y}\boldsymbol{e}\|^2 \\
&=& \|\boldsymbol{y} – \boldsymbol{\hat{y}}\|^2 + 2(\boldsymbol{y} – \boldsymbol{\hat{y}})^T(\boldsymbol{\hat{y}} – \bar{y}\boldsymbol{e}) + \|\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}\|^2 \\
&=& \|\boldsymbol{y} – \boldsymbol{\hat{y}}\|^2 + \|\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}\|^2
\end{eqnarray}
[/math]

が成立します。

シリーズ記事

「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「重回帰」の性質を紹介しています。

誤差項について「無相関で分散一定」「独立同一な正規分布」を仮定するとで様々な性質を導くことができますが、ここでは誤差項について特に仮定せずに導ける性質として

  • 考え方と基本的な性質: 回帰係数の導出、回帰超平面の性質、計算量との関係
  • 幾何学的な解釈（本記事）: 重回帰の性質を幾何的に導出
  • 決定係数: 決定係数と相関係数の関係
  • 多重共線性

を解説しています。

また行列やベクトル演算が多く何をしているか理解しづらいと感じた方は説明変数が1つの場合である「単回帰」も参照ください。

スポンサーリンク

関連記事

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です