仮説検定の過誤と検出力関数

仮説検定で帰無仮説の棄却／採択をする際、次の2種類の誤りをする可能性があります。

[math]\theta\in \Theta_0[/math]つまり帰無仮説が真であったが、誤って帰無仮説を棄却してしまう
[math]\theta\notin \Theta_0[/math]つまり対立仮説が真であったが、誤って帰無仮説を採択してしまう

それぞれ「第一種過誤(Type I Error)」「第二種過誤(Type II Error)」と呼びます。

		検定結果
		[math]H_0[/math]を採択	[math]H_0[/math]を棄却
真実	[math]H_0[/math]	○	第一種過誤
真実	[math]H_1[/math]	第二種過誤	○

一種、二種と数字が振られているだけの中身と関連が低い残念なネーミングで、未だに

あれ？第一種過誤ってどっちだっけ？？

となります。覚えにくいことで悪名高い^[1]教科書”Statistical Inference”でも”These two types of errors traditionally have been given the non-mnemonic names, Type I error and Type II … Continue readingこともありいくつか覚え方が知られています。有名なものは第一種過誤、第二種過誤をそれぞれ[math]\alpha[/math]エラー、[math]\beta[/math]エラーとも呼ぶことから（数字順とアルファベット順が同じなので覚えやすいでしょう）

第一種過誤[math]=\alpha[/math]エラー: 本当は帰無仮説が正しかった（有意差がなかった）のに帰無仮説を棄却（有意差がある）としてしまう「あ」わてんぼうさん
第二種過誤[math]=\beta[/math]エラー: 本当は対立仮説が正しかった（有意差があった）のに帰無仮説を棄却しない（有意差がない）としてしまう「ぼ」んやりさん

なので[math]\alpha[/math]と「あ」、[math]\beta[/math]と「ぼ」を対応づけて

「あ」わてんぼうの[math]\alpha[/math](第一種過誤)
「ぼ」んやりの[math]\beta[/math](第二種過誤)

と覚えます。

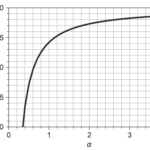
これら2つの過誤が小さい検定方法が「良い検定」と言え、その評価尺度として用いられる検出力関数(power function)を紹介します。

検出力関数

ある仮説検定の棄却域を[math]R[/math]とすると

第一種過誤: [math]P_\theta(X\in R), \theta\in\Theta_0[/math]
第二種過誤: [math]P_\theta(X\in R^c)\left(=1-P_\theta(X\in R)\right)[/math], [math]\theta\in\Theta_0^c[/math]

と書くことができます。いずれも[math]P_\theta(X\in R)[/math]を使って表現でき、この[math]P_\theta(X\in R)[/math]を検出力関数と呼び仮説検定の評価尺度として用います。

棄却域を[math]R[/math]とする仮説検定に対して

[math]
\beta(\theta) = P_\theta(X\in R)
[/math]

で定義される[math]\beta(\theta)[/math]を検出力関数と呼ぶ。

検出力関数から見ると

[math]H_0[/math]が真の場合[math](\theta\in\Theta_0)[/math]: 第一種過誤が生じる確率
[math]H_1[/math]が真の場合[math](\theta\in\Theta_0^c)[/math]: [math]1-[/math]第二種過誤が生じる確率

なので

[math]
\beta(\theta)\approx
\begin{cases}
0 &(\theta\in\Theta_0) \\
1 &(\theta\in\Theta_0^c)
\end{cases}
[/math]

となる検出力関数が望ましいと言えます。ところが第一種過誤、第二種過誤は通常トレードオフの関係にあるので、第一種過誤を固定した上で第二種過誤をどこまで小さくできるかを検討します。そこで第一種過誤を固定した仮説検定を定義します。

[math]0\leq \alpha \leq 1[/math]に対し[math]\sup_{\theta\in\Theta_0} \beta(\theta)=\alpha[/math]である検定をサイズ[math]\alpha[/math]、もしくは有意水準[math]\alpha[/math]の検定と呼ぶ。

[math]H_0[/math]が真の場合([math]\theta\in\Theta_0[/math])にもっとも第一種過誤の発生確率が高くなるワーストケースを考え、その発生確率を[math]\alpha[/math]に固定した検定方法を考えていることになります。この[math]\alpha[/math]は慣習的には[math]1\%[/math]や[math]5\%[/math]が用いられることが多いです。

シリーズ記事

統計学
- 仮説検定
- 尤度比検定
- 仮説検定の過誤と検出力関数（本記事）
- 一様最強検出力検定とネイマン・ピアソンの補題
- 単調尤度比とKarlin-Rubinの定理

参考文献

Casella, G and Berger, R.L.(1990), Statistical Inference(Second Edition): Section 8.3.1 Error Probabilities and the Power Function

脚注[+]

脚注
↑1	教科書”Statistical Inference”でも”These two types of errors traditionally have been given the non-mnemonic names, Type I error and Type II Error.”（「この2つの過誤は慣習的に「第一種過誤」「第二種過誤」という覚えづらい名前で呼ばれている」）と書かれています。