【統計検定1級過去問】2016年（統計数理）大問3

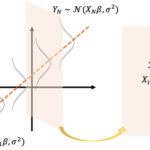
線形モデル[math]Y_i=\beta x_i+\epsilon_i\ (i=1,\dots,n)[/math]を考える。ここで

• [math]Y_i[/math]: 確率変数
• [math]x_i[/math]: 正の定数
• [math]\beta[/math]: 未知パラメータ
• [math]\epsilon_i[/math]: 互いに独立な確率変数で[math]E[\epsilon_i]=0,\ V[\epsilon_i]=\sigma^2[/math]

とする時、以下の問に答えよ。

1. [math]b_0=\dfrac{1}{n}\displaystyle\sum_{i=1}^n{\dfrac{Y_i}{x_i}},\ b_1=\dfrac{\sum_{i=1}^{n}Y_i}{\sum_{i=1}^{n}x_i}[/math]はそれぞれ[math]\beta[/math]の不偏推定量であることを示せ。
2. [math]\beta[/math]の最小二乗推定値[math]\beta_2[/math]および[math]E[\beta_2][/math]を求めよ。
3. [math]V[\beta_0],\ V[\beta_1],\ V[\beta_2][/math]を求めその大小を比較せよ。