今週のまとめ
- イルミネーションを見ながらLISの復元を考える
- Optuna論文を読んで発表した
- Grundy数を学んだ
- ABC285に出た。ちょっと冷えた
です。
(本文中にABC 043 D, 222 E, 284 D, 285 A-Eの解法を含む話題が出てくるのでご注意ください。)
1/8(Sun)
ライブラリ整備の続き。LIS(Longest Increasing Subsequence)をLibrary Checkerで試すとボコボコ落ちて、LISの復元が間違ってました。
LISを[math]O(N \log N)[/math]で出すために
DP_i[L] := 要素iまで見て長さLのLISの最後の要素の最小値
とするのが典型実装ですが、随時DP_iを書き換えていくので復元時にどの値を参照していいのかがややこしい。
例えば[math]A_i[/math]が「10, 9, 4, 5, 6, 1, 2」だと[math]A_7=2[/math]まで見て
[math]{\rm DP_7[1]=1, DP_7[2]=2、DP_7[3]=6}[/math]
でLISは長さ3になるんですが、このDPテーブルをどう見てもLIS=(4, 5, 6)を復元できない…というわけです。
うーん、どうしたものかなと考えながら夕方から次女のリクエストでハーベストの丘のライトアップへ。姉妹でも好みが全然違って次女はキラキラ系のインスタ映えしそうな場所が大好きです。

思っていた以上に本格的で良かったのですが困ったのが帰り。タクシーを呼ぼうとするもDiDiは捕まらずタクシー会社に電話をしても満車…。20分くらいかけて何とか配車してもらえましたがちょっとヒヤッとしました。カーシェアとか考えるかなぁ。
行き帰りでLISの復元を考えて
- DP_i[L]で最小値だけでなく、最小値の添え字も持つ
- DP_i[L]を更新した瞬間に添え字iとDP_i[L-1]の添え字を覚えておく
で復元できそうと分かって帰宅後に実装。無事、Library Checkerもパス。
1/9(Mon)
昼から奥さん、子どもたちはお出かけだったので家でのんびり。
先週のABC284 Dは途中で平方数の平方根を求める必要があって本番は二分探索した(週記の1/7参照)のですが、sqrt関数でいけたという話がTwitterで話題に。
round(sqrt(n))で大丈夫というのはまだわかる[1] … Continue readingのですが、(ll)sqrt(n)で大丈夫というはホント!?という感じ[2]浮動小数点は誤差が乗るのでsqrt(25)=4.99999となりえてキャストすると切り捨てられて意図しない結果になる。。どうやら平方数の平方根を正確に計算できるのは正しいようです。この日見たのはこちらの記事で後日、「浮動小数点数オタクがAtCoder Beginner Contest 284のD問題をガチで解説してみる」で詳細な解説を見ました。すげー[3] … Continue reading。
1/10(Tue)
夜に先週の週記をアップしたら「渋谷駅前で働くデータサイエンティストのブログ」さんにリツイートしてもらえました。Tweetのインプレッションが通常100くらいなのが一気に数千まで行ってさすがの影響力です。
1/11(Wed)
金曜に会社の研究会発表があってOptuna論文(“Optuna: A Next-generation Hyperparameter Optimization Framework“)を発表予定です[4]「日本人の英語なら読みやすいだろう」や「Optunaなら中身が大体わかるから楽だろう」という理由で選んだわけではないです。決して。。
Optunaはヒューリスティックコン参加者にはお馴染みのハイパーパラメタチューニングFWです。同じ目的を持ったものにHyperoptなどもあり違いを分かっていなかったですが調べてみて
- 機械学習の普及、発展でモデルが複雑化した
- NNの設計や変数選択など以前は職人技が必要だったタスクがハイパーパラメタチューニングで代替できるようになった
という背景があって
- より柔軟にNNの設計自体もチューニングしたくなった
- 効率的なパラメタの探索や枝狩り手法をうまく組合せたくなった
- 最後はマシンパワーでゴリ押したい
というニーズが高まってOptunaが生まれたという理解です。(人間って強欲ですね…)
確かに良く出来ていてて真ん中のパラメタ探索部分だけでも十分優秀です。発表用に適当なデータセットで手動チューニングしたものと比べましたが5分くらいで同等の性能のパラメタを見つけてくれました。
1/12(Thr)
ABC222のバーチャル参加
「E – Red and Blue Tree」で見事に詰まった…!
木とノードの番号列が与えられて、辺を赤か青に塗る。番号列順に最短路で移動した時に赤の辺の通過回数と青の辺の通過回数の指定の値[math]K[/math]にする塗り方を求める問題。
まず番号列順に最短路で移動するのはBFSを使えば十分間に合うので、実際に移動させて辺[math]e_i[/math]を何回通ったか数えてそれを[math]c_i[/math]とする。
ここで辺の塗り方を考えると赤だけ決めればよくて[math]c_i[/math]から何個か選んで合計を[math]\frac{T+K}{2}, T=\sum c_i[/math]にすればOK。これは部分和問題なのでDPで解ける。典型要素が組合さった面白い問題だったなーと提出するとWA!
その後、1時間ほどあーでもない、こーでもない…と続けてそのまま終了。

原因は部分和問題を解くDPで初期条件を
dp[0][0] = 1; dp[0][cl[0]] += 1;
とすべきを
dp[0][0] = 1; dp[0][cl[0]] = 1;
としていました[5]和を誤って代入にしていた。[math]c_0=0[/math]の時にズレが出る。。
サンプルは通るがWAという状況で当てもなくバグ探しをして時間を浪費してしまいました。振り返りとして
- 怪しそうなところを優先順位づけして網羅的にみる
- 問題の制約、定義域を確認する
- 定義域の境界をテストする
がちゃんとできていなくて今回だと
- 最短路とその復元はverify済なので部分和問題、入出力、最短路の順に怪しい
- 問題自体の制約に加えて自分で定義した部分和問題についても確認する
- [math]c_0=0[/math]は境界なのでチェックする
とすべきでした。さらにDPに関しては
- 初期条件と更新式がずれていることに気づいて妥当性を考える
- メモ化再帰に切り替えてみる
という動きもすべきで、さらにさらに
- 部分和問題は有名問題なのでググるなりライブラリ化すべき
だったなぁと反省です。
1/13(Fri)
会社の研究会でOptuna論文を発表。発表後にslackで「Optuna本予約しました!」と言っていた人がいたので布教に貢献。
ちなみに「自分のチューニング結果と同等の結果をOptunaは5分で見つけてくれた」と言ったら「Optunaと同等のパラメタ見つけられるなんてスゴイですね!」と言われました。Optuna先生は弊社でも信頼されています。
帰宅後に解いたABC_043「D – アンバランス」は面白い問題。
文字列[math]s[/math]が与えられるので部分文字列の中である文字が過半数を占めるもの(ここでは「過半列」と呼ぶ)を見つける問題。
[math]N\leq 10^5[/math]なので愚直解は間に合わず区間操作で考えてもうまく行きそうな性質がない。過半列の長さが3~5くらいのものを並べてみていると
長さ3以上の過半列は必ず長さ3の過半列を含む
のでは?というのに気づく。これは実際に正しいことが言える。
![]()
長さ3以上の過半列で長さ3の過半列を含まないものがあると仮定します。過半数を占める文字をXとするとXの前後2文字にはXが入らないことになります。(入ると長さ3の過半列ができる。)
この時、Xが占める割合は高々[math]1/2[/math](XYYXに並べた時)で過半列であることに反し矛盾。
これで「任意の長さの過半列を探す」問題から「長さ3の過半列を探す」問題になりこれは十分間に合います。
解説を見ると過半列になる必要十分条件は「XX」か「XYX」が現れることで、確かにこちらだと処理がシンプルでコーナーケースにもハマりにくい。
1/14(Sat)
鉄則本でNimを勉強。ちゃんと勉強したことがなかったので山崩しゲーム(「A33 – Game 2」)を自力で考えてみる。
[math]N=1[/math]は先手必勝、[math]N=2[/math]は石数が同数なら後手必勝、それ以外は先手必勝。[math]N=3[/math]は後手必勝のケースが少ないので書き出していくと規則がおぼろげに見えるもののキレイな性質が良く分からない…。半日考えてギブアップ。
各山の石数のXORを取って0なら後手必勝、それ以外は先手必勝になる。へーー。
解説は「組み合わせゲーム理論の基礎とGrundy数での勝敗判定アルゴリズム」が詳しく
- 二人ゼロ和有限確定完全情報ゲーム[6]このゲームは先手必勝、後手必勝、引き分けのどちらかが確定するでどちらの手番でも候補手が変わらないものを不偏ゲームという
- 不偏ゲームに対してGrundy数を定義できGrundy数が0かどうかで先手/後手必勝を判定できる
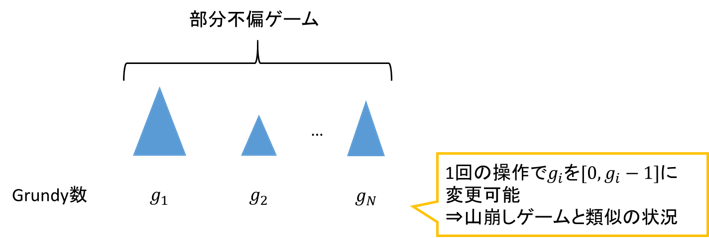
- 不偏ゲームを平行して行う場合は部分不偏ゲームのGrundy数のXORを使って先手/後手必勝を判定できる
になる。
スゴイのが3つ目で部分不偏ゲームの結果(山崩しだと一つの山の結果)をGrundy数で持っておくと全体の結果をXOR演算で出せる。
Grundy数を
「遷移先のGrundy数以外の最小の非負整数[7]Minimal EXcluded, MEXと呼ばれる。」
で定義するのがミソなのだろうが鉄則本でも記事でも証明は割愛されていたので結果だけを覚えておくので問題はなさそう。
この定理の正しさをざっくり考えると部分不偏ゲーム[math]i[/math]のGrundy数を[math]g_i[/math]とするとGrundy数の定義から1回操作でGrundy数を0以上[math]g_i[/math]未満のいずれにもできます。
これは山崩しゲームの状況と似ています。違いは後手がGrundy数を増やす[8]遷移先のGrundy数が[math]\{0, 1, 3\}[/math]の場合MEXは2ですが、3へ遷移することもできる。遷移をする可能性がありますが、この場合も
- ゲーム全体のXORが非ゼロの場合はゼロにできる遷移が存在
- ゲーム全体のXORがゼロの場合はどの遷移も非ゼロになる
が言え、不偏ゲームは有限回の操作で終了するのでXORがゼロかどうかでどちらが勝つかが分かる…というロジックになっていると思います。
この日は夜にここ2ヶ月サボっていた運動を再開。体力が落ちていたのでまずは5kmジョグ + 1kmウォーキングから。
1/15(Sun)
以前、1時間以上かかった or 解説ACした問題の復習。
みんなのプロコン2018「C – 駆引取引」は20分ほどで実装するもTLEが取れず2度目の敗退。原因は[math]O(2\cdot 2^N)[/math]だと思っていた箇所が実は[math]O(2^N\cdot 2^N)[/math]だったというお粗末な話。
ABC285の参加
「B – Longest Uncommon Prefix」は理解に時間がかかったというか、最初の理解は間違っててサンプル合わず。書かれていることをそのまま実装したら通りました。
「C – abc285_brutmhyhiizp」は26進数としてみればOK。
「D – Change Usernames」は[math]T_i[/math]と一致する[math]S_j[/math]がある場合、[math]j[/math]を[math]i[/math]より先に変更する必要があります。後はこれを満たした順番付けができるか?でこれはトポロジカルソートで判定できます。
「E – Work or Rest」は難しかった!1時間近くかけてAC。この問題の重要なポイントは
生産量は前後の休日との距離だけで決まる
です。ここから休日全体を平行移動しても全体の生産量は変わらないので最初の休日は曜日1に固定しても一般性を失いません。
円環に対するDPで良くある「先頭を固定して前から決めていき、最後に帳尻を合わせる」という考え方で解きます。
dp[i]: 1~i日目で最後の休日がi日目の場合の合計生産量の最大値
とします。休日間の間隔が[math]L[/math]日の場合のその間の平日の生産量を[math]p[L][/math]とすると
[math]dp[i] = \max_{L=1,..,i-1}(dp[i-L] + p[L])[/math]
となり[math]p[L][/math]を事前に求めておけば[math]O(N^2)[/math]で求まります。
あとは最後の帳尻合わせで最後の休日がi日目の時のi日目から[math]N[/math]日目の生産量を求めてその最大が解になります。
と、正解への流れだけ書くとすんなり解けたように見えますが、実際は
- i日目を平日/休日に決めようとして後ろに休日が来た場合の立式に苦悩する
- 実装で0-indexed, 1-indexedが混在してカオスになる
- [math]p[L][/math]の検算を「うん、なんか良さそう!」と適当な感覚でやった結果、デバッグに時間がかかる
- 境界をギリギリで書いてミスる
と色々とひどい感じでした。本番で通ると「あぁー間に合って良かった!」で終わりそうなのと、レートは落ちている[9]手ごたえ的にはギリ青パフォと思ったのですが…。レベル上がってません?のでちゃんと文字に起こして次回は少しでも良くしたいです。
関連記事
- 前週の週記: 「データサイエンティストという職業の1X年を振り返る」
- 翌週の週記: 「PCを注文するも…」
脚注
| ↑1 | といっても今回の問題だとnは[math]2^{62}[/math]くらいあってdoubleは仮数部が52bitなのでそもそも平方数を正しく表現できない可能性も十分あって自明な話ではないです。 |
|---|---|
| ↑2 | 浮動小数点は誤差が乗るのでsqrt(25)=4.99999となりえてキャストすると切り捨てられて意図しない結果になる。 |
| ↑3 | sqrtがIEEE754に準拠している場合、真の平方根に最も近い浮動小数点を返すことが保証されます。この時sqrtしてroundすると正しい値になることが計算機誤差を使った評価から分かります。さらにroundしなくても正しい値になることも示せるみたいですが、とても複雑なのでsqrtしてroundするのがベストプラクティスでしょう。 |
| ↑4 | 「日本人の英語なら読みやすいだろう」や「Optunaなら中身が大体わかるから楽だろう」という理由で選んだわけではないです。決して。 |
| ↑5 | 和を誤って代入にしていた。[math]c_0=0[/math]の時にズレが出る。 |
| ↑6 | このゲームは先手必勝、後手必勝、引き分けのどちらかが確定する |
| ↑7 | Minimal EXcluded, MEXと呼ばれる。 |
| ↑8 | 遷移先のGrundy数が[math]\{0, 1, 3\}[/math]の場合MEXは2ですが、3へ遷移することもできる。 |
| ↑9 | 手ごたえ的にはギリ青パフォと思ったのですが…。レベル上がってません? |






ピンバック: 週記(23/01/15週): | 有意に無意味な話
ピンバック: 週記(23/01/01週):データサイエンティストという職業の1X年を振り返る | 有意に無意味な話