ABC219「F – Cleaning Robot」

ABC219「F – Cleaning Robot」の解法メモです。

もともと週記で書いてましたが長くなったので分割しました。

問題概要

原点にいるロボットが格子点上を上下左右に移動する。移動の仕方は文字列[math]S, |S|\leq 2\times 10^5[/math]で与えられ、この操作を[math]K\leq 10^{12}[/math]回繰り返した時にロボットが通過する格子点の総数を求めよ。

考察

操作を繰り返すと格子点を重複して通過することがあるのでうまく重複を排除して数え上げることが必要です。

1回の操作後にいる座標を[math](X,Y)[/math]として[math](X,Y)=(0,0)[/math]の場合は1回分の操作で通る格子点の数を解答し、以下操作ごとにの終了位置は変わっていくものとします。

操作方向を左右反転、上下反転、X軸とY軸の取り換えても通る格子点の個数は変わらないので[math]X>0, Y\geq 0[/math]となるように前処理しておきます。

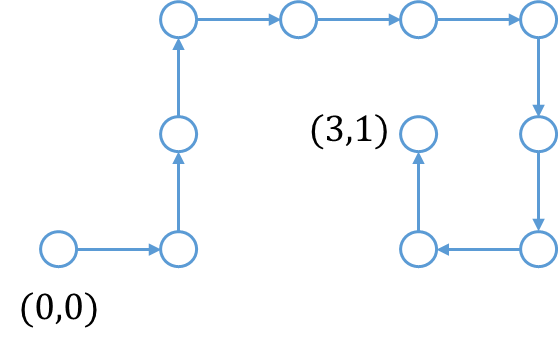
例えば上の図だと[math](X,Y)=(3,1)[/math]になります。この操作を繰り返すと

という動きになり

• 1回の操作ごとに(X, Y)だけ平行移動
• 各点はベクトル(X, Y)と平行な直線を移動

ということに注意します。特に２点目より各直線でどのようになるか？を考えればよく二次元の問題を一次元での考察に帰着できます。

ここで各点が操作を繰り返す時に何回、新規の点になるかを考えます。

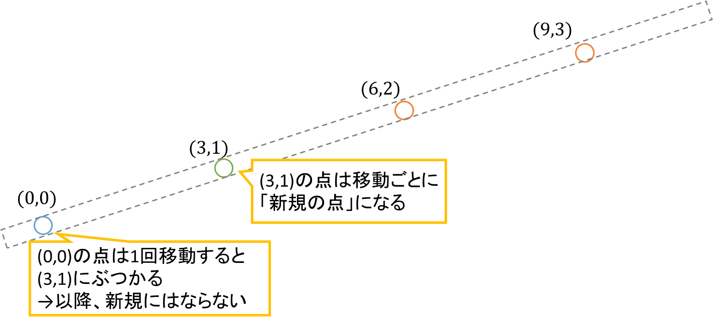
例えば点[math](0,0)[/math]は一度操作すると[math](3,1)[/math]に移り、すでにある点なのでこれ以降、新規の点と扱われることはありません。点[math](3,1)[/math]は[math]k[/math]回目の操作で[math](3+3k, 1+k)[/math]に移りますが他の点とぶつからず操作ごとに新規の点になります。

この観察から1回目の操作で通る点[math](x,y)[/math]を傾き[math]Y / X[/math]のどの直線に乗るかで分類し何回操作すると自分より前にある点にぶつかるかを求めその数を[math]C(x,y)[/math]とすると[math]\min(K, C(x,y))[/math]がその点が新規の点としてカウントされる回数になります。

これを初期配置のすべての点について求めた[math]\sum_{(x,y)}\min(K, C(x,y))[/math]が求める答えになります。これで良さそうですがまだワナがあって

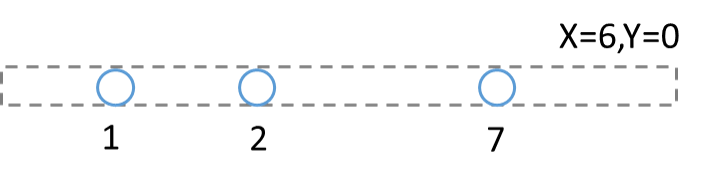
上記の状況だと1の点が最初にぶつかるのは2ではなくて7になり、2はどの点ともぶつからないです。（それぞれ[math]X=6[/math]ずつ進むので。）直線での分類に加えて[math]X[/math]で割った余りでも分類して最初にぶつかる点を求める必要があります。

実装

考察を元に以下の実装

1. 1回操作を行い最終点の位置[math](X, Y)[/math]を求める。原点に戻る場合は通過した格子点数を出して終了。
2. [math]X>0, Y\geq 0[/math]になるように左右反転、上下反転、X,Yの取り換えを行う
3. 1回目の操作で通過する点を「その点を傾き[math]Y / X[/math]の直線」「[math]X[/math]で割った余り」で分類し[math]X[/math]座標を記録
4. 同じ分類の中で何回の操作で自分より前（[math]X[/math]が大）の点にぶつかるかを求める
5. 各点の[math]\min(K, C(x,y))[/math]の合計を求める

で解が得られます。

計算量はステップ2が一番大きく[math]O(N\log N)[/math]になります。提出コードはこちらです。