RECRUIT 日本橋ハーフマラソン 2023冬(AHC018)参加記

2023年2月18～2月26日に開催された「RECRUIT 日本橋ハーフマラソン 2023冬(AHC018)」で過去最高の37位＆橙パフォ^[1]黄パフォもとったことがないのでかなり当たり回でした。でした！

ここ数回のAHCは考察、実装のどこかがズレててもどかしい結果が多かったですが、今回は観察、考察、実装＆実験の各パートがうまくつながって終了時に

やりたかったことはほとんど出来たな～

と思えるくらい自分としては納得のロジックを組むことができました。

他の方と比べると古参データサイエンティストらしく？地道にデータを取ってロジックを積み上げました。その内容を書き出したら結構なボリュームになりましたがお付き合いいただければ幸いです。

コンテスト／問題概要

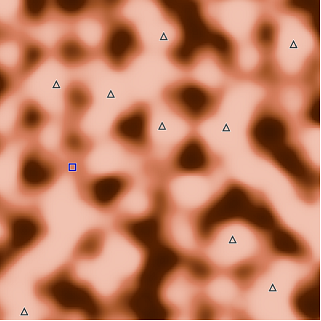
200 x 200のグリッド上に[math]K(1\leq K \leq 10)[/math]個の家と[math]W(1\leq W \leq 10)[/math]個の水源が与えられます。各セル[math](h,w)[/math]にはあるルールでランダム生成された頑丈さ[math]S_{h,w}[/math]が設定がされていますが入力では与えられません。

各セルを[math]P[/math]で掘削すると体力を[math]P+C[/math]だけ消費し、頑丈さを[math]P[/math]減らすことができます。頑丈さが0以下になるとそのセルを破壊でき水を流すことができます。家と水源を連結するのに必要な消費体力(ここではコストとします)を最小化する問題です。

観察＆初期考察

頑丈さは与えられないので推定する必要があります。今回は提供ツールで頑丈さを含めたテストケースを生成することができます。

テストケースを1万個生成していくつか眺めつつ基本的な統計量を取ってみます。

まず上の図(seed=0)のように所々に頑丈さの高いエリア（山）がある一方で低いエリア（平地）が続くことも多いです。実際に頑丈さの分布を取ると

(左が0～5000の図、右が10～30に絞った図)

• 100以下が37%
• 250以下で50%
• 1000以下でも74%

と値が小さい領域に寄っていますがだらだらと裾が長い分布だとわかります。「山」がそれなりにあるのでうまく回避したルートを作れるかが鍵になりそうです。

次に真の頑丈さが仮に分かったとして消費体力が最小になる経路を求めてみましょう。これは最小シュタイナー木問題^[2]参加中は最小シュタイナー木問題のことは知らず終了後にTwitterで知りました…でNP困難なので貪欲法で解(理論解とします)を作ってみます。seed=0だと

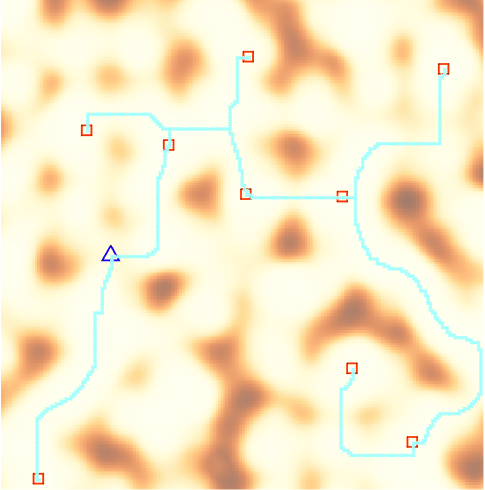
平地を通ってつなぐことができます。多くのサンプルで平地を通ってつなぐことができますがたまに陸の孤島とも呼べる場所に家/水源があるサンプルもあります。

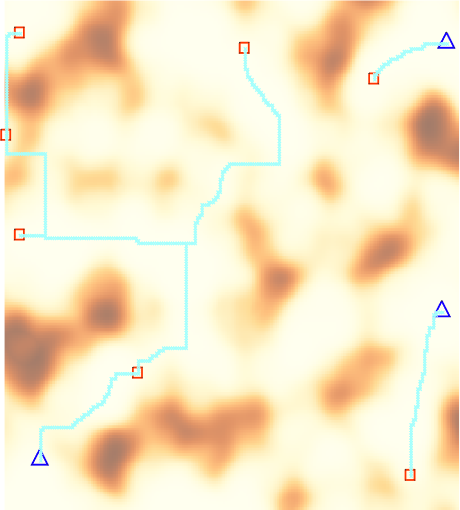
例えばseed=6だと左上の家は山を突っ切って水を届ける必要があります。

理論解での頑丈さの分布のパーセンタイル点を調べると

• 50%点: 18
• 70%点: 46
• 80%点: 84
• 90%点: 179
• 98%点: 493

とほぼ500以下で構成されていることが分かります。ここから

距離最小でつなぐのを目指しつつ山がありそうなら頑丈さ500以下の迂回路を探す

という基本方針でロジックを組むことにしました。

ロジック構成

全部をまとめて解くのは難しいので大きく3つに分けてロジックを作りました。

1. 周辺の頑丈さの推定
2. 周辺の頑丈さをもとに経路の探索
3. 体力ロスの少ない掘削パワーの設定＆ルート生成

周辺の頑丈さの推定

まず家はすべて掘削する必要があるので破壊できるまで掘削します。後続の「体力ロスの少ない掘削パワーの設定」でできるだけ真の頑丈さに近い値が欲しいので細かめに刻んで破壊します^[3]具体的には家/水源の頑丈さ分布の50%点, 75%点, 80%点以下5%点刻みになるように掘削。

頑丈さ分布の正確さとコストのトレードオフがあるので[math]C[/math]の値に応じてグリッド幅[math]D[/math]を決めて^[4][math]C[/math]に応じて8～10を設定。ただ、終了後のTweetをみるともう少し大きくてもよかったようです。グリッド上の点のみ掘削します。

ここでも統計の力を借りることができて掘削して破壊できなかった時に真の頑丈さをある程度推定できます。

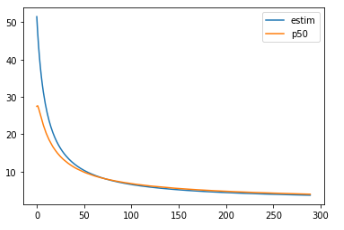
オレンジ線は「下限値[math]L[/math]が分かった時の真の値分布の50%点[math]S_{50}[/math]との比[math]S_{50}/L[/math]」の分布です。

[math]L\geq 50[/math]だと[math]S_{50}/L\approx 500/L+2[/math]で近似(青線)でき真の値は[math]S_{50}\approx 500+2L[/math]程度と推定できます。

ここから[math]P=50[/math]くらいで試し掘りして破壊できなければ理論解でほぼ通らないくらい頑丈なエリアと思ってよいことが分かります。

次にある頑丈さセルから距離[math]d[/math]だけ離れたセルの頑丈さは何倍位になるかを事前に集計しておきます。各グリッド点から距離[math]d[/math]離れたセルの頑丈さはグリッド点の推定した頑丈さに事前集計した倍率をかけて求めることができます。

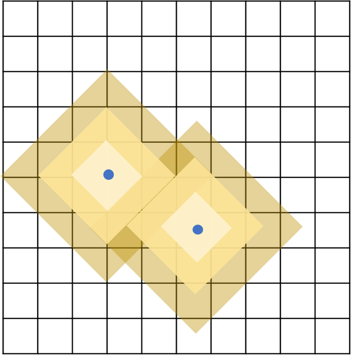
イメージ的には各グリッド点ごとにポテンシャルのような曲面があると思いそれを重ね合わせる^[5]重なった場所は推定した頑丈さの最小値を取りました感じです。

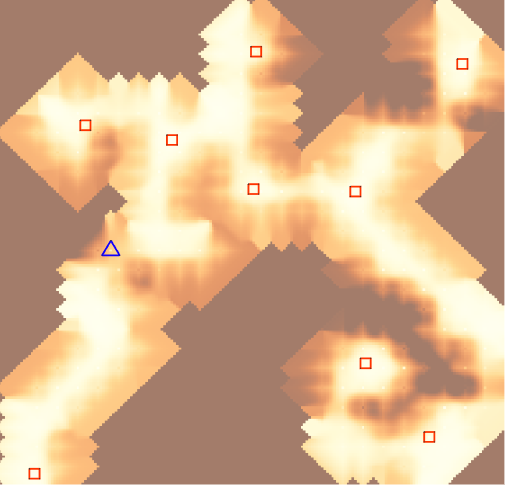
上の図は上記の考え方で推定したseed=0の頑丈さの分布です。結構、それっぽい頑丈さを推定できていると思います。

周辺の頑丈さをもとに経路の探索

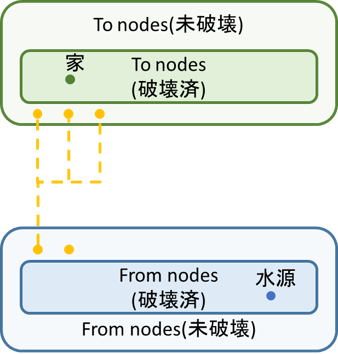
基本的には未接続の水源/家のうち最も近いものを近づけるように未破壊グリッドを掘削していきます。

ここでのポイントは頑丈さ未推定エリアの頑丈さを低めにしておくことです。

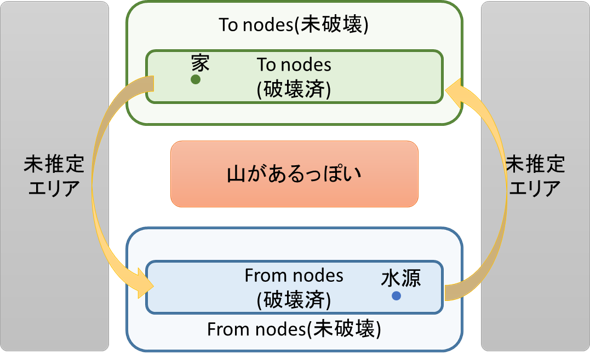
イメージとしてはまっすぐ進むと山にぶつかりそうなときに「理論解の大半で頑丈さが低いルートだったからまだ見てない領域にきっと低いルートがあるだろう」と楽観的に考えて周辺を探しに行くことに対応します。

もう一つポイントはFrom/Toの両方から掘削を進めることです。山に近づくと呼応するようにすそ野を探索してお互いに近づいていくのでVisualizerで見て結構感動しました。

あとseed=6のように陸の孤島が存在するサンプルもあるので一定コストをかけて連結にできなれば楽観探索をやめて山を突っ切るようにしました。

体力ロスの少ない掘削パワーの設定＆ルート生成

粗めのグリッドで連結できそうなパスが見つかったら最後にルートを生成します。

ここでも再び統計の力を借ります。ルート生成では隣接セルを掘削していくので頑丈さに高い相関があるだけでなく分布までほぼわかります。

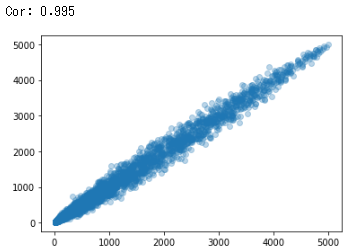
掘削するセルの頑丈さ分布が分かると何が嬉しいかというと

破壊に必要な体力(期待値)が最小になるパワーを期待値DPで出す

ことができます。

愚直に計算すると隣接セルの頑丈さごとに[math]O(P_{max}^2)[/math]かかるので事前に計算しておきます。さらに面白いことに「すでにかけたパワー」からみた「次にかける最適パワー」はほぼ線形になっており

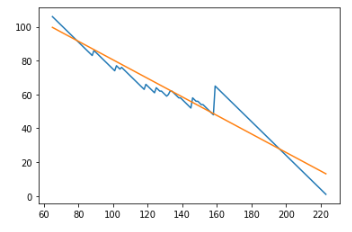
線形回帰して係数だけコードに埋め込みました。

ただ、隣接セルの頑丈さが正確に分かっていることが前提なので起点となる家/水源の頑丈さは多少回数を重ねてでも細かく刻んで正確に求めておくとルート生成全体が効率的に掘削できるようになります。

その他の工夫

[math]C[/math]の値によってコストの下げやすさが違うので

• パラメタチューニングは[math]C[/math]ごとに行う
• コストそのままの比較ではなく理論解のコストとの比で比較する

ようにしました。あと理論解との比較でコストの差分が

• 最初の周辺探索によるコスト増
• 理論解との経路の違いによるコスト増
• 掘削回数増によるコスト増

のどこで生じているのかを見て注力すべきポイントを判断するようにしました。

今回は「どこを改善したらいいのかの方向がつかめない」ということがあまりなく改善の方向を外さなかったのがよかったと思います。

逆に手が回らなかった改善ポイントは

• 水源をすべて掘削したが、頑丈さが高ければ放置する
• パラメタチューニングをグリッド幅と分布推定の広さ以外にも行う
• 家/水源はうまくつなぐと貪欲より良くなるので焼きなます

ですね。特に3つ目は最後、ギリギリで入れたのですがTLEになったので入れる前のものを最終提出としました。

最後に

今回は個別サンプルから気づいたことをデータで確認してうまくロジックに落とし込めたのと期待値DPで最適パワーを出すのに早い段階で気づけて周辺探索に力を割けたのがよかったと思います。

記事で触れたseed=0, 6の出力結果を載せるとseed=0が

でseed=6が

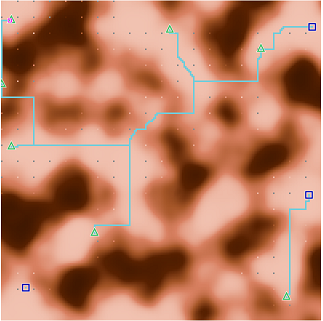
と納得できる探索ができています。自分が手でこの解を作れるか？と言われると正直無理なのでその意味で自分を超えたロジックを組むことができて大満足です。

と、この記事ではきれいな上澄み部分だけを書いたのですが実際には周辺探索はかなり苦労して最初ランダムに探索したら確率的なコーナーケースを踏んだりで散々でした。

ロジックがまとまったのが土曜の夜でそこから順位が大幅に上がったのですが、ラスト2時間は商品圏40位前後をふらふらしてダメ押しのつもりの解法がTLEで巻き戻すことになったりドキドキしっぱなしでした。この辺りは日記編で書こうと思います。

今回は考えたアイディアを実装し切ってそれがうまくいったので本当に楽しめました。主催者のリクルートさん、AtCoderの皆さん、参加者の皆さん楽しい1週間をありがとうございました！