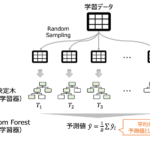
単変量モデル編では特徴量ごとにロジスティック回帰モデルを構築し精度評価を行いました。ここでは7つの特徴量を使って生存者を予測するモデルを構築します。
今までのモデルと比べ
- 互いに相関のある複数の特徴量を用いる
- モデルのハイパーパラメタのチューニングが必要
のため「モデルの正則化」や「交差検証(クロスバリデーション)」といった実践的な手法、考え方を紹介していきます。
前処理
ここでは扱いやすい以下の7つの特徴量を使います。
- チケットのクラス(Pclass)
- 性別(Sex)
- 年齢(Age)
- 一緒に乗船した兄弟、配偶者の数(SibSp)
- 一緒に乗船した親子の数(Parch)
- 運賃(Fare)
- 乗船港(Embarked)
また、欠損値補完として
- Fare: 欠損レコードの「Pclass=3」「Embarked=S」の平均運賃(=14.43)で補完
- Embarked: 欠損レコードは「Pclass=1st」。条件付き確率の最も高い「S」で補完
を行います。また、回帰系のモデルを使うため裾の長い分布のSibSp, Parch, Fareは外れ値処理を行います。この記事に対応するコードをGitHubにアップしているので合わせて見て、動かしていただくと理解が深まると思います。
年齢については単変量モデル編と同様にチケットクラスも考慮してカテゴリ化を行い、SibSp, Parchは0かどうかのフラグを追加します。
特徴量間の相関
ロジスティック回帰で複数の特徴量を用いる場合、特徴量間に高い相関があると数値的に不安定になりモデルが正しく求まらないといった問題が生じます。今回作った特徴量セットで相関を確認すると

といくつか相関の高いペアがあり、相関の高いペアを確認すると
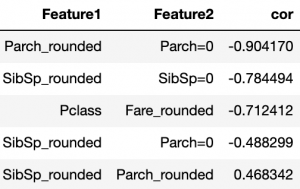
と派生させた特徴量間や「運賃とチケットクラス」、「SibSpとParch」間で相関が高いことがわかります。
「正則化」ロジスティック回帰
相関の高い特徴量がある場合の対処方法は
- ドメイン知識やAICなどの統計的基準を使って変数選択
- 主成分分析を使って直交化
などいくつか方法があるのですが、最近では「正則化」(regularization)アルゴリズムを使うことが多いです。
正則化アルゴリズムでは回帰係数を求める計算中に「モデルの複雑さに対するペナルティ」(=正則化項)も考慮することで
- 相関の高い特徴量があっても数値的に安定する
- 予測に寄与しない特徴量の回帰係数は小さくなり実質的な変数選択を行える
といった性質が知られています。最近では変数選択を行うより正則化アルゴリズムを使い正則化パラメタのチューニングで良いモデルを探ることが多くなってきています。
正則化ロジスティック回帰を使う際の注意点ですが各特徴量のばらつきが同じことを仮定しているため
各特徴量を標準化(分散を1に揃える)
する必要があります。
ハイパーパラメタのチューニング
今回は正則化ロジスティック回帰を使うため正則化を強さを表すパラメタ[math]C[/math]のチューニングが必要です。チューニングにあたり
- 交差検証(クロスバリデーション)
- モデル最適化指標にLogLossを利用
という2つの工夫を行います。
交差検証(クロスバリデーション)
「機械学習モデルのデータ分割/評価方法」で紹介したようにハイパーパラメタのチューニングが必要な場合、データセットを
- Train-Test-Validation分割
- 交差検証
で分ける必要があります。今回はデータ数がそこまで多くないので交差検証を使ってモデルの評価を行います。なお、データ分割時に乱数を使いますが、再現できるよう乱数シード値を固定するようにしましょう。
モデル評価指標
今までは精度(accuracy)でモデルを評価していましたがここからは次のLogLossと呼ばれる指標を使って評価します。
[math]
-\sum_i \left\{ y_i\log \hat{y}_i + (1-y_i)\log (1-\hat{y}_i) \right\}
[/math]
ここで[math]y_i, \hat{y}_i[/math]はサンプル[math]i[/math]の正解ラベル、モデルでの推定値になります。
最終的な評価指標がaccuracyなのでaccuracyで評価した方が良さそうですがLogLossは
- 通常、LogLossを小さくするとaccuracyも向上する
- 正解ラベル:1をギリギリ(ex. [math]51\%[/math]と予測)当てたのか余裕(ex. [math]99\%[/math]と予測)で当てたか、逆に間違いが大外しだったのか惜しかったのかも評価できる
- 微分ができるなど数学的に取り扱いやすい
といった良い性質があるので細かなチューニングを行う場合やXGBoostなど勾配ブースティング法を使いたい場合にはLogLossをモデル評価指標に用います。
モデル構築
チューニング
正則化ロジスティック回帰を
- 正則化パラメタ[math]C[/math]: [math]10^{-4},\dots,10^4[/math]をlogスケールで20等分
- 交差検証: 5分割
- モデル評価指標: LogLoss
でチューニングを行うと次の結果が得られます。
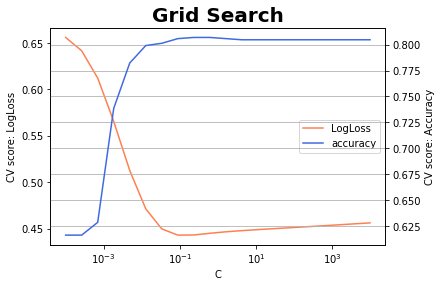
横軸が正則化パラメタ[math]C[/math]でオレンジ色の線がLogLossの値、青色の線が参考として精度(accuracy)を表示しています。
[math]C=0.089[/math]でLogLossが最小になりこの時の精度は0.806と[math]80\%[/math]を超えました。また、グラフからもLogLossの減少にあわせて精度も向上していることがわかります。
モデル確認
モデルの係数を確認[1]厳密にはz値をみるべきですが特徴量を標準化しているため係数をそのまま確認しています。すると

と「性別」「チケットクラス」「SibSp」「5才未満」などの項目が上位にきており探索的データ解析とも合致する結果になっています。
検証データで生存/死亡者の生存確率を推定しヒストグラムをとったのが下図です。
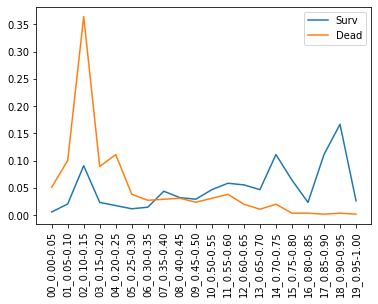
図から
- 生存者(青線)は確かに0.50より大きい領域に偏っている
- 死亡者(オレンジ線)は0.30未満に偏っている
- 0.15-0.20の領域には生存者が10%近く存在し改善の余地あり
とまずまずのモデルができていることがわかります。
評価結果
構築したモデルでテストデータを予測しSubmitすると精度は0.775でした。順位もおおよそ15,000人中6,000番くらいで上位半数に入ってきました。交差検証の精度0.806からは3%ほど悪化しましたが単変量モデルで一番よかった性別モデル(精度0.766)を上回ることができました。
評価結果をまとめると
- 交差検証でのLogLoss: 0.443
- 交差検証での精度: 0.806
- テストデータでの精度: 0.775
になります。
脚注
| ↑1 | 厳密にはz値をみるべきですが特徴量を標準化しているため係数をそのまま確認しています。 |
|---|