概要
データ解析コンペティション特集。データは(株)環のウェブ解析ツール「シビラ」サイトのWebアクセスログです。
前半二つの記事は「特徴シークエンス」抽出を用いてコンバージョンユーザ特有の行動を抽出しようと試みた内容。行動ログからあるグループに特徴的な行動を抽出するというのは仕事で出会ったテーマ(購買行動に至ったユーザの特徴抽出、作業が速いユーザの行動特性など)なので興味深い内容でした。ちなみにうちの会社は毎年新人がデータ解析コンペに応募するのが恒例となっていてて、3つ目の記事(「外部ソースを活用したウェブ・マーケティングのための分析フレームワークの提案」)は先輩たちによるものです。
ここでは前半2つの記事の概要を紹介します。
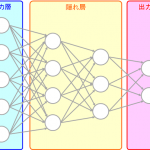
統合化顕在パターン判別モデルによるWebアクセスログデータの分析(羽室 行信,中西 正雄,山本 昭二)
概要
頻出パターン抽出を一般化し2群判別に適用したた顕在パターンを定義。コンペデータでコンバージョン群/非コンバージョン群を判別する顕在パターンを抽出し知見獲得を行います。
顕在パターン
通常の頻出パターンマイニングで扱う系列(トランザクションと呼ばれるアイテム集合の系列)に時間幅を入れ、時間が近いトランザクションは同一視する一般化系列パターンと呼ばれる概念を説明。パターンに対する
- 支持度: そのパターンの生起割合
- 成長率: あるグループAの支持度に対するグループBの支持度の比率
を定義します。支持度はそのパターンの発生頻度に対応し、成長率はそのパターンがある特定グループで偏って生じていると大きくなります。つまり、支持度/成長率が閾値以上であるようなパターンを抽出すればある特定グループで特徴的に生じるパターンであることが期待できます。
支持度/成長率が与えられた閾値以上のパターンを顕在パターンと呼びます。顕在パターンを利用した判別モデルの構築方法としてCAEP(Classification by Aggregating Emerging Patterns)を紹介。
パターン抽出の宿命ですが列挙しようとするとNP完全になることが多く計算量が爆発的に増えてしまします。そこで色々な剪定方法が提案されており記事中でも
- R-Interestingパターン(近接祖先の生起確率の期待値のR倍より小さなパターンを剪定。)
- 必須顕在パターン(包含関係にある顕在パターンのうち包含されているパターンの支持度、成長率が高ければ他方を剪定)
が紹介されています。いずれも「細かすぎるパターン」の抽出を回避するための手法と言えますね。
コンペデータへの適用
コンペデータでは
- URL
- リファラ
- 検索語
- 曜日
- 時刻帯
をアイテムとし、グループとして
- 直帰/滞在
- 申込/未申込
のそれぞれで顕在パターンを抽出しています。
「直帰/滞在判別モデル」では
- 検索語「シビラ」は平日、勤務時間内なら滞在確率が高くなる一方、休日だと直帰確率が高い。ビジネスユーザがメインであること、同名異義語として検索してくるユーザの存在が推察される
- adwordsでアクセスする人は滞在する人が多いが、キャンペーンページでは直帰率が高くうまく誘導できていない
などの知見が得られています。
「申込/未申込判別モデル」では
- 「価格情報」「申込フォーム」「申込の流れ」など申込に特有なページへの複数アクセスが申込につながる可能性が高い
- 「平日」「勤務時間内」のアイテムが多く含まれておりビジネスユーザの利用が多いと推察
- 多くのパターンで複数のアイテムが含まれており時間幅20秒としているが、内容をじっくり読まずにアクセスしていると推定
などの知見が得られています。
最後に他のモデル(決定木、Naive Bayes, k-Nearest Neighbors)との比較し本手法の優位性は時系列を扱える点にあるとのこと。
所感
時間幅の概念を入れて一般化しているのは面白いですね。頻出パターンでよくある悩みである
- 「当たり前のルール」ばかり出てくる(成長率をうまく設定すればよいのだが、そのチューニングに手間がかかる)
- 面白いルールを抽出するにはアイテムの定義にある程度業務知見が必要なことが多い
- 本質的に計算量が多く、大規模なデータ and/or 繰り返して実行するのに不向き
の1つ目について、時系列を入れることで「予兆」が見えてくれば面白いと思います。本記事のコンペデータでは「申込したユーザが申込に必要なページを見ていた」など当たり前なルールしか出てきておらず予兆発見とまでは言えなさそうですがアプローチとしては面白いと思います。ただ、実際にビジネスで使うには3つ目の計算量に関して「どこまでスケールするのか」の見極めと、簡単に使えるツール整備ができていないと厳しい気がします。
グラフ縮約による主要なWeb巡回経路を利用したパターン分析(中原 孝信,森田 裕之,米田 知弘)
概要
ページ遷移をグラフ表現し、コンバージョン群に特徴的な部分パターンを抽出。
グラフ縮約
ページ遷移をグラフ化すると極端に密な部分と疎な部分が存在し共立的に巡回パターンを発見するのが難しい。そこで、ある経路の出現回数が一定頻度以上になるまでノードを縮約する。
進化型計算を利用した巡回パターンの発見
巡回行動を「閲覧ページID、閲覧時間、訪問回数」でリスト化。関心のあるグループAとそれ以外のグループBにユーザを分割し、パターンの支持度の差が大きくなるパターンを抽出する。2目的最適化問題として定式化して抽出を行う(MOEAと呼んでいる)。
この問題を解くことで多様な解(パターン)が得られた。パターンを確認すると
- 申込ユーザは申込確認を行いやすい
- 申込ユーザは価格確認を行いやすい
といったパターンが見られた。関心の程度と費用対効果比較を行っていると推察。