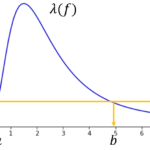
初中級者が解くべき過去問精選100問の中でも飛びぬけて難しい問題がこの「Surrounded Nodes」(ABC149 Fとして出題)です。
コメントでも
チャレンジ問題です。解けなくても、「そういう特殊な出力形式の問題ってあるんだな」と感じてほしいです。
とありますが初中級者には
- 数学的な考察が必要
- 実装も重い&ちゃんと設計しないとTLEになる
と難度が高いです。逆元がテーマですが、それがかすむほど難しい問題でした[1]最初に解いた時は半日かかって、2ヶ月後に解きなおした時も1時間くらいかかりました。
この記事では復習をかねて考察の流れを中心に説明します。
問題概要
[math]N[/math]頂点の木が与えられる。各頂点を確率1/2で独立に黒or白で塗る。黒い頂点を含む最小の部分木を[math]S[/math]とする。[math]S[/math]に含まれる白い頂点数の期待値を求めよ。
制限
- [math]2 \leq N \leq 2\times 10^5[/math]
- 実行時間制限は2秒
- 答えは有理数となるため[math]\mod 10^9+7[/math]で出力
考察
[math]N=2,3,4[/math]で実験
すぐに方針が思いつかなかったので小さなNで実験をしてみます。まず[math]N=2[/math]の場合、木としてあり得るのは1つしかなく塗られ方は[math]2^2=4[/math]通りあります。
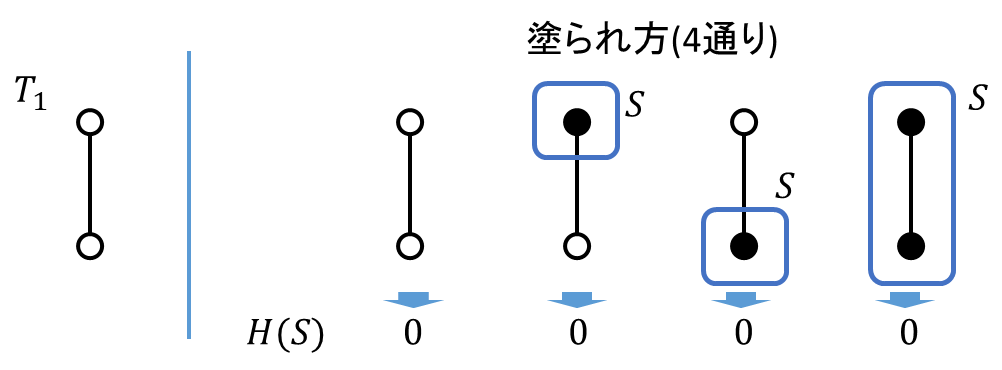
4通りそれぞれで黒い頂点を含む最小の部分木[math]S[/math]を求め、[math]S[/math]に含まれる白い頂点数[math]H(S)[/math]を数えるとこのケースではすべて0になります。
続いて[math]N=3[/math]も木としては1通りしかなく、塗られ方は[math]2^3=8[/math]通りあります。
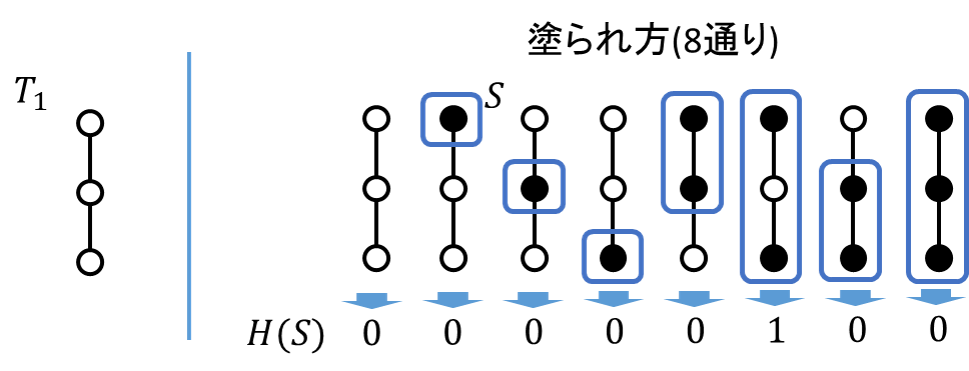
[math]S[/math]に白い頂点が含まれるケースがあり「黒-白-黒」の場合に[math]H(S)=1[/math]になります。
[math]N=4[/math]もみましょう。木としては2通りあります。まず一直線につながる形だと
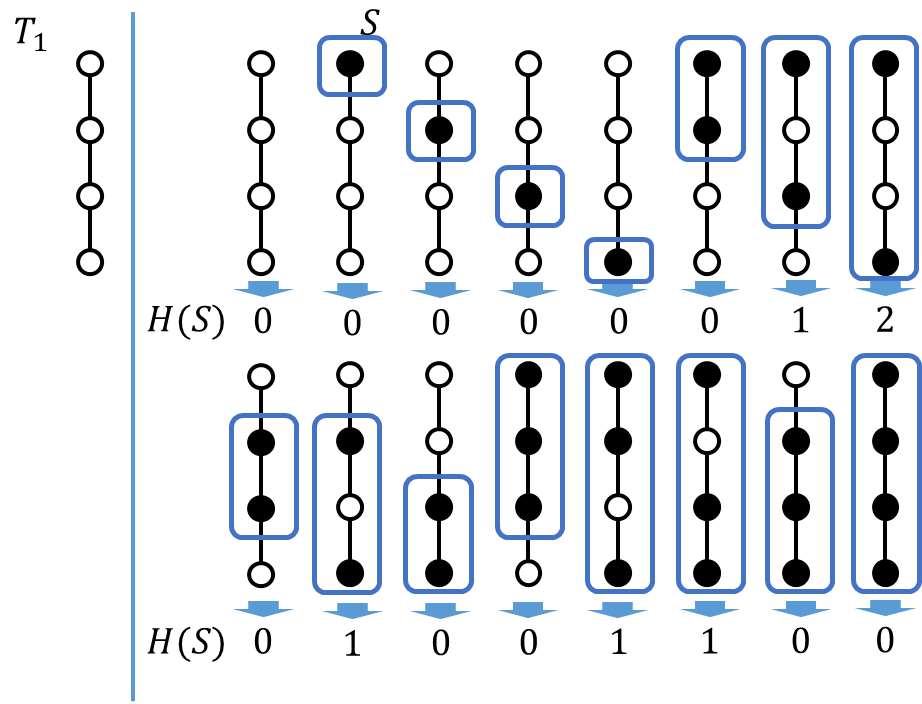
と白が黒に挟まれる形になると[math]H(S)>0[/math]となることが分かります。
[math]N=4[/math]の場合、もう一つ別の木の形がありこの場合は
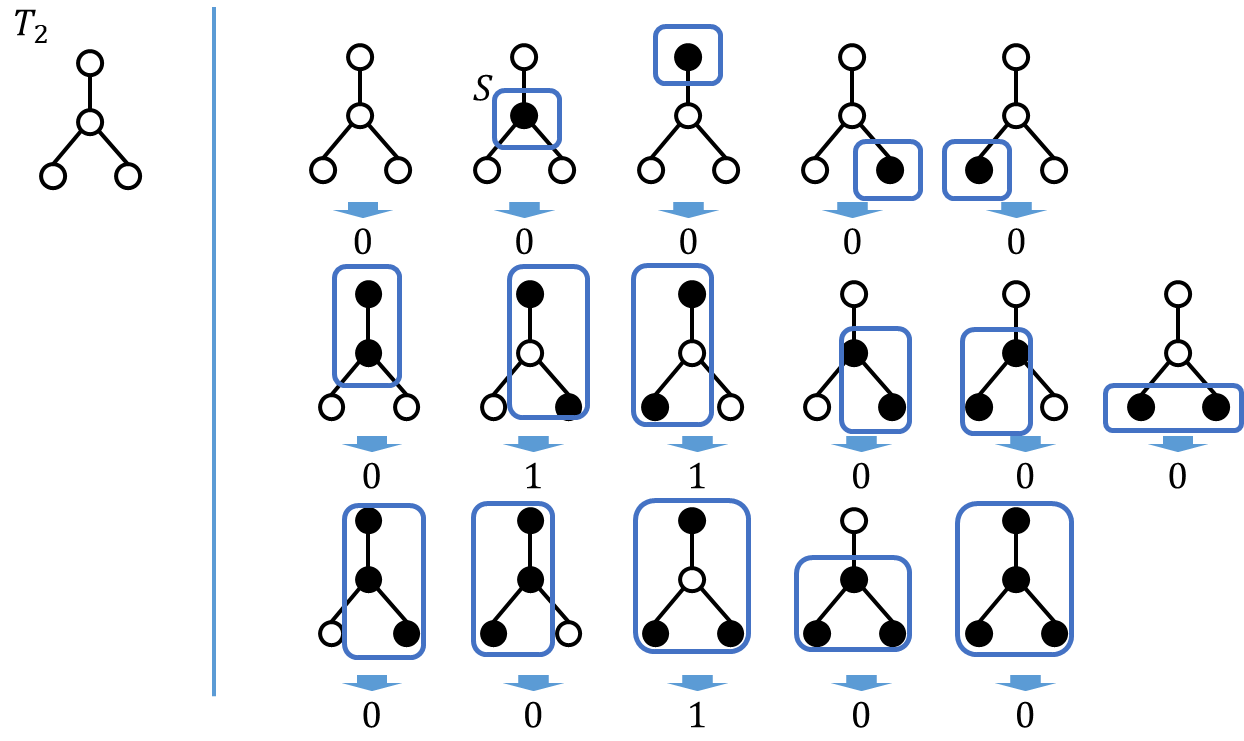
になります。これを観察すると
- 次数が1のノードは[math]S[/math]に含まれることはない
- 真ん中のノードが[math]S[/math]に含まれるのは隣接する3つのノードが2つ以上が黒の場合
が見えてきます。
[math]S[/math]に含まれるための必要十分条件
観察した内容を一般化すると
- 頂点[math]i[/math]の次数が2以上
- 頂点[math]i[/math]と隣接する部分木を[math]T_1,\dots,T_k[/math]とすると2つ以上の部分木[math]T_j[/math]が黒を含むこと
になる。
が言えます。
必要性は背理法で示します。

頂点[math]i[/math]が[math]S[/math]に含まれ隣接する部分木のうち黒を含むものが1個もしくは0個だとすると[math]S[/math]から頂点[math]i[/math]を除いても[math]S[/math]は黒い頂点をすべて含むことが言え[math]S[/math]の最小性に反します。
次に十分性は黒を含む部分木が2つ以上あると[math]S[/math]の連結性から頂点[math]i[/math]が含まれることが分かります。
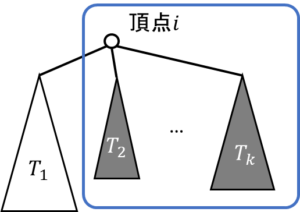
ここから頂点[math]i[/math]が[math]S[/math]に含まれる確率[math]P(i\in S)[/math]は頂点[math]i[/math]と隣接する部分木で黒を含む部分木が0個, 1個になる確率を[math]P_0(i), P_1(i)[/math]として
[math]
P(i\in S) = \dfrac{1}{2}\left(1-P_0(i)-P_1(i)\right)
[/math]
とかけます。(最初の1/2は頂点[math]i[/math]が白になる確率)
ここで部分木[math]T_j[/math]の頂点数を[math]n_j[/math]としこの部分木の頂点の少なくとも1つが黒になる確率は
[math]
P_B(n_j)=1 – (\frac{1}{2})^{n_j}
[/math]
となり、ここから
[math]
\begin{eqnarray}
P_0(i) &=& \prod_{j=1}^k \left(1 – P_B(n_j)\right) \\
P_1(i) &=& \sum_{l=1}^k P_B(n_l)\prod_{j=1, j\ne l}^k \left(1 – P_B(n_j)\right)
\end{eqnarray}
[/math]
と求められ
[math]
E[H(S)] = \sum_{i=1}^N P(i \in S)
[/math]
と期待値を求めることができました。
設計
[math]E[H(S)] = \sum_{i=1}^N P(i \in S)[/math]の計算に必要な情報は
- 頂点[math]i[/math]の次数[math]\deg i[/math]
- 部分木[math]T_j[/math]のサイズ[math]|T_j|[/math]
になります。
グラフを隣接リストで表現すると次数は簡単に求まります。
部分木のサイズ[math]|T_j|[/math]はDFSで各頂点を再帰的にたどりメモ化すると[math]O(N)[/math]で求めることができます(実装によっては[math]O(N \log N)[/math])。
次に計算量はそれぞれ
- [math]P_B(n_j)=1 – (\frac{1}{2})^{n_j}[/math]は繰り返し二乗法を使うと[math]O(\log n_j)[/math]
- [math]P_0(i) = \prod_{j=1}^k \left(1 – P_B(n_j)\right)[/math]は[math]O(\deg i\log n_j)[/math]
- [math]P_1(i) = \sum_{l=1}^kP_0(i)\cdot\frac{P_B(n_l)}{1-P_B(n_l)}[/math]より[math]P_0(i)[/math]を再利用して[math]O(\deg i\log n_j)[/math]
で求められます。
[math]n_j\leq N[/math]および[math]\sum_i \deg i=2(N-1)[/math]より全体の計算量は
[math]O(\sum_i \deg i\log n_j)=O(N \log N)[/math]
となり間に合うことが分かります。
実装
設計部分と重複しますが
- グラフは隣接リストで表現
- 部分木[math]T_j[/math]のサイズは「頂点[math]i[/math]を頂点[math]j[/math]の親、頂点[math]j[/math]を根とする部分木のサイズ」として頂点ペアをKey、部分木のサイズをValueとしたmapかunordered_mapで記録
とすると良いでしょう。なお、頂点[math]i, j[/math]を入れ替えた場合の部分木のサイズ[math]|T_i|[/math]は[math]|T_i|=N-|T_j|[/math]で求められます。
最後に素数[math]p[/math]を法とする逆元が本問のテーマ[2]素数で割った余りの世界では「割り算」に対応する計算ができます。ですが、より本質的な考察に集中するためにもライブラリを使った方が良いでしょう。例えばAtCoder LibraryのModintライブラリなどが対応しています。
上記を実装したコードはこちらになります。(前半は自作のModIntライブラリで本体は193行目から始まります。)