週記(23/02/26)：アルゴ青コーダへ

今週のまとめ

AHC018は最終37位でフィニッシュ
ABC291バチャ。出てたらかなり冷えてた
ABC292は大当たり回。初黄パフォで青コーダへ

です。まさか今週、青コーダになれるとは思ってなかったので自分でもびっくり。

(本文中にABC291 E, F, JOI 2010予選F, ABC292 C, E, Fの解法を含む話題が出てくるのでご注意ください。)

2/26(Sun)

この日までAHC018に出てました。参加記はこちらで日記編はこちらに書きました。

Tweetを見ていると自分を含めGridを刻んで推定＆探索をした人が多かったみたい。

初めて知ったこと、気づいたこととしては

指定ノードを重み最小で連結にするのは最小シュタイナー木というNP困難な問題
Grid幅は12くらいが良かった
相対スコアなので手元の評価は自己ベスト、理論解との比や[math]C[/math]に比例する傾向があるのでlogを取って評価

あたり。

最小シュタイナー木は前半に調べて分からなくて「まぁNP困難やろ」で進めたけど、知ってたらDP使って解く方法に時間を使っていたはずで結果オーライでした。

Grid幅はVisualizerで見ていると10でも結構粗くて山を通りこしそうになるのでそれより大きい方がいいってのは意外でしたね。

スコア評価は今まであまり意識してなかったのですがAHCも相対評価が定着してきたので評価設計に組み込みたいですね。

2/27(Mon)

朝起きるとシステスが始まってて35位！めっちゃ上がってる！と思ったけどよく見たら上位の人がまだシステス中。

それでも自分より上位で残っているのは2名なので37位に入りそう。

気になって数時間おきに見てしまいます。TLEの場合、3回実行して3回ともTLEならTLEと判定されるみたいですね（知らなかったです）。

今回は3000問 x 上限5秒/問 x 最大3回なので全問TLEだと12時間半かかる計算に。夕方に全問TLEの人の結果がリセットされて(!?)一からやり直しに。

これは今日の結果確定はないなーというのを確認した後はAHCに出てて書けてなかった先々週の週記を書いてアップ。

2/28(Tue)

最終結果が出て37位でした！

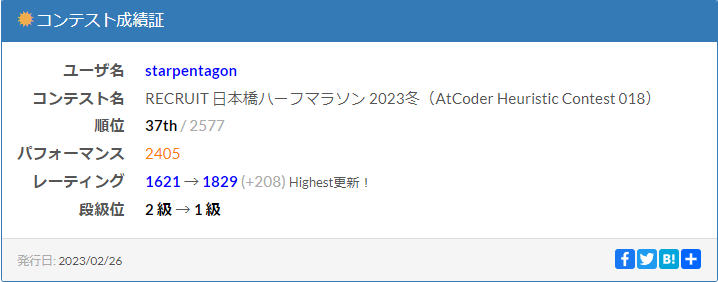
初めての橙パフォ＆商品圏なので素直にうれしいですね。

この日は頑張って参加記を書いてアップ。

最終順位の1つ上がTerryさんでTerryさんの日記みていると

木曜にガウス過程の本を読み始める
その日中にコードを書けるレベルになる(!?)
金曜に1次元ガウス過程で問題を解き始める(!!?)
土曜に2次元ガウス過程で問題を解き始める(!!!?)

で木曜からの動きがすごすぎる…。そして全然違うアプローチなのに相対スコアはほぼ同じというのも面白いですね。

3/1(Wed)

AHCに出ているときはHighになっているのかあまり疲れを感じないのですが、終わるとドッと疲れがでてまだ疲れを引きずっています。

日記編を書いてました。長い…。

3/2(Thr)

日記編を書き上げてアップ。振り返ると考察の積み上げはあるものの進捗の大半はラスト2日で出ているのでもう少し早く進捗を出せるようにしたいですね。

特に序盤に距離Dの点をランダム生成したのは筋悪でしたね。最初からGridにしておけばよかった…。

ABC291のバーチャル参加

ヒューリスティックコンが続いてABCは1か月以上出てなくて久しぶりにバチャ。76分5完(2ペナ)でパフォーマンス1198と出てたらかなり冷えてました。

Eが緑DiffでFが水Diffですか…。AHCに出ている間にアルゴの力が落ちている and/or アルゴ勢強くなっている気がします。

Dまではすんなり解けて「E – Find Permutation」へ。

順序性を有向グラフで表現してトポロジカルソートして考えるところまでは良かったのですが、「一意に特定」の条件を最初パスグラフが作れると思ったけどWA。

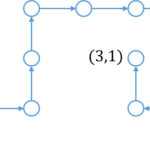
確かに上図だとパスグラフではないですが順序を一意にできます。そうか、始点からすべてのノードに到達可能かを見ればよいのか…で出すとWA。

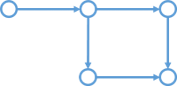
うーん、まじかーと考えると確かに反例があって上図は始点からすべてに到達可能ですが順序を決められないノードがあります。（四角形の左下と右上のノード）

要は全順序を作れるか？って話なのでやっぱりパスグラフが必要でトポロジカルソート順にパスグラフになっているか？を判定してAC。

解説見たら次数0のノードから数字を決めていってそのノードを除去。次数0のノードが複数あったら一意じゃないで確かにこっちのほうがシンプルだった。

Eに時間がかかってバチャ中はここまで。Fも考えたけどよくわからず。

3/3(Fri)

「F – Teleporter and Closed off」は考えたもののなぜかTLEで結局解説AC。ノードの隣接関係が特殊でノード[math]k[/math]に対して

親になりうるノードは[math]k-M[/math]から[math]k-1[/math]
子になりうるノードは[math]k+1[/math]から[math]k+M[/math]

のそれぞれ[math]M[/math]通りしかないのでノード1, Nからの最短路を出しておけば[math]k[/math]を経由しない最短路は[math]O(M^2)[/math]で出せて十分間に合います…と。

問題固有の構造をうまく使えるようにならないとダメですねぇ。

夜は久々に40分ほどジョグ。この冬は競プロというインドアな趣味でだいぶんと運動量が落ちたので少しずつ戻していかないと。

3/4(Sat)

以前解けなかった問題の復習でJOI 2010予選「F – JOI 旗」を解きました。

BitDPですが計算量を[math]3^N[/math]から[math]2^N[/math]に落とすのがまず大変。落とした後もメモリ制限の256MBがキツくてM x N配列で持っていたのを2 x N配列にして、それでもダメで1 x 2にして何とか通りました。これを解く高校生がいるというのはすごい。

ABC292の参加

ヒューリスティックコン参加中はABCには出ていないので1か月ぶりの参加。

最近のABCでうまくいくパターンは1時間くらいでEまで解けてFを最後ギリギリ通すのですがこの日はなんと46分でFまで通せて初の黄パフォ＆入青することができました。

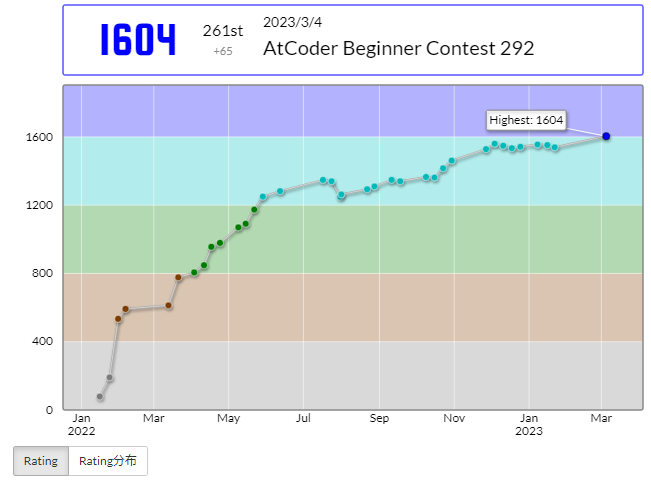
今年に入ってから本番、バチャ含めてほとんど1400-1500パフォだったのでかなりの上振れを引いたと思います。実力的にはまだまだですが、最大瞬間風速的にでも青に行けたのは良い記念なので来週中に色変記事でも書こうかと思います。

「C – Four Variables」は結構難しい。[math]n (1\leq n < N)[/math]について[math]XY=n[/math]の個数cnt[n]は約数の個数になります。[math]N[/math]未満の約数を列挙して[math]\sum_n {\rm cnt}[n]{\rm cnt}[N-n][/math]を計算。

「E – Transitivity」はサンプルを見ながら考えると最終形のグラフは各ノードから遷移可能なノードに辺を張ったグラフになり元のグラフとの差分を出せばOK。

「F – Regular Triangle Inside a Rectangle」は珍しく？数学問。

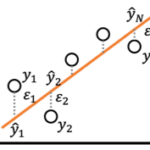
正三角形の頂点の一つは長方形の角にあるとして良く、さらにもう一点は辺上にあるとして大丈夫です。[math]\theta[/math]を上図のようにおくと[math]\theta[/math]に関して

三角形の辺の長さは単調増加
[math]P[/math]のx座標は単調増加
[math]Q[/math]のx座標は単調増加, y座標は単調減少

と単調性があるので点P, Qが長方形内にあるという条件で二分探索しました。

本番中は「え？こんなにきれいな単調性ある？？」思いながらJupyter notebookで確認して、サンプルが1つしかないのでドキドキしながら出しました。

終わった時は「久しぶりにFまで解けた～」しか思ってなくて成績証を見てびっくり。

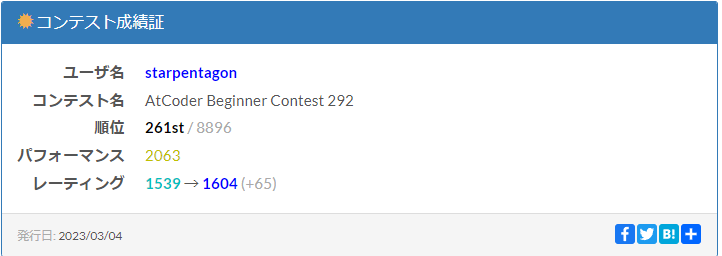
40代にも近づくと仕事でも趣味でも褒められる機会は減ってくるし、体力・気力とも徐々に衰えてくるのですが競プロはレーティングという分かりやすい指標で実力を測れ達成感を得やすいですね。

もちろんレーティング向上だけを楽しみにすると段々辛くなってくると思うので純粋に問題を解く楽しさとかコミュニティのわちゃわちゃ感？を楽しむ方向にもシフトしていきたいなと思います。

前週の週記: 「RECRUIT 日本橋ハーフマラソン 2023冬(AHC018)日記編」
翌週の週記: 「卒園式」