尤度比検定

日本の統計学の教科書では「正規分布に従う2標本の差の検定」など特定状況に適した検定方法を解説していくスタイルが多いですが、教科書”Statistical Inference“では適用範囲が広く汎用的な手法として「尤度比検定」が最初に紹介されています。

実際、

として知られている検定方法もすべて尤度比検定から導出できます。

尤度比の定義

ここでは、一般的な状況としてあるパラメータ[math]\theta\in\Theta[/math]を持つ分布[math]D(\theta)[/math]に従う無作為標本[math]X_1,\ X_2,\ \dots,\ X_n[/math]を抽出して、パラメータ[math]\theta[/math]についての仮説検定を行うことを考えます。

分布[math]D(\theta)[/math] の確率密度関数を[math]f(x|\theta)[/math]とすると尤度関数[math]L(\theta\ |\ \mathbf{x})[/math]は

[math]
L(\theta|\ \mathbf{x}) = \prod_{i=1}^n f(x_i\ |\ \theta)
[/math]

で与えられます。

ここで、帰無仮説[math]H_0[/math]に対応するパラメータ[math]\theta[/math]の集合を[math]\Theta_0[/math]とおき、尤度比を以下で定義します。

次の統計量

[math]
\lambda(\mathbf{x})=\dfrac{\sup_{\theta\in\Theta_0}L(\theta\ |\ \mathbf{x})}{\sup_{\theta\in\Theta}L(\theta\ |\ \mathbf{x})}
[/math]

を尤度比検定統計量(likelihood ratio test statistic)もしくは単に尤度比と呼ぶ。

尤度比[math]\lambda(\mathbf{x})[/math]は

帰無仮説が正しいとした場合の最大尤度 ÷ パラメータ空間全体での最大尤度

なので「帰無仮説が正しい」という立場が

妥当な場合: 尤度比は[math]1[/math]に近い値
誤りの場合: 尤度比は[math]0[/math]に近い値

になります。

「仮説検定」の将棋プログラムの変更の例で実際に尤度比を出してみましょう。ここでは次の状況を考えます。

変更前と変更後のプログラムで自己対戦を1000局実施
変更後のプログラムが550勝450敗

変更が勝率の改善になったかを確認するため以下の帰無仮説、対立仮説を考えます。

[math]H0[/math]: 勝率の改善につながらなかった[math](\theta \leq 0.5)[/math]
[math]H1[/math]: 勝率の改善につながらなかっとはいえない[math](\theta > 0.5)[/math]

勝率[math]\theta[/math]の対局を1000局対局した場合の勝ち数[math]X[/math]は二項分布[math]B(\theta, 1000)[/math]に従います。[math]550[/math]勝した場合の定数項を除いた^[1]尤度の比を取るので対数尤度の定数部分は無視できます。対数尤度関数は

[math]
\log L(\theta|\mathbf{x})= 550\log\theta+450\log(1-\theta)
[/math]

になり

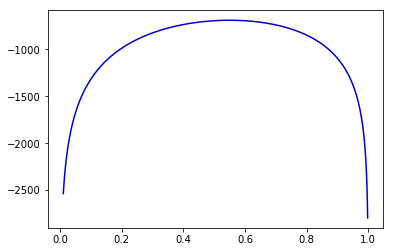
[math]\theta \leq 0.55[/math]で単調増加し[math]\theta=0.55[/math]で最大値を取ります。したがって

帰無仮説の下での最大尤度: [math]L(0.50\ |\ \mathbf{x})[/math]
パラメータ空間全体での最大尤度: [math]L(0.55\ |\ \mathbf{x})[/math]

なので尤度比は

[math]
\lambda(\mathbf{x})=\dfrac{L(0.50\ |\ \mathbf{x})}{L(0.55\ |\ \mathbf{x})}=0.0067
[/math]

と0に近い、つまり帰無仮説は妥当ではなさそうだと分かります。

「帰無仮説が正しい」という立場が誤りの場合に尤度比が0に近い値になることを利用し、尤度比が事前に決めた基準より小さいかどうかで帰無仮説の棄却、採択を決める検定を尤度比検定と呼び、以下の手順で行います。

事前に基準[math]0 < c < 1[/math]を決め棄却域[math]R=\{\mathbf{x}\ |\ \lambda(\mathbf{x})\leq c\}[/math]を設定する。
無作為標本[math]X_1,\dots,X_n\sim D(\theta)[/math]を抽出する。
抽出した標本から[math]\lambda(\mathbf{x})[/math]を計算する。
[math]\lambda(\mathbf{x})\in R[/math]ならば帰無仮説を棄却し、そうでないなら帰無仮説を採択する。

尤度比検定はシンプルですが、有用かつ非常に強力な検定方法であることが知られています。その有用性の一つである十分統計量との関係について紹介します。

「【統計検定対策】十分統計量」で紹介したように最尤推定量を求めるには個々の[math]X_i[/math]ではなく十分統計量と呼ばれる統計量[math]T(\mathbf{X})[/math]さえ分かれば良いことが知られています。さらに十分統計量から求めた尤度比ついて以下が知られています。

[math]T(\mathbf{X})[/math]をパラメータ[math]\theta[/math]の十分統計量とする。[math]\lambda^*(t),\ \lambda(\mathbf{x})[/math]をそれぞれ十分統計量[math]T(\mathbf{X})[/math]および無作為標本[math]\mathbf{X}[/math]から求めた尤度比とする。この時、任意の標本[math]\mathbf{x}[/math]に対し

[math]
\lambda^*(T(\mathbf{x})) = \lambda(\mathbf{x})
[/math]

が成立する。

つまり、十分統計量から求めた尤度比は定義に基づいて求めた尤度比と一致するので、十分統計量から求めた尤度比で尤度比検定が行えることが分かります

なお、証明は[math]g(t|\theta)[/math]を[math]T[/math]の確率密度関数とするとフィッシャー・ネイマンの分解定理から[math]f(\mathbf{x}|\theta)=g(t|\theta)h(\mathbf{x})[/math]とかけることから尤度比が一致することを導けます。