集合論

統計学は確率論をベースに構築されており、確率論は集合論をベースに構築^[1]公理的確率論を理解するには公理的集合論、測度論、ルベーグ積分の理解が必要と言われていますが私の能力を超えているので「Statistical … Continue readingされているためまずは集合論（特に統計学での概念、用語の定義）から始めます。

関心のある実験、状況において起こりうるすべての結果で構成される集合[math]S[/math]を標本空間(sample space)と呼ぶ。

例えば「サイコロを1回振った時の目」の標本空間は[math]S=\{1,2,3,4,5,6\}[/math]になりますし、「6の目が出るまでサイコロを振る回数」の標本空間は[math]S=\{1,2,\dots\}[/math]と自然数全体（可算無限集合）になります。他にも100点満点のテストであれば点数の標本空間は[math]S=\{0,1,\dots,100\}[/math]になりますし、部分点が小数点となる可能性も考慮すると[math]S=\{s\ |\ 0\leq s \leq 100\}[/math]と実数の閉区間（非可算無限集合）なります。

次に事象について定義します。

標本空間の結果の任意の部分集合を事象(event)と呼ぶ。

サイコロの目が偶数になる集合[math]E=\{2,4,6\}[/math]や大学の試験で単位を取り損ねる点数の集合[math]E=\{s\ |\ s < 60\}[/math]は事象になります。

集合演算

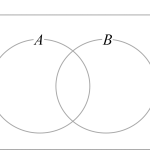
集合[math]A, B[/math]に対する基本的な演算を導入しておきます。

[包含(containment)] [math]A\subset B \overset{\mathrm{def}}{\Leftrightarrow}x\in A\Rightarrow x\in B[/math]
[等号(equality)] [math]A=B \overset{\mathrm{def}}{\Leftrightarrow} A \subset B \ \mathrm{and}\ B \subset A[/math]
[和集合(union)] [math]A\cup B\overset{\mathrm{def}}{=} \{x\ |\ x\in A\ \mathrm{or}\ x\in B\}[/math]
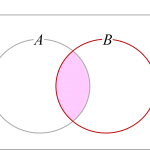
[積集合(intersection)] [math]A\cap B\overset{\mathrm{def}}{=} \{x\ |\ x\in A\ \mathrm{and}\ x\in B\}[/math]
[補集合(complementation)] [math]A^{c}\overset{\mathrm{def}}{=}\{x\in S\ |\ x\notin A\}[/math]

集合演算の基本的な性質として以下が成立します。

[math]A,B,C[/math]を標本空間[math]S[/math]の事象（部分集合）とする。このとき以下の性質が成立する。

[交換律(Commutativity)] [math]A\cup B=B\cup A,\ A\cap B=B\cap A[/math]
[結合律(Associativity)] [math]A\cup (B \cup C)=(A \cup B)\cup C,\ A\cap (B \cap C)=(A \cap B)\cap C[/math]
[分配律(Distribution Laws)] [math]A\cap (B \cup C)=(A \cap B)\cup (A\cap C),\ A\cup (B \cap C)=(A \cup B)\cap (A \cup C)[/math]
[ド・モルガンの法則(DeMorgan’s Laws)] [math](A \cup B)^c=A^c \cap B^c,\ (A \cap B)^c=A^c \cup B^c[/math]

各性質の証明は

交換律: [math]\cup, \cap[/math]の定義が[math]A, B[/math]について対称なので自明
結合律、分配律、ド・モルガンの法則: 定義に従い
- 左辺の要素が右辺の集合に含まれる
- 右辺の要素が左辺の集合に含まれる
ことを示す。

ことでできます。

コルモゴロフの公理的確率論の準備^[2]公理的確率論のキモは可算無限個の事象に対する確率を定義するところでその前準備です。として2つの集合間で定義された和集合、積集合を可算無限個の集合[math]A_1, A_2, \dots\subset S[/math]に拡張しておきます。

[和集合] [math]\bigcup_{i=1}^\infty A_i\overset{\mathrm{def}}{=} \{x\in S\ |\ x\in A_i\ \mathrm{for\ some}\ i\}[/math]
[積集合] [math]\bigcap_{i=1}^\infty A_i\overset{\mathrm{def}}{=} \{x\in S\ |\ x\in A_i\ \mathrm{for\ all}\ i\}[/math]

それぞれ

「少なくとも一つ」の[math]A_1, A_2, \dots[/math]に含まれる結果の集合
「すべて」の[math]A_1, A_2, \dots[/math]に含まれる結果の集合

を意味しており自然な拡張になっています^[3]定義は自然な拡張ですが無限特有の演算の難しさ、結果の理解しづらさがあるので位相の教科書や演習問題にあたることをお勧めします。。無限可算個の集合に対する和集合、積集合についても交換律、結合律、分配律、ド・モルガンの法則が成立することが示せます。

最後に標本空間の分割について定義します。

事象[math]A_1, A_2, \dots\subset S[/math]に対し任意の[math]i\ne j[/math]について[math]A_i\cap A_j=\emptyset[/math]が成立するとき互いに排反(pairwise disjoint or mutually exclusive)であるという。

つまり、どの2つの事象をとっても同じ結果を含まない（ダブりがない）ことを意味しています。例えば「サイコロを[math]k[/math]回目に振ったときに初めて6が出る」という事象を[math]E_k(k=1,2,\dots)[/math]とすると[math]E_k[/math]は互いに排反になります（事象[math]E_k[/math]の定義中の”初めて”というのがポイントで単に「[math]k[/math]回目に6が出る」という定義では排反になりません）。

事象[math]A_1, A_2, \dots\subset S[/math]が互いに排反で[math]\bigcup_{i=1}^\infty A_i=S[/math]のとき、事象[math]A_1, A_2, \dots[/math]は[math]S[/math]の分割(partition)であるという。

要は標本空間をMECEに分けたときの事象を分割と呼びます。「6の目が出るまでサイコロを振る」という標本空間[math]S[/math]は互いに排反な事象[math]E_1, E_2, \dots[/math]を用いて[math]S=\bigcup_{i=1}^\infty E_i[/math]と書けるので事象[math]E_1, E_2, \dots[/math]は標本空間[math]S[/math]の分割になっています。この例から分かるように標本空間を可算無限個の事象（部分集合）で分割するのが自然なケースがあり、この状況でも数学的に整合の取れた理論体系を構築したのがコルモゴロフの公理的確率論^[4] … Continue readingです。

シリーズ記事

統計学
- 1.1 集合論(本記事)
- 1.2 コルモゴロフの公理

参考文献

Casella, G and Berger, R.L.(1990), Statistical Inference(Second Edition): Section 1.1 Set Theory

脚注[+]

脚注
↑1	公理的確率論を理解するには公理的集合論、測度論、ルベーグ積分の理解が必要と言われていますが私の能力を超えているので「Statistical Inference」の構成に沿って整理します。
↑2	公理的確率論のキモは可算無限個の事象に対する確率を定義するところでその前準備です。
↑3	定義は自然な拡張ですが無限特有の演算の難しさ、結果の理解しづらさがあるので位相の教科書や演習問題にあたることをお勧めします。
↑4	応用上、可算無限の範囲まで取り扱うことが必須である一方、可算無限の範囲まで拡張した確率論を正当化するには大学教養レベルを超えた数学が必要になることが確率の難しさの一つだと思います。