THIRDプログラミングコンテスト2022(AHC017)参加記

2023年1月28～2月5日に開催された「THIRDプログラミングコンテスト2022(AHC017)」で165位になり晴れて青コーダになれました！

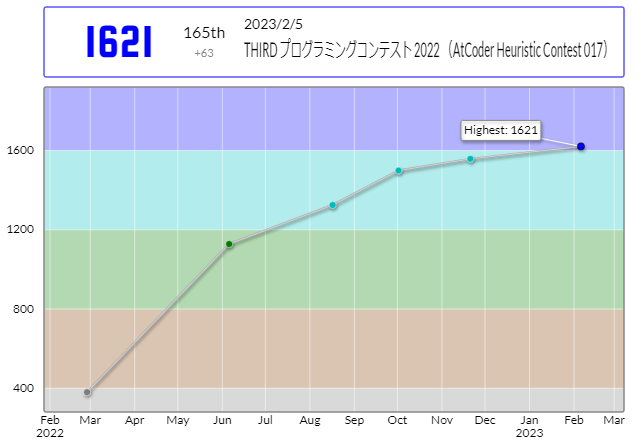
初期解の構築に力を入れ過ぎて高速化に手が回らずスコアを伸ばせなかったのは残念ですがギリギリまで粘って最終日に順位上げて青パフォ圏に入れたのは良かったです。

提出解法の紹介と終了後のTweetを参考にこうすればよかったという振り返りを行いたいと思います。

なお、本記事は提出解法というある意味「上澄み」部分だけ触れています。試行錯誤や産みの苦しみ？を味わう過程は日記編見ていただければと思います。

コンテスト／問題概要

[math]N (500 \leq N \leq 1000)[/math]頂点, [math]M (500\leq M \leq 3000)[/math]辺の平面グラフが与えられます。[math]D(5\leq D \leq 30)[/math]日間で各辺を1回通行止めにして工事を行い、工事により各点からの最短距離の総和が増えた分を不満度とします。

1日最大[math]K (5\leq K \leq 30)[/math]辺の工事ができる時、不満度を最小化する工事のスケジュールを求める問題になります。

提出解法

一日平均での工事辺数[math]\lceil M/D \rceil[/math]と[math]K[/math]の大きさでアルゴリズムを使い分けました。

スケジュールが厳しくない場合([math]K > \lceil M/D \rceil + 7[/math])

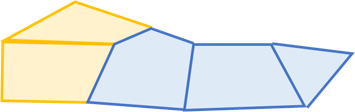
まず重要な考察として工事する辺には「相性」があり単独で工事するより同時に工事した方が不満度の合計が小さくなることがあります。

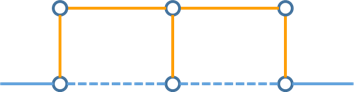
上図で点線の辺を工事するとオレンジの迂回路になりますが、別々の日に行うと2回迂回が必要になるのに対し同時に行うと1回で済むため不満度を減らすことができます。

特に各点からの最短路によく使われる辺の工事日をまとめられると大きく不満度を下げることができます。

ただし、まとめて工事した結果、非連結になると大きな不満度が発生するので連結性を保ちつつ最短路によく使われる辺をまとめて工事できるかがポイントになります。

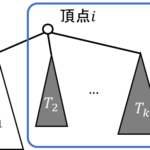
まず各点から最短路木を作った時に辺[math]e[/math]を通った回数[math]E_e[/math]^[1]Edge betweennessと呼ばれコミュニティ抽出で良く用いられます。を求めておきます。

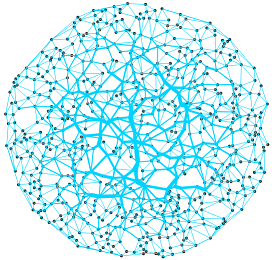
[math]E_e[/math]の大きさに応じて辺を塗り分けると目の網膜？みたいになります。[math]E_e[/math]が大きい辺[math]e[/math]を同時に工事すると全体の不満度を下げることが期待できます。

次に大きな[math]E_e[/math]を含む面を一定の大きさまでつなげます。面集合をうまく作ると

• 連結性を保てる^[2]面集合の中で辺数の小さいものから工事する日を決めていき、未決定の辺が[math]D[/math]個以下なら連結性を保てます。
• 迂回路の大きさを抑えられる^[3]面を構成する辺は一辺を工事した場合の迂回路の１つになります。大きさを制限することで極端に大きな迂回路を作らないようにできます。

ことを保証できるので値[math]E_e[/math]が大きいもの同士を同じ日に割り当てて初期解とします。

この後は山登り法で改善しました。遷移は「辺を1つ決めて別の工事日にする」で反復回数が少ない時は[math]E[/math]が大きいものを優先し、徐々にランダムにしました。

スケジュールが厳しい場合([math]K \leq \lceil M/D \rceil + 7[/math])

上記の方法で[math]K[/math]に制限がなければ連結性を保てるのですが[math]K[/math]が厳しいと初期解を修正した際に非連結な成分が出てしまうことがありました。

この場合は[math]D[/math]個の全域木を

「使わない辺の和集合が辺全体になる」

ように決めて、その全域木は工事しないようにしました。

振り返り

参加中の試行錯誤は改めて日記編として残したのでそちらをご覧ください。ここでは他の参加者の方の解法を参考にこうしておけば良かった…と振り返りたいと思います。

不満度計算の代替指標の見極め

不満度を真面目に計算すると[math]O(DN(N+M)\log N)[/math]かかるため数回計算するだけで6秒を使い切ってしまいます。

時間を稼ぐ方法として

• 高速化する(最短路木を差分計算する)
• 計算する点を間引いて近似計算する

などが必要でした。

ただ、私は序盤に可視化してEdge betweenness [math]E_e[/math]が使えそうというアイディアに惚れて？しまって最終盤まで代替指標として使っていました。

ただ、辺の相性を測るには良くても正確なコストとの相関が低くて代替指標として使えない…という悲しい事実に最後の最後で気づいて方針転換を余儀なくされました。

ラスト数時間で点を間引こうと思って試したのですが、時間制限を付けて回すとスコアが落ちたため変更する辺の端点について計算するのが精一杯でした。

不満度を最小化する構造の見極め

辺の「相性」に気づいて考察、ロジック化できたのは良かったのですが同時に工事する辺をパスグラフのようにつなげると良い解になりやすかったようです。

AHCラジオでも触れられて^[4]29分ごろに触れられています。いますが山登り法で1時間くらい放置するとそういった構造の解が選ばれていたようで

愚直解法を長時間回して解の性質、特徴を観察する

という基本をきちんとすべきだったと思います。

時間配分

少し言い訳になってしまうのですが社会人だと平日夜にがっつりコーディングする元気が残っていなくて、可視化＆考察で進捗を生んだ気になっていました。

初期解構築が勝負と思い込んで実装してみたものの初期解から山登り法でどんどん良くなり、本当はその先の高速化が勝負でした。

手数が少なかった分、勝負ポイントを外してしまったと反省です。

感想

最短路がテーマで序盤はこの問題固有のコーディングがほとんどなく実装が軽いなーと思っていましたが、考察すればするほど問題の性質が見えて実装の沼にはまり込んでいきました。

反省点は色々あるものの可視化＆考察した内容をロジックに落としこんでうまく行くとやはり嬉しいですし、青コーダになれた記念の回になりました。

今回も1週間ちょっとどっぷりと楽しめました。スポンサーのTHIRDさん、作問者のwataさん、参加者の皆様ありがとうございました。

復習＆延長戦(2023/02/11追記)

TweetやAHCラジオを参考に復習＆気になる点を改善していました。

一番大きかったのはymatsuxさんの「THIRD プログラミングコンテスト (AtCoder Heuristic Context 017): 20位以内のスコアを出すシンプルな解法」で紹介されている最短路木の差分計算です。

本番では2点での評価が精一杯でしたが9点評価にしたうえで20-30倍（！）速くなりました。この高速化で平均13.9Mあった不満度が9.9Mに減り相対スコアも40.4Gへ。

あとはAHCラジオで紹介されていた「辺の工事日を変える際に隣接する辺と工事日を合わせる」を入れると平均不満度が9.6M、相対スコア42.3Gまで伸びました。

観察で得られた特徴(一直線にまとめて工事すると良くなりやすい)をうまくロジックに落とし込めてますね。これを本番で出来ていたら気持ちいいだろうなぁ。

あと高速化で劇的に良くなったのでやはり「速いは正義」ですね。最短路木の差分計算は使う機会がありそうなのでその時はうまく使いたいですね。