2018年6月開催分の解答例です。前回に続き今回も仮説検定や区間推定からの出題が多くありました。内容も
- 定義を正確に暗記
- 統計量等を正確に算出
- 算出結果を適切に評価
できることが要求されており難度が高いです。今後もこの傾向が続きそうなので受験される方はきちんと準備をしておいた方が良さそうです。
なお、他の開催分の解答例はこちらを参照ください。
問1
[1]偏差が「平均からの差」、標準化得点が「平均0、分散1に正規化した値」であることと縦軸の範囲が
- -2~2
- -20~30
- 30~80
であることから総得点: III, 偏差: II, 標準化得点: Iが対応し「5」が適切。
[2]平均から標準偏差の2倍以上離れた観測値の範囲は
- [math]54.45-11.77\times 2 = 30.91[/math]以下
- [math]54.45+11.77\times 2 = 77.99[/math]以上
なので「名古屋」のみ該当し「2」が適切。
問2
[3]各記述は
- 散布図で右斜め方向に分布しており「正」
- 相関係数は外れ値の影響を受けやすく「正」
- 正の相関が見られるため「誤」
[4]各記述は
- 北海道は同程度の人口の都道府県と比べ一般病院病床数が多く「誤」
- 人口にほぼ比例しているため人口1当たりの一般病院病床数の変動係数は一般病院病床数の変動係数より小さくなることが想定され「正」
- 人口上位の9都道府県も正の相関関係が見られるため「誤」
なお、IIがわからなくてもI, IIIが明らかに誤のため「5」に絞り込めます。
[5]各記述は
- 偏相関係数の説明として「正」
- 擬相関が疑われ「正」
- この結果から映画館の併設についてはわからず「誤」
この問題もIがわからなくてもII, IIIがわかれば正解を「1」絞り込めます。
問3
[6]人口の累積相対度数ごとに第[math]n[/math]五分位階級の累積値を描いたのがローレンツ曲線です。図より人口累積度数が[math]80\%[/math]のときに所得の累積相対度数が[math]60\%[/math]の国を探すと「5(ドイツ)」が適切。
[7]ジニ係数は下図の[math]A/(A+B)[/math]もしくは[math]2A(\because A+B=0.5)[/math]なので面積を求めると「2」が適切。
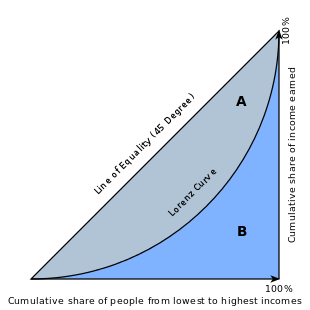
Wikipedia: 「ジニ係数」より
[8]各記述は
- すべての国のローレンツ曲線は完全平等線の下を描き「正」
- 日本、アメリカ、ドイツの中ではアメリカが第1~4五分位階級の値が小さく、第5五分位階級の値が最も大きい。これよりローレンツ曲線が一番下を描いておりジニ係数は大きいため「誤」
- スウェーデンと中国では中国の方がローレンツ曲線が一番下を描いておりジニ係数は大きいため「正」
問4
[9]変化率は[math]\dfrac{87.5-89.5}{89.5}=-2.2\%[/math]
[10]条件より[math]89.5\times (1+r)^5=100[/math]なのでこれを[math]r[/math]について解くと「2」が適切。
問5
[11]フィッシャーの3原則(繰り返し、局所管理、無作為化)より「2」が適切。
問6
[12]男女のように層別し層の比率を揃えて標本を抽出する方法を「層化抽出」と呼び「5」が適切。
問7
[13]S君がお菓子をもらえるのは
- T君、U君に2連勝: [math]pq[/math]
- T君に負けた後、U君、T君に連勝: [math](1-p)qp[/math]
なので「5」が適切。
[14]
- 「T君-U君-T君」の対戦順でお菓子がもらえる確率: [math]P_1[/math]
- 「U君-T君-U君」の対戦順でお菓子がもらえる確率: [math]P_2[/math]
とすると[13]と同様の計算から[math]P_2=qp+(1-q)pq[/math]なので
[math]
\begin{eqnarray}
P_1 – P_2 &=& (1-p)qp – (1-q)pq \\
&=& pq(q-p) \\
&>& 0
\end{eqnarray}
[/math]
より常に「T君-U君-T君」の対戦順の方がお菓子をもらえる確率が高く「1」が適切。
問8
[15][math]X[/math]を標準化して
[math]
\begin{eqnarray}
&& P(X \geq 4800) \\
&=& P\left(\frac{X-4000}{500} \geq \frac{4800-4000}{500}\right) \\
&=& P(Z \geq 1.6) \\
&=& 0.055
\end{eqnarray}
[/math]
なので「2」が適切。
[16]6月およびその前年6月の電気料金を[math]X, Y\sim \mathcal{N}(4000, 500^2)[/math]とすると[math]X-Y\sim\mathcal{N}(0, 2\times 500^2)[/math]より
[math]
\begin{eqnarray}
&& P(X-Y \geq 800) \\
&=& P\left(\frac{X-Y}{500\sqrt{2}} \geq \frac{800}{500\sqrt{2}}\right) \\
&=& P(Z \geq 1.13) \\
&=& 0.129
\end{eqnarray}
[/math]
なので「3」が適切。
[17]
ある年、前年、前々年の6月の電気料金を[math]X_1, X_2, X_3[/math]とする。大小順は6通りあり[math]X_i[/math]は独立なのでそれぞれ同様に確からしく起きる。よって[math]X_1[/math]が最も高くなるのは大小順6通り中2通りあり確率は[math]1/3[/math]より「2」が適切。
問9
[18][math]E[X^2]=V[X]+E[X]^2[/math]および[math]Cov[X,Y]=E[XY]-E[X]E[Y][/math]を用いて計算すると「4」が適切。
[19][math]E[U], E[V], E[UV], V[U], V[V][/math]を求め[math]Cov[U, V], r[U,V][/math]を計算すると「4」が適切。
問10
[20][math]\bar{X}\sim \mathcal{N}(\mu, 1/n)[/math]なので
[math]
\begin{eqnarray}
&& P\left( \frac{|\bar{X}-\mu|}{1/\sqrt{n}} \leq 0.5\sqrt{n} \right) \geq 0.95 \\
&\Leftrightarrow& P(Z \leq 0.5\sqrt{n}) \geq 0.95 \\
&\Leftrightarrow& 0.5\sqrt{n} \geq 1.96 \\
&\Leftrightarrow& n \geq 15.3
\end{eqnarray}
[/math]
なのでこれを満たす最小の[math]n[/math]は[math]16[/math]で「4」が適切。
[21]
母平均[math]\mu[/math]の[math]95\%[/math]信頼区間は
[math]
\bar{X}-t_{n-1,\alpha/2}\sqrt{\frac{S^2}{n}}\leq \mu \leq \bar{X}+t_{n-1,\alpha/2}\sqrt{\frac{S^2}{n}}
[/math]
なので「1」が適切。
問11
[22]母比率の[math]95\%[/math]信頼区間は
[math]
\hat{p}-z_{\alpha / 2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \leq p \leq \hat{p}+z_{\alpha / 2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}
[/math]
で与えられるので「3」が適切。
[23]
北海道と沖縄の野球の行動者数は[math]N_1\hat{p}_1+N_2\hat{p}_2[/math]で北海道と沖縄の人口は[math]N_1+N_2[/math]なので母比率の推定値は[math]\dfrac{N_1\hat{p}_1+N_2\hat{p}_2}{N_1+N_2}[/math]である。推定値の分散を計算すること、もしくは選択肢1が不適当なことから「2」が適当。
問12
[24]まずセリーグ、パリーグの不偏分散を求めると[math]s_c^2=13549/(6-1)=2709.8[/math], [math]s_p^2=7763/(6-1)=1552.6[/math]である。2標本をプールした分散を求めると
[math]
s^2 = \dfrac{(6-1)s_c^2+(6-1)s_p^2}{(6-1)+(6-1)}=2131.2
[/math]
なので[math]t=\dfrac{233.7-185.3}{\sqrt{s^2(1/6+1/6)}}=1.82[/math]を得る。よって「4」が適切。
[25]
12球団全体の平均は[math](233.7+185.3)/2=209.5[/math]であり、リーグによる平方和は
[math]
\begin{eqnarray}
&& (233.7-209.5)^2\times 6 \\
&&\quad +(185.3-209.5)^2\times 6 \\
&=& 7027.68
\end{eqnarray}
[/math]
である。また、残差平方和(自由度10)は[math]13549+7763=21312[/math]より[math]F=7027.68/2131.2=3.30[/math]なので「4」が適当。
問13
[26]検定Iの棄却域は[math]X \leq 3[/math]なので
- 第一種の過誤: 帰無仮説が正しいのに帰無仮説を棄却としてしまう確率、つまり[math]0.3[/math]
- 第二種の過誤: 対立仮説が正しいのに帰無仮説を棄却しない確率、つまり[math]0.1[/math]
- 検出力: 1-「第二種の過誤」、つまり[math]0.9[/math]
より「4」が適切。
[27]検定IIの棄却域は[math]X \leq 2[/math]なので
- 第一種の過誤: 帰無仮説が正しいのに帰無仮説を棄却としてしまう確率、つまり[math]0.2[/math]
- 第二種の過誤: 対立仮説が正しいのに帰無仮説を棄却しない確率、つまり[math]0.3[/math]
- 検出力: 1-「第二種の過誤」、つまり[math]0.7[/math]
であり、検定IIIの棄却域は[math]X=6[/math]なので
- 第一種の過誤: 帰無仮説が正しいのに帰無仮説を棄却としてしまう確率、つまり[math]0.3[/math]
- 第二種の過誤: 対立仮説が正しいのに帰無仮説を棄却しない確率、つまり[math]1.0[/math]
- 検出力: 1-「第二種の過誤」、つまり[math]0.0[/math]
となる。これより「2」が適切。
問14
[28]失業率、[math]\log[/math](賃金)、[math]\log[/math](警察官数)の値を代入すると[math]\log[/math](犯罪発生率)は[math]6.4[/math]となり「5」が適切。
[29]
統計量[math]T=\frac{\beta_3 – \hat{\beta}_3}{{\rm Std. Error}}[/math]は自由度[math]n-k-1[/math]の[math]t[/math]分布に従う。ここで[math]\hat{\beta}_3[/math]は帰無仮説での[math]\beta_3[/math]の値で[math]k[/math]は説明変数の数である。これより
[math]
T=\dfrac{-0.06498-(-0.5)}{0.22718}=1.91
[/math]
である。自由度は43なので自由度[math]40(\approx 43)[/math]の[math]t[/math]分布表から
[math]
t_{0.05}(40) = 1.684 < T < 2.021 = t_{0.025}(40)
[/math]
なので両側検定であることに注意すると有意水準[math]5\%[/math]だと棄却されず[math]10\%[/math]だと棄却されるので「4」が適切。
[30]各記述は
- Pr(>|t|)が0.01より小さい回帰係数は2つあり「正」
- [math]\log[/math](賃金)の回帰係数が正であり[math]\log[/math]は単調増加するので賃金が高くなると犯罪発生率も高くなり「誤」
- Adjusted R-squaredの値は0.5787となっており「正」
なので「4」が適切。
問15
[31]365日中120日が冬季で風向が北の日が207日あるので期待度数は[math]120 \div 365 \times 207=68.05[/math]である。
[32]独立性検定の[math]\chi^2[/math]統計量は「実測値と期待値の差の二乗」を「期待値」で割ったものの「総和」なので「2」が適切。
[33][math]\chi^2[/math]統計量は自由度[math](2-1)\times (2-1)=1[/math]の[math]\chi^2[/math]分布に従い上側[math]5\%[/math]点の値は[math]3.84[/math]である。統計量の値は[math]69.04[/math]なので棄却され「5」が適切。
問16
[34]等分散性検定の統計量[math]F[/math]を求めると
[math]
F = \dfrac{19.5^2}{14.5^2}=1.81
[/math]
で両側検定なので付表から[math]F_{0.025}(20,40)=2.068 > 1.81[/math]より棄却されず「2」が適切。