週記(23/04/09)：幻の水青反復

今週のまとめ

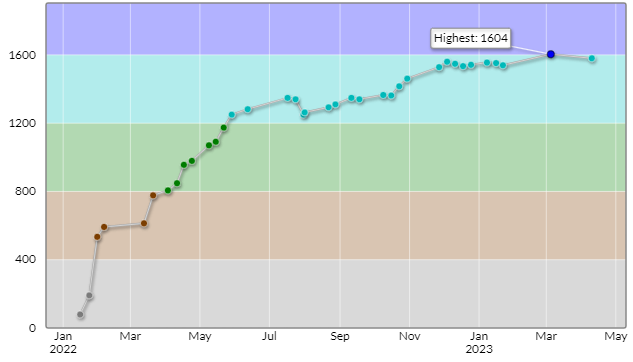
ABC297参加。水色に戻る
ABC295バチャ。出てたらかなり冷えてた
ABC298参加。幻の青復帰

です。

(本文中にABC 080D, 081D, 296D-E, 297D-F, 298 E-Fの解法を含む話題が出てくるのでご注意ください。)

4/9(Sun)

ABC297の参加

62分5完パフォーマンス1339で水色に逆戻りでした。

今のレートだとEまでの早解き勝負でFは間に合いそうもなかったので仕方ないですね。

「D – Count Subtractions」はちょっと考えて再帰関数で書くと

[math]f(a,b) = \lfloor b/a \rfloor + f(a, b\ \% \ a)[/math]

でユークリッド互除法と同様の形で計算量は[math]O(\log \max(a,b))[/math]で間に合います。

「E – Kth Takoyaki Set」は二分探索とちょっと迷いましたが一度DPで考えて

dp[i][m]: i種類目までのたこ焼きで金額mにできるか

とすると

dp[i+1][m] |= dp[i][m]
dp[i+1][m+[math]A_{i+1}[/math]] |= dp[i+1][m]

になります。[math]K[/math]個目まで分かればよいのと金額は大きな値になりうるのでsetで管理して

i番目まで使った時の実現可能な金額を小さい順にK個持っておく
i+1番目はi番目の結果mを小さい順に取り出しつつm+[math]A_{i+1}[/math]を加えた値を追加しながらK個まで取る

と更新しておけばOKです。

この日は走りに行く時間はなく筋トレをして終了。

4/10(Mon)

「F – Minimum Bounding Box 2」をupsolve。

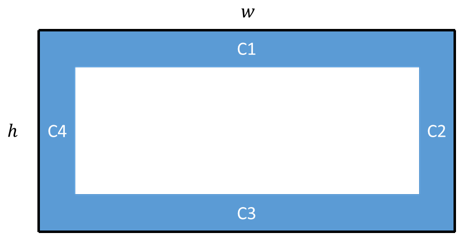
方針はサイズ[math]h \times w[/math][math](h \in [1, H], w \in [1, W])[/math]の長方形が最小長方形になる場合の数を数え、スコアの期待値を求めます。

[math]hw[/math]個のグリッドに[math]K[/math]個のマスを選ぶ場合の数は[math]{}_{hw}C_{K}[/math]個あります。ただ、

[math]C_1,\dots,C_4[/math]の各領域に1つもマスがない場合は最小性に反してしまうのでその場合の数を除く必要があります。

事象[math]E_i[/math]を「領域[math]C_i[/math]にマスが0個」としてその場合の数を[math]n(E_i)[/math]と書くと除く場合の数は[math]n(E_1 \cup E_2 \cup E_3 \cup E_4)[/math]になり包除原理でAND条件で書き直します。

そうすると各場合の数は長方形から[math]C_i[/math]を除いた領域に[math]K[/math]個のマスがある場合の数として出すことができます。

あとはこの場合のスコア[math]hw[/math]をかけて、この長方形の取り方が[math](H-h+1)(W-w+1)[/math]通りあるのを使えば期待値を出せます。

[math]n \geq 3[/math]の包除原理は初めて使いましたが、OR条件だと重複の扱いが難しいですが包除原理でAND条件にすると数え上げやすくなることが良く分かる好例ですね。

本番は必ず4隅にマスが少なくとも2つはある…と考えてしまってて終わってから間違いに気づきました。実力不足で仕方ないな…という感じです。

4/11(Tue)

水Diffの練習でABC080「D – Recording」を解きました。

あれ？Imos法で終わり？と思ったらWA。

別チャンネルだと録画開始前に0.5秒必要というのは、同じチャンネルだと準備時間は不要というのを理解してませんでした。読解力不足。

同じチャンネルで連続するものを前処理でマージしましたが、解説を見るとImos法で増減を出して同じチャンネルは+2を+1にするというやり方が簡明でした。

この日は1時間ほどランニング。日曜の筋トレの筋肉痛でちょっとしんどい。

4/12(Wed)

水Diffの練習でABC081「D – Non-decreasing」を解きましたが時間がかかった！

1時間かけても解けずそこからさらに1時間近く粘ってようやくAC。

最初は2N回という制約から「a_{i-1} > a_i」ごとに2回操作して非減少にできないか？と考えて最大、最小を足したりするのを考えましたが、一度非減少にしても隣の要素を操作したときに非減少が崩れることがあり断念。

次に非減少⇔階差列が0以上なので階差列を操作できないか？と考えましたがこれも同様の問題が発生して断念。

結局、順に決めるしかないと思い最大、最小の絶対値で場合分けして

最大の絶対値が大きい場合は前から
最小の絶対値が大きい場合は後ろから

順に決めていくことに。

前者の場合は小さい方に最大を足し、後者の場合は大きい方に最小を足していけば高々2回で非減少にできますが、無邪気に全要素に2回操作するとオーバーフロー…。必要なところだけ操作するようにしてようやくAC。

要素数が最大50なのと値が10^6程度なのに助けられた気がします。

解説を見るととても賢くて

仮に数列の各要素が 0以上 or 0以下なら累積和で非減少列を作れる
最大値の絶対値 > 最小値の絶対値なら最大値を足すことで0以上にできる
最大値の絶対値 < 最小値の絶対値なら最小値を足すことで0以下にできる

を合わせて非減少列を作れます。これは構築系の典型として押さえておきたいですね。

4/13(Thr)

ABC295のバーチャル参加

ABC296バチャに続いて3完、パフォーマンス957相当。いやーアルゴは不調ですね。

「D – Three Days Ago」は最初、

数字ごとに各位置で出現回数が偶数かのbitをもつ
位置[math]l[/math]での各数字のbitのANDをとる
[math]l[/math]以降で1の個数を求める

でOKと思ったのですがTLE。

[math]2^{10}|S|\leq 5\times 10^8[/math]でギリ間に合うハズと定数倍高速化をしているうちに終了。

お風呂に入りながら考えるとSのlからr文字目が「嬉しい列」になる必要十分条件は

位置[math]l-1[/math]での各数字の偶奇と位置[math]r[/math]での各数字の偶奇が一致

で各数字の出現回数の偶奇で同値類を作ってその中から2つ選ぶ場合の数を出してAC。

条件を満たす区間を数える問題で同値類を作ってそこから選ぶ場合の数に帰着するのは時々見ますがこれが緑Diffとはマジかーという感じ。レベル高い。

4/15(Sat)

ABC295「E – Kth Number」をupsolve。これも難しい。

順序統計量の分布が分かればよいので昔書いた「順序統計量」を見ながら解きました。

方針としては[math]x\in [1,M][/math]を固定して[math]P(A_K \leq x)[/math]を求めます。[math]A_i \ne 0[/math]の要素は固定なのに注意して未確定の個数を[math]C[/math], 確定した値のうち[math]x[/math]以下の個数を[math]L(x)[/math]とします。順序統計量の定石で確率変数[math]Y[/math]を「未確定の要素が[math]x[/math]以下になる個数」とすると

[math]P(A_K \leq x)=\sum_{k=K-L(x)}^C P(Y=k)[/math]

になり

[math]P(Y=k)=\dfrac{ {}_{C}C_k x^k (M-x)^{C-k} }{M^C}[/math]

から出せます。計算量は[math]x[/math]が[math]M[/math]通り、[math]P(A_K \leq x)[/math]が[math]O(N\log N)[/math]なので全体[math]O(MN\log N)[/math]で十分高速です。

ABC298の参加

62分6完で361位！すぐに青復帰！！と思いきやUnratedでした…。残念ですがDDoS攻撃で接続できない人がいたなら仕方ないですね。

「E – Unfair Sugoroku」はメモ化再帰でサクッと解けました。[math]f(t, a, b)[/math]を

手番が高橋君([math]t=0[/math]) or 青木君([math]t=1[/math])でそれぞれ位置a, bにいる時の高橋君の勝率

とすると高橋君が手番の時は

[math]f(t,a,b) = \dfrac{1}{P}\sum_{p=1}^P f(1-t, a+p, b)[/math]

で青木君も同様の式が成立し、状態数、遷移数も多くないので間に合いますね。

「F – Rook Score」は面白い問題でした。

行、列番号の値が大きいので座標圧縮しておきます。列を順にみていくとその列に対して総和が最大になる行は「行合計から該当列を引いた数列」で最大のものになります。

これをセグ木で管理して「該当列を引く」操作は全体で[math]N[/math]回なので全体[math]O(N \log N)[/math]になります。

前週の週記: 「色変記事」
翌週の週記: 「Euler Tour」