【統計検定対策】モーメント母関数による確率密度関数の導出

確率変数 $X$ のモーメント $E[X^n]$ の算出でよく用いるモーメント母関数ですが、確率密度関数の導出でも活躍します。2016年に出題された問題を例に見てみましょう。

2016年（数理統計）の大問2(4)で

指数分布(

$\lambda>0$ )に従う独立な確率変数

$X_1,\dots,X_n$ に対し、

$Y=\sum_{i=1}^n X_i$ とする。

$Y$ の確率密度関数は

$g_n(y)=\begin{cases}\dfrac{\lambda^n}{\Gamma(n)}y^{n-1} e^{-\lambda y} &(y\geq 0) \\ 0 &(y<0)\end{cases}$ となることを示せ。

という問題が出題されました。数学的帰納法を使って示すこともできますが、

が一致することを示すことで $Y$ の確率密度関数が $g_n(y)$ になることを示せます。その根拠となるのが以下の定理です。

確率変数

$X, Y$ の確率密度関数をそれぞれ

$f_X(u), f_Y(u)$ とし、モーメント母関数

$M_X(t), M_Y(t)$ が存在するとする。

$M_X(t)=M_Y(t)$ ならば、

$f_X(u)=f_Y(u)$ である。

つまりモーメント母関数が一致することを示すことで確率密度関数の一致を示せます。図示すると以下の関係になります。

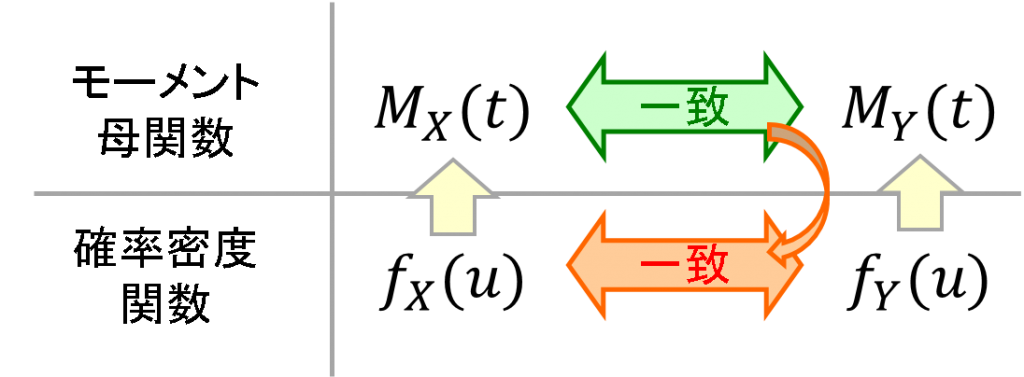
この定理を使って過去問を解いてみましょう。

まず、指数分布のモーメント母関数を求めると

$M_{X_i}(t)=E[e^{tX_i}]=\dfrac{\lambda}{\lambda-t}$

になります。これより、

$\begin{eqnarray} M_{Y}(t)&=&E[e^{t\sum_{i=1}^{n}X_i}]\\ &=&\prod_{i=1}^nE[e^{tX_i}] \\ &=&\left(\dfrac{\lambda}{\lambda-t}\right)^n \end{eqnarray}$

になります。

次に $g_n(y)$ のモーメント母関数を求めます。
まず $g_1(y)$ は指数分布の確率密度関数に他ならないので $M_{g_1(y)}(t)=\dfrac{\lambda}{\lambda-t}$ です。
さらに部分積分を使うことで

$M_{g_n(y)}(t)=\dfrac{\lambda}{\lambda-t}M_{g_{n-1}(y)}(t)$

なので

$M_{g_n(y)}(t)=\left(\dfrac{\lambda}{\lambda-t}\right)^n$

が得られます。

以上より

$M_Y(t)=M_{g_n(y)}(t)$

なので $Y$ の確率密度関数は $g_n(y)$ に一致することが示せました。