【統計検定1級過去問】2015年（統計数理）大問2 解答例

コメント

大問2は仮説検定の検出力に関する問題が出題されました。内容は

• P値
• 検出力
• 一様最強検出力検定（ネイマン・ピアソンの補題）

と特に奇をてらったものはないですが、いずれも問題文中に定義が与えられておらず

覚えていなければ土俵にすら立てない

という怖さを持った問題セットです。

検定はついつい「平均の差の検定」など個別の検定手法を優先し、検出力／一様最強検出力検定は後手になりがちで試験会場で思わず天を仰いだ人もいたと思います。逆に言うと検定の評価方法である

• 仮説検定の過誤と検出力関数
• 一様最強検出力検定とネイマン・ピアソンの補題
• 単調尤度比とKarlin-Rubinの定理

をきっちり準備してきた人には易しい問題だと思います。

問題

（出典：「統計検定 1級・準1級 公式問題集」。問題文を一部略記。）

問1

帰無仮説[math]H_0[/math]が正しいとすると[math]\bar{X}\sim N(0, \frac{1}{n})[/math]なので[math]\bar{X}=\bar{x}[/math]が観測された時のP値は[math]W\sim N(0, \frac{1}{n}), Z\sim N(0,\ 1)[/math]および標準正規分布の累積分布関数[math]\Phi(x)[/math]を用いて

[math]
\begin{eqnarray}
&&P(W\geq \bar{x}) \\
&=& P(Z \geq \sqrt{n}\bar{x}) \\
&=& 1 – \Phi(\sqrt{n}\bar{x})
\end{eqnarray}
[/math]

となるので

• [math]\bar{x}=0.3[/math]の時、P値[math]=1-\Phi(\sqrt{10}\times 0.3)=0.17[/math]
• [math]\bar{x}=0.6[/math]の時、P値[math]=1-\Phi(\sqrt{10}\times 0.6)=0.03[/math]

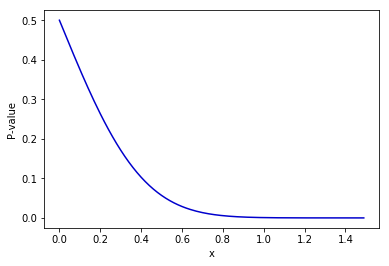
である。またP値[math]=1 – \Phi(\sqrt{n}\bar{x}))[/math]のグラフは下図になる。

問2

問1よりP値[math]=1 – \Phi(\sqrt{n}\bar{x}))[/math]である。また、

[math]
\begin{eqnarray}
&&1 – \Phi(\sqrt{n}\bar{x})) < \alpha \\ &\Leftrightarrow& \sqrt{n}\bar{x} > z_\alpha \\
&\Leftrightarrow& \bar{x} > \dfrac{z_\alpha}{\sqrt{n}} \\
&\Leftrightarrow& \bar{x} \in R
\end{eqnarray}
[/math]

である。

問3

[math]\bar{X}\sim N(\mu, \frac{1}{n})[/math]の時の検出力[math]\beta(\mu)[/math]は

[math]
\begin{eqnarray}
\beta(\mu) &=& P(\bar{X}\in R) \\
&=& P\left(\frac{\bar{X}-\mu}{1/\sqrt{n}} > z_\alpha-\sqrt{n}\mu\right) \\
&=& 1-\Phi\left(z_\alpha-\sqrt{n}\mu\right)
\end{eqnarray}
[/math]

となる。これと[math]z_{0.05}=1.64[/math]であることから

• [math]n=9[/math]の時

  [math]
  \begin{eqnarray}
  \beta(0.4) &=& 0.33 \\
  \beta(0.8) &=& 0.78
  \end{eqnarray}
  [/math]

• [math]n=16[/math]の時

  [math]
  \begin{eqnarray}
  \beta(0.4) &=& 0.48 \\
  \beta(0.8) &=& 0.94
  \end{eqnarray}
  [/math]

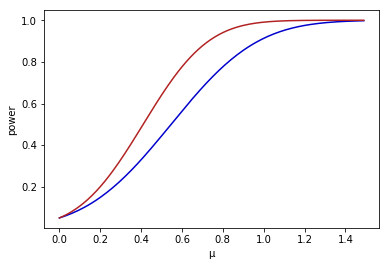
になる。検出力関数を図示すると以下になる。（青線が[math]n=9[/math], 赤線が[math]n=16[/math]の場合の検出力を示す。）

問4

[math]
\begin{eqnarray}
&& \beta(0.5)\geq 0.8 \\
&\Leftrightarrow& \Phi\left(z_{0.05}-0.5\sqrt{n}\right) \leq 0.2 \\
&\Leftrightarrow& z_{0.05}-0.5\sqrt{n} \leq z_{0.8} \\
&\Leftrightarrow& n \geq 4(z_{0.05}-z_{0.8})^2
\end{eqnarray}
[/math]

となり[math]z_{0.05}=1.64, z_{0.8}=-z_{0.2}=-0.84[/math]より

[math]
n\geq 24.6
[/math]

なので[math]n \geq 25[/math]である。

問5

まず[math]\mu=\mu_1(>0)[/math]を固定し単純仮説

• [math]{H’}_0:\ \mu = 0[/math]
• [math]{H’}_1:\ \mu = \mu_1 > 0[/math]

を考える。ネイマン・ピアソンの補題より定数[math]k > 0[/math]と尤度比[math]\lambda(\mathbf{x})=\dfrac{f(\mathbf{x}|0)}{f(\mathbf{x}|\mu_1)}[/math]を用いて

• [math]\lambda(\mathbf{x}) < k[/math]ならば[math]{H'}_0[/math]を棄却
• [math]\lambda(\mathbf{x}) \geq k[/math]ならば[math]{H’}_0[/math]を採択

とした検定は一様最強検出力検定である。

ここで

[math]
\begin{eqnarray}
&& \lambda(\mathbf{x}) \\
&=&\dfrac{f(\mathbf{x}|0)}{f(\mathbf{x}|\mu_1)} \\
&=& \exp\left[-\dfrac{1}{2}\sum_{i=1}^nx_i^2 + \dfrac{1}{2}\sum_{i=1}^n(x_i-\mu_1)^2 \right] \\
&=& \exp\left[n\mu_1\left(\dfrac{1}{2}\mu_1-\bar{x}\right)\right]
\end{eqnarray}
[/math]

と[math]\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i[/math]の単調減少関数になるので定数[math]c[/math]が存在し

[math]
\begin{eqnarray}
&&\lambda(\mathbf{x}) < k \\ &\Leftrightarrow& \bar{x} > c
\end{eqnarray}
[/math]

となるので棄却域[math]R[/math]は[math]\{\bar{x}\ |\ \bar{x} > c\}[/math]と書ける。ここで[math]c=\dfrac{z_\alpha}{\sqrt{n}}[/math]とおくと帰無仮説[math]{H’}_0[/math]の下で

[math]
P\left(\bar{X} > \dfrac{z_\alpha}{\sqrt{n}}\right) = \alpha
[/math]

となるので単純仮説（帰無仮説[math]{H’}_0[/math], 対立仮説[math]{H’}_1[/math]）に対する有意水準[math]\alpha[/math]の一様最強検出力検定である。さらに[math]\mu_1>0[/math]は任意なので片側検定（帰無仮説[math]H_0[/math], 対立仮説[math]H_1[/math]）に対する一様最強検出力検定である。

シリーズ記事

• 過去問と解答例
• 2015年（統計数理）大問1
• 2015年（統計数理）大問1 解答例
• 2015年（統計数理）大問2
• 2015年（統計数理）大問2 解答例（本記事）
• 2015年（統計数理）大問3
• 2015年（統計数理）大問3 解答例