正規母集団の等分散性に関する検定の導出

汎用的な検定方法として尤度比

[math]
\lambda(\mathbf{x}) = \dfrac{\sup_{\theta\in\Theta_0}L(\theta\ |\ \mathbf{x})}{\sup_{\theta\in\Theta}L(\theta\ |\ \mathbf{x})}
[/math]

を使った「尤度比検定」を紹介しました。

ここでは

2つの母集団がそれぞれ正規分布[math]\mathcal{N}(\mu_1, \sigma_1^2)[/math], [math]\mathcal{N}(\mu_2, \sigma_2^2)[/math]に従う

の場合に等分散性（[math]\sigma_1^2=\sigma_2^2[/math]か否か）に関する尤度比検定は「[math]F[/math]分布を使った検定」に帰着できることを示します。帰着するまでの計算が煩雑なので類似の計算が出てくる「正規母集団（分散未知）の平均に関する検定の導出」を事前に参照頂くことをオススメします。

問題設定

2つの母集団から無作為抽出した標本[math]X_i(i=1,\dots,m)[/math]と[math]Y_j(j=1,\dots,n)[/math]はそれぞれ正規分布[math]\mathcal{N}(\mu_1, \sigma_1^2)[/math], [math]\mathcal{N}(\mu_2, \sigma_2^2)[/math]に従うとします^[1]以降の計算が煩雑だと感じる方はまずは[math]m=n[/math]の場合を考えてみると道筋が見えやすくなると思います。。これらの標本に基づいて分散[math]\sigma_1^2, \sigma_2^2[/math]に関する次の両側検定を考えます。

• [math]H_0[/math]: [math]\sigma_1^2 = \sigma_2^2[/math]
• [math]H_1[/math]: [math]\sigma_1^2 \ne \sigma_2^2[/math]

なお、帰無仮説が棄却された場合には分散が異なる（分散が等しいとは考えにくい）と言えますが、帰無仮説が採択された場合には

分散が等しいことを否定する材料は見つからなかった

というだけで等分散性を示しているわけではない（別の検定量を使うことで等分散性が否定される可能性がある）ことには注意しましょう。

尤度比検定

まず、正規分布[math]\mathcal{N}(\mu, \sigma^2)[/math]の確率密度関数[math]f(x|\mu,\sigma)[/math]は

[math]
f(x|\mu,\sigma)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(x-\mu)^2}{2\sigma^2} \right]
[/math]

になります。なお、計算と表記をシンプルにするため平均[math]\mu[/math]と標準偏差[math]\sigma[/math]をパラメータとします。

尤度関数[math]L(\mu_1,\sigma_1, \mu_2, \sigma_2|\mathbf{x})[/math]は[math]C=\frac{1}{\sqrt{2\pi}}[/math]とおくと

[math]
\begin{eqnarray}
&& L(\mu_1,\sigma_1, \mu_2, \sigma_2|\mathbf{x})\\
&=& \prod_{i=1}^{m} f(x_i|\mu_1,\sigma_1)\times \prod_{j=1}^{n} f(y_j|\mu_2,\sigma_2)\\
&=& \dfrac{C^m}{\sigma_1^m} \exp\left[-\frac{1}{2\sigma_1^2}\sum_{i=1}^m (x_i-\mu_1)^2 \right] \\
&&\ \times \dfrac{C^n}{\sigma_2^n} \exp\left[-\frac{1}{2\sigma_2^2}\sum_{j=1}^n (y_j-\mu_2)^2 \right]
\end{eqnarray}
[/math]

となります。

パラメータ空間[math]\Theta[/math]は

[math]
\Theta = \left\{ (\mu_1,\sigma_1, \mu_2, \sigma_2)\in\mathbb{R}^4 \ |\ \sigma_1 > 0,\ \sigma_2 > 0 \right\}
[/math]

になり、帰無仮説のパラメータ空間は

[math]
\Theta_0 = \left\{ (\mu_1,\sigma_1, \mu_2, \sigma_2)\in\mathbb{R}^4 \ |\ \sigma_1=\sigma_2 > 0 \right\}
[/math]

になります。

尤度比[math]\lambda(\mathbf{x})[/math]は定義より

[math]
\lambda(\mathbf{x}) = \dfrac{\sup_{\Theta_0}L(\mu_1,\sigma_1, \mu_2, \sigma_2|\mathbf{x})}{\sup_{\Theta}L(\mu_1,\sigma_1, \mu_2, \sigma_2|\mathbf{x})}
[/math]

なので分子／分母の値を求めるために対数尤度を計算すると

[math]
\begin{eqnarray}
&& \log L(\mu_1,\sigma_1, \mu_2, \sigma_2\ |\ \mathbf{x}) \\
&=& m(\log C – \log \sigma_1)-\frac{1}{2\sigma_1^2}\sum_{i=1}^m (x_i-\mu_1)^2 \\
&&+n(\log C – \log \sigma_2)-\frac{1}{2\sigma_2^2}\sum_{j=1}^n (y_j-\mu_2)^2
\end{eqnarray}
[/math]

になります。まず、分母の尤度を求めるために

[math]
\begin{cases}
\dfrac{\partial (\log L)}{\partial \mu_i} = 0 \quad (i=1,2)\\
\dfrac{\partial (\log L)}{\partial \sigma_i} = 0 \quad (i=1,2)
\end{cases}
[/math]

を解くと

[math]
\begin{cases}
\mu_1 = \dfrac{1}{m}\sum_{i=1}^m x_i \\
\mu_2 = \dfrac{1}{n}\sum_{j=1}^n y_j \\
\sigma_1^2 = \dfrac{1}{m}\sum_{i=1}^m (x_i – \mu_1)^2 \\
\sigma_2^2 = \dfrac{1}{n}\sum_{j=1}^n (y_j – \mu_2)^2
\end{cases}
[/math]

を得ます。つまり分母の尤度は

• [math]\mu_1[/math]が標本平均[math]\bar{x}=\frac{1}{m}\sum_{i=1}^m x_i[/math]
• [math]\sigma_1^2[/math]が標本分散[math]s_1^2=\frac{1}{m}\sum_{i=1}^m (x_i – \bar{x})^2[/math]
• [math]\mu_2[/math]が標本平均[math]\bar{y}=\frac{1}{n}\sum_{j=1}^n y_j[/math]
• [math]\sigma_2^2[/math]が標本分散[math]s_2^2=\frac{1}{n}\sum_{j=1}^n (y_j – \bar{y})^2[/math]

に等しい時に最大値

[math]
\begin{eqnarray}
&& L(\bar{x}, s_1, \bar{y}, s_2) \\
&=& \dfrac{C^m}{s_1^m} \exp\left[-\frac{1}{2s_1^2}\sum_{i=1}^m (x_i-\bar{x})^2 \right] \\
&&\ \times \dfrac{C^n}{s_2^n} \exp\left[-\frac{1}{2s_2^2}\sum_{j=1}^n (y_j-\bar{y})^2 \right] \\
&=& \dfrac{C^{m+n}}{s_1^m s_2^n} \exp\left[-\frac{m+n}{2} \right]
\end{eqnarray}
[/math]

を取ることがわかります。

次に分子を求めると[math]\sigma=\sigma_1=\sigma_2>0[/math]とおいて

[math]
\begin{cases}
\dfrac{\partial (\log L)}{\partial \mu_i} = 0 \quad (i=1,2)\\
\dfrac{\partial (\log L)}{\partial \sigma} = 0
\end{cases}
[/math]

を解くと

[math]
\begin{cases}
\mu_1 = \dfrac{1}{m}\sum_{i=1}^m x_i \\
\mu_2 = \dfrac{1}{n}\sum_{j=1}^n y_j \\
\sigma^2 = \dfrac{ms_1^2+ns_2^2}{m+n}
\end{cases}
[/math]

を得ます。ここで[math]s^2=\frac{ms_1^2+ns_2^2}{m+n}[/math]と置くと分子の最大尤度は

[math]
\begin{eqnarray}
&& L(\bar{x}, s, \bar{y}, s) \\
&=& \dfrac{C^m}{s^m} \exp\left[-\frac{1}{2s^2}\sum_{i=1}^m (x_i-\bar{x})^2 \right] \\
&&\ \times \dfrac{C^n}{s^n} \exp\left[-\frac{1}{2s^2}\sum_{j=1}^n (y_j-\bar{y})^2 \right] \\
&=& \dfrac{C^{m+n}}{s^{m+n}} \exp\left[-\frac{m+n}{2} \right]
\end{eqnarray}
[/math]

になります。

これより尤度比は

[math]
\begin{eqnarray}
&& \lambda(\mathbf{x}) \\
&=& \left(\dfrac{s_1^2}{s^2}\right)^{m/2}\left(\dfrac{s_2^2}{s^2}\right)^{n/2}
\end{eqnarray}
[/math]

になります。ここで、[math]f=\frac{ns_2^2}{ms_1^2} > 0[/math]とおくと

[math]
\begin{eqnarray}
\dfrac{s^2}{s_1^2} &=& \left(\dfrac{m+ns_2^2/s_1^2}{m+n}\right)^{m/2} \\
&=& \left(\dfrac{m}{m+n}(1+ns_2^2/{ms_1^2})\right)^{m/2} \\
&=& \left(\dfrac{m}{m+n}(1+f)\right)^{m/2} \\
\end{eqnarray}
[/math]

と書け、同様に

[math]
\dfrac{s^2}{s_2^2} = \left(\dfrac{n}{m+n}(1+1/f)\right)^{n/2} \\
[/math]

と書けることに注意すると尤度比の逆数[math]1/\lambda(\mathbf{x})[/math]は適当な定数[math]D > 0[/math]を用いて

[math]
1/\lambda(\mathbf{x})=D(1+f)^{m/2}(1+1/f)^{n/2}
[/math]

と書けます。これを[math]f( > 0)[/math]の関数とみて増減を調べるとある定数[math]c > 0[/math]が存在して尤度比の逆数は

• [math]f < c[/math]で単調減少
• [math]f \geq c[/math]で単調増加

となることが分かります。したがって、尤度比は

• [math]f < c[/math]で単調増加
• [math]f \geq c[/math]で単調減少

になるため任意の定数[math]k[/math]に対して定数[math]a > 0, b > 0[/math]が存在して

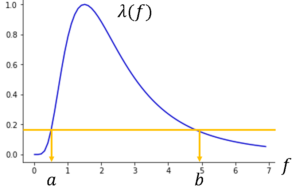
[math]
\lambda(\mathbf{x}) \leq k \Leftrightarrow f \leq a\ {\rm or} \ f \geq b
[/math]

が成立するので尤度比検定は次の形に書くことができます。

正規母集団の等分散性に関する検定

1. 事前に有意水準[math]\alpha[/math]を決め棄却域[math]R=\left\{f\ |\ f \leq a_\alpha \ {\rm or} \ f \geq b_\alpha \right\}[/math] を設定する。
2. 統計量[math]F=\dfrac{ns_2^2}{ms_1^2}[/math]を計算する。
3. [math]F \in R[/math]ならば帰無仮説を棄却し、そうでないなら帰無仮説を採択する。

帰無仮説の下では[math]\dfrac{ns_2^2}{\sigma^2}[/math]と[math]\dfrac{ms_1^2}{\sigma^2}[/math]は互いに独立でそれぞれ自由度[math]n-1[/math]および[math]m-1[/math]の[math]\chi^2[/math]分布に従うことから統計量[math]F=\dfrac{ns_2^2}{ms_1^2}[/math]は自由度[math](n-1,m-1)[/math]の[math]F[/math]分布に従います。したがって、両側検定の場合は棄却域[math]R[/math]を[math]F[/math]分布の上側[math]p\%[/math]点[math]F_{n-1,m-1}(p)[/math]を用いて

[math]
\begin{eqnarray}
R&=&\left\{f\ |\ f \leq F_{n-1, m-1}(1-\alpha/2) \ {\rm or} \right.\\
&&\quad \quad \left. f \geq F_{n-1, m-1}(\alpha/2) \right\}
\end{eqnarray}
[/math]

と書けます。

シリーズ記事

• 正規母集団（分散既知）の平均に関する検定の導出
• 正規母集団（分散未知）の平均に関する検定の導出
• 正規母集団の等分散性に関する検定の導出（本記事）