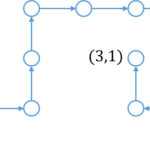
調査から得たデータは4つの尺度水準
- 名義尺度
- 順序尺度
- 間隔尺度
- 比例尺度
に分けられます。
データに対して可能な演算(ex. 足し算、掛け算や平均を取るなど)は尺度水準に依存し、要約統計量や検定法は尺度水準に応じて適切に選定する必要があります。統計の教科書では最初の方に出てくるため忘れやすく、間違った要約統計量を使ってしまうことも多いので、ここでは改めてその定義と適用可能な演算、統計量についてまとめます。
名義尺度
名義尺度では測定対象の違いを識別するために数字を割り振ります。たとえば血液型を測定した際に4つの血液型(A型、B型、AB型、O型)を識別するために順に1~4の数値を割り当てるケースが該当します。
この水準では値の比較は「等しいか」「異なるか」でしか行えないため
- 順序比較はできない
- 加減算はできない
- 乗除算はできない
です。したがって、件数のカウントぐらいしかできることはなく要約統計量としては最頻値のみ使えます。
順序尺度
順序尺度では対象の性質の順序を現す数値を割り振ります。たとえば震度は地震の揺れの大きさに応じて「震度0」~「震度7」まで設定しており順序尺度になります。
この水準では値の大小比較は行えますが、加減乗除の演算には意味がなく
- 順序比較はできる
- 加減算はできない
- 乗除算はできない
になります。たとえば「震度3」は「震度1」より大きいことを意味しますが、「震度1が3回あると震度3」「震度3は震度1より3倍大きい」という意味にはなりません。
要約統計量としては最頻値に加え中央値が使えますし、順位相関係数を算出してデータ間の相関を分析することもできます。
間隔尺度
間隔尺度では順序尺度の性質を満たし、さらに「差が等しい」ことが「間隔が等しい」ことを意味するように数値を割り振ります。たとえば温度(摂氏や華氏)、日付は間隔尺度になります。
この水準では加減算ができ、測定対の差の比較もできますが乗除の演算には意味がなく
- 順序比較ができ、測定対の差の比較も可能
- 加減算ができる
- 乗除算はできない
になります。たとえば「1月1日」を1として以降連番で日付に数値を振った場合、「1月1日」(=1)の3日後(+3)は「1月4日」(=4)と意味がありますが、「1月3日」(=3)の3倍は「1月9日」と意味のない結果になります。
要約統計量としては最頻値、中央値に加え算術平均が使え、分散や相関係数など多くの統計量が計算可能です。次の比例尺度と比べても差は少なく間隔尺度と比例尺度の区別が必要となる場面は少ないと思います。実際、間隔尺度と比例尺度を合わせて「計量尺度」と呼ぶこともあります。
比例尺度
比例尺度では間隔尺度の性質を満たし、さらにペアの比にも乗除の演算にも意味があるように数値を割り振ります。質量、長さなどの物理量や年齢、収入などは比例尺度になります。
この水準では加減乗除算ができ、測定対の差/比の比較もでき
- 順序比較ができ、測定対の差/比の比較も可能
- 加減算ができる
- 乗除算もできる
になります。
要約統計量としては最頻値、中央値、算術平均に加え幾何平均が使えます。
参考情報
- Wikipedia「尺度水準」
- 入門 統計学(栗原 伸一 著)
: 「1.1 記述統計学と測定尺度」に例とともに丁寧な解説があります。