引き続き特徴量と生存率の関係を見ていきます。前半編でも触れたように
- 特徴量の変化によって生存率に差がでるか?
- 特徴量の変化に対して生存率が上下したり非単調な変化をしていないか?
を確認します。なお、Jupyter notebookのコードも公開しているので、実行しながら読むとより理解しやすいと思います。
一緒に乗船した兄弟、配偶者の数(SibSp)

SibSpは4以上のサンプル数が少ないので4に丸めています。
- 0から1に増えると生存率は34.5%から53.6%に増える
- 1以降は単調に減少する
と非単調な変化をしています。SibSpの線形モデルではうまく表現できないですが
生存率 = a x (SibSp) + b x (SibSp=0フラグ) + c
で概ね表現できそうなので「SibSp=0フラグ」を入れるのが良さそうです。
一緒に乗船した親子の数(Parch)

Parchは3以上のサンプル数が少ないので3に丸めています。
- 0から1に増えると生存率は34.4%から55.1%に増える
- 1以降は単調に減少する
と非単調な変化をしており「Parch=0フラグ」を入れるのが良さそうです。
運賃(Fare)
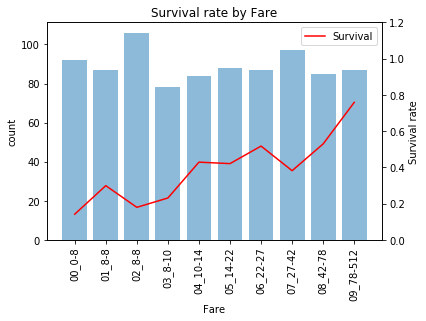
運賃が上がるにつれ、生存率も上がる傾向がありますね。分布の裾が長いので外れ値を考慮する必要はありますがそのまま使っても良さそうです。
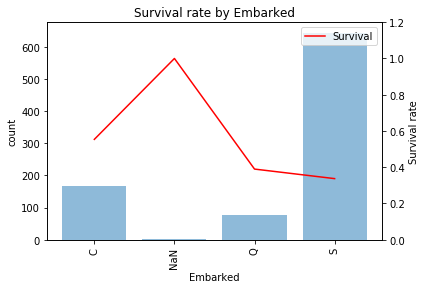
乗船港(Embarked)
C(55.4%) > Q(39.0%) > S(33.7%)
Cの生存率が高いです。地域ごとに所得水準に違いがありチケットクラスに違いがあるのかもしれません。
乗船港別のチケットクラス
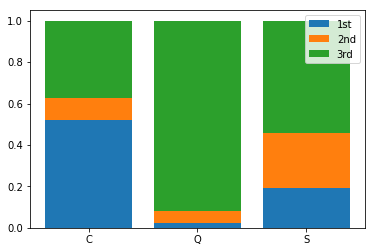
乗船港ごとにチケットクラスの割合を集計したのが上図です。これを見ると
- Cの半数以上(52.2%)が1stに乗船
- Qの大半(91.9%)が3rdに乗船
と乗船港によりチケットクラスの割合が大きく違います。むしろQは3rdが大半の割には生存率が高く、同じチケットクラスでも乗船港で生存率に差があることを示しています。一つ可能性があるのが
1912年4月10日に、タイタニックはエドワード・J・スミス船長の指揮のもと、イギリス・サウサンプトン港の専用埠頭オーシャンドックからニューヨーク行きの処女航海に出発した。(中略)予定通りフランスのシェルブールとアイルランドのクイーンズタウン(現コーヴ) に寄港し、アメリカのニューヨークに向かった。
(出典:Wikipedia「タイタニック(客船)」)
とS、C、Qの順に寄港しており同じクラスでも乗船時間を短くするため出発港(=S)は奥の客室を、寄港地(=C, Q)は入口に近い客室を割り当てたのかもしれません。客室番号(Cabin)の多くが欠損しており正確なところはわかりませんが、乗船港が情報を持っていることは確かなのでダミー変数化して使うのが良いでしょう。
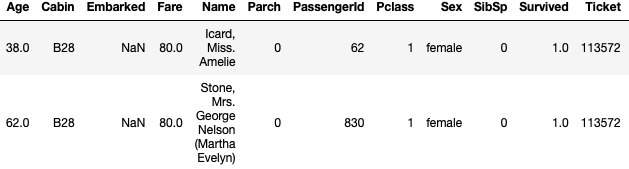
欠損値
乗客2人の乗船港が欠損になっています。補完の仕方は色々考えられますが2人とも1stクラスの乗客なのでチケットクラス(1st)の下で乗船港の条件付き確率を求めると
[math]P({\rm Q | 1st}) < P({\rm C | 1st}) < P({\rm S | 1st})[/math]
なので「S」で補完することにします。
クロス集計(後半)のまとめ
クロス集計の結果をまとめます。
- 一緒に乗船した兄弟、配偶者の数: 1以上では単調に減少。「SibSp」と「SibSp=0フラグ」を使う
- 一緒に乗船した親子の数: 1以上では単調に減少。「Parch」と「Parch=0フラグ」を使う
- 運賃: 概ね単調に増加。そのまま使っても良さそう
- 乗船港: 生存率に差がある。チケットクラスの偏りを考慮しても差がありダミー変数化して使うのが良さそう。欠損値は「S」で補完
一通り使いやすそうなデータの可視化/理解ができたのでいよいよモデル構築、予測結果のSubmitをやっていきましょう。