階乗[math]n![/math]をより扱いやすい指数形式で近似する「スターリングの公式」(Stirling’s formula)は理論上も応用上も非常に重要な公式です。
近似精度に応じたいくつかの式がありここでは一番シンプルな階乗の対数を近似する
[math]
\log n! \sim n\log n – n
[/math]
を紹介します。対数を戻すと[math]n![/math]はおおよそ[math]\left(\frac{n}{e}\right)^n[/math]になることがわかります。
漸近近似の定義
まず記号の定義をします。ある関数[math]f(n), g(n)[/math]の比が[math]n\to\infty[/math]で1に収束するとき、つまり
[math]
\displaystyle \lim_{n\to\infty} \dfrac{f(n)}{g(n)} = 1
[/math]
の時
[math]
f(n) \sim g(n)
[/math]
と定義します。この時、[math]g(n)[/math]は[math]f(n)[/math]に漸近近似するといいます。
[math]\log n![/math]の不等式評価
まず[math]\log n!=\sum_{k=1}^n \log k[/math]を上から評価します。
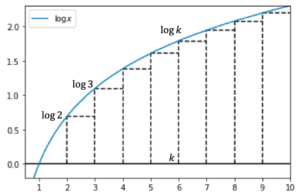
上図より区間[math][k, k+1][/math]の四角形の面積は[math]\log k[/math]で[math]\int_k^{k+1} \log x dx[/math]より小さいので[math]k=1,2,\dots, n-1[/math]について足し合わせて
[math]
\begin{eqnarray}
\sum_{k=1}^{n-1}\log k &<& \int_1^{n} \log x dx \\
&=& \left[x\log x - x\right]_1^n \\
&=& n \log n - n + 1
\end{eqnarray}
[/math]
がわかります。両辺に[math]\log n[/math]を足して
[math]
\log n! < (n+1)\log n - n + 1
[/math]
が得られます。
次に下からの評価を求めます。
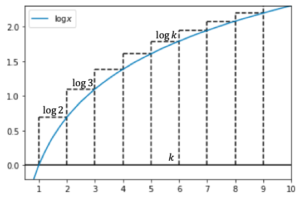
上図より区間[math][k-1, k][/math]の四角形の面積は[math]\log k[/math]で[math]\int_{k-1}^{k} \log x dx[/math]より大きいので[math]k=2,\dots, n[/math]について足し合わせて
[math]
\begin{eqnarray}
\sum_{k=2}^{n}\log k &>& \int_1^{n} \log x dx \\
&=& \left[x\log x – x\right]_1^n \\
&=& n \log n – n + 1
\end{eqnarray}
[/math]
がわかります。両辺に[math]\log 1(=0)[/math]を足して上からの評価とまとめると
[math]
\begin{eqnarray}
&& n\log n – n + 1 < \log n! \\
&& \quad < (n+1)\log n - n + 1
\end{eqnarray}
[/math]
が得られます。
[math]\log n![/math]の漸近近似
[math]\log n![/math]の不等式評価から
[math]
\begin{eqnarray}
&& 1 + \dfrac{1}{n\log n – n} < \dfrac{\log n!}{n\log n - n} \\
&& \quad < 1 + \dfrac{\log n + 1}{n\log n - n}
\end{eqnarray}
[/math]
なので[math]n\to\infty[/math]で[math]\dfrac{\log n!}{n\log n – n}[/math]は1に収束します。つまり
[math]
\log n! \sim n\log n – n
[/math]
であり[math]n\log n – n[/math]は[math]\log n![/math]の漸近近似になっています。
[math]n\log n-n[/math]の近似精度
ここでは[math]n\log n – n[/math]の近似精度を見てみます。[math]y=\log nと[math]y=n\log n – n[/math](オレンジ線)をplotすると下図になり良い近似になっているのがわかります。

具体的に[math]n=5, 10, 20, 50, 100, 1000[/math]の値を計算してみると
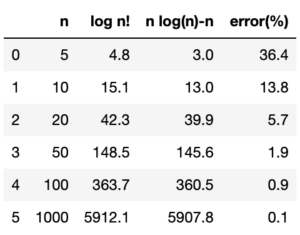
と[math]n[/math]が大きくなるにつれ誤差も小さくなることがわかります。
[math]n![/math]と[math]\left(\frac{n}{e}\right)^n[/math]の比較
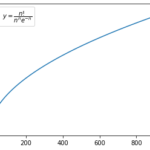
[math]\log n!\sim n\log n – n[/math]が得られたので対数を戻して[math]n![/math]と[math]\left(\frac{n}{e}\right)^n[/math]を比較してみます。
同じように[math]n=5, 10, 20, 50, 100[/math]の値を計算してみると
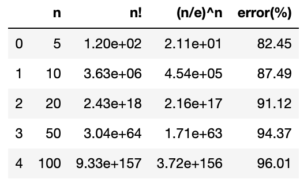
- [math]n=20[/math]で[math]20!=2.43\times 10^{18}[/math], [math]\left(\frac{20}{e}\right)^{20}=2.16\times 10^{17}[/math]と一桁の違いがある
- [math]n[/math]が大きくなるにつれ誤差も大きくなる
とどうやら[math]\left(\frac{n}{e}\right)^n[/math]は[math]n![/math]の漸近近似にはなっていないようです。
実は[math]n![/math]の漸近近似を与えるスターリングの公式
[math]
n! \sim \sqrt{2\pi n}\left(\dfrac{n}{e}\right)^n
[/math]
が知られており次の記事ではその導出を行います。



下からの評価の不等号が逆だと感じました。