前回の記事「スターリングの公式(対数近似編)」では階乗の対数[math]\log n![/math]の漸近近似
[math]
\log n! \sim n \log n – n
[/math]
を求めました。ただ、対数を戻した[math]n![/math]と[math]\left(\frac{n}{e}\right)^n[/math]の比較では誤差がどんどん大きくなっていくこともわかりました。ここではスターリングの公式として知られる漸近近似
[math]
n! \sim \sqrt{2\pi n}\left(\dfrac{n}{e}\right)^n
[/math]
を導出します。ここではスターリングの公式が解決されるまでの歴史に沿う形で
- [math]\frac{n!}{n^ne^{-n}}[/math]の挙動から漸近近似式を予想
- 数列[math]a_n=\frac{n!}{\sqrt{n}n^ne^{-n}}[/math]の収束を証明
- 数列[math]a_n[/math]の極限の算出
の順で説明していきます。また、数列[math]a_n[/math]の性質から不等式評価
[math]
\sqrt{2\pi n}\left(\dfrac{n}{e}\right)^n \leq n! \leq e\sqrt{n}\left(\dfrac{n}{e}\right)^n
[/math]
も求めることができます。途中、やや難しいところもありますが初等的(高校数学の範囲)に示すことができます。
なお、以下の2つの記事の結果を用いるので合わせて参照ください。
[math]\frac{n!}{n^ne^{-n}}[/math]の挙動
まず[math]n![/math]とその対数近似[math]\left(\frac{n}{e}\right)^n[/math]のずれを見るために比[math]\frac{n!}{n^ne^{-n}}[/math]をplotしたのが下図です。
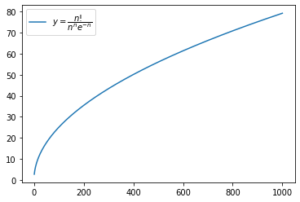
[math]n=200, 600, 1000[/math]で約[math]35, 60, 80[/math]と[math]n[/math]の増加につれ比も緩やかに大きくなります。
ここで両対数グラフを描くと
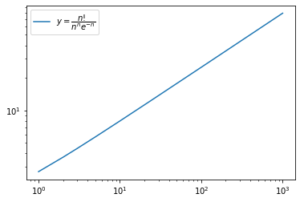
とほぼ直線になることがわかります。
サンプル[math](\log n, \log \frac{n!}{n^ne^{-n}}),\ (n=1,\dots,1000)[/math]から直線を推定すると
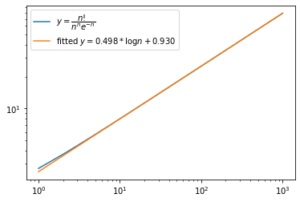
推定式[math]y = 0.498 \log n + 0.930[/math]が得られます。これより
[math]
\begin{eqnarray}
&&\log \dfrac{n!}{n^ne^{-n}} \fallingdotseq 0.498 \log n + 0.930 \\
&\Leftrightarrow&
\dfrac{n!}{n^ne^{-n}} \fallingdotseq e^{0.930} n^{0.498}
\end{eqnarray}
[/math]
となるので[math]\frac{n!}{n^ne^{-n}}[/math]の漸近近似式としてある定数[math]C > 0[/math]が存在して
[math]
\dfrac{n!}{n^ne^{-n}} \sim C\sqrt{n}
[/math]
となるのではと「予想」できます。
数列[math]a_n=\frac{n!}{\sqrt{n}n^ne^{-n}}[/math]の収束を証明
「予想」が正しいことを示すには数列
[math]
a_n = \dfrac{n!}{\sqrt{n}n^ne^{-n}}
[/math]
がある定数[math]C[/math]に収束することを示せばよいです。ここでは
を示します。まず定義より[math]a_n > 0[/math]は自明です。
次に[math]b_{n}=\frac{a_n}{a_{n+1}}[/math]とおくと[math]b_n[/math]は
[math]
\begin{eqnarray}
b_n &=& \dfrac{a_n}{a_{n+1}} \\
&=& \dfrac{n!}{\sqrt{n}n^ne^{-n}} \cdot \dfrac{\sqrt{n+1}(n+1)^{n+1}e^{-(n+1)}}{(n+1)!} \\
&=& \dfrac{1}{e}\left(\dfrac{n+1}{n}\right)^{n+\frac{1}{2}}
\end{eqnarray}
[/math]
と整理でき対数をとると
[math]
\log b_n = \left(n + \dfrac{1}{2}\right)\log \dfrac{n+1}{n} – 1
[/math]
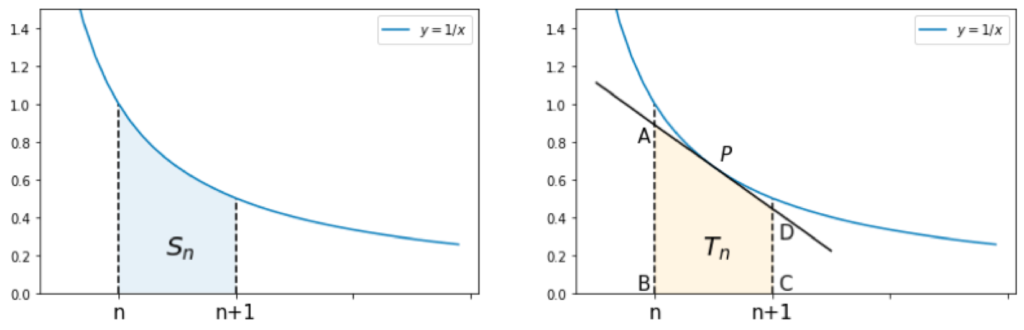
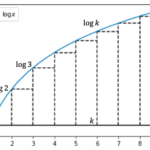
となります。ここで[math]y=\frac{1}{x}[/math]を考えます。
[math]y=\frac{1}{x}[/math]の区間[math][n, n+1][/math]の面積[math]S_n[/math]を考えると[math]S_n=\log (n+1) – \log n[/math]になります。次に点[math]P(n+1/2, \frac{1}{n+1/2})[/math]における接線を考えると台形ABCDの面積[math]T_n[/math]は[math]T_n=\frac{1}{n+1/2}[/math]になります。図より[math]T_n < S_n[/math]なので
[math]
\begin{eqnarray}
&&
\frac{1}{n+1/2} < \log (n+1) - \log n \\
&\Leftrightarrow& 0 < \left(n + \dfrac{1}{2}\right)\log\dfrac{n+1}{n} - 1 \\
&\Leftrightarrow& 0 < \log b_n
\end{eqnarray}
[/math]
が示せます。つまり[math]b_n > 1[/math]なので[math]a_n > a_{n+1}[/math]となり単調減少することがわかります。
単調減少する下に有界な数列は収束するので定数[math]C[/math]が存在して
[math]
\displaystyle
\lim_{n\to\infty}a_n = \lim_{n\to\infty}\dfrac{n!}{\sqrt{n}n^ne^{-n}} = C
[/math]
となります。つまり[math]n![/math]の漸近近似として
[math]
n! \sim C\sqrt{n}\left(\dfrac{n}{e}\right)^n
[/math]
が成立することがわかります。
数列[math]a_n[/math]の極限の算出
ここからは数列[math]a_n[/math]の極限を具体的に求めます。「ウォリスの公式」から二項係数[math]{}_{2n}C_n=\frac{(2n)!}{n!n!}[/math]の漸近近似[math]\frac{4^n}{\sqrt{\pi n}}[/math]がわかっているので[math]{}_{2n}C_n[/math]が現れるように[math]\frac{a_{2n}}{a_n^2}[/math]を考えます。
[math]
\begin{eqnarray}
\dfrac{a_{2n}}{a_n^2} &=& \dfrac{(2n)!}{\sqrt{2n}(2n)^{2n}e^{-2n}}\cdot \dfrac{n^{2n+1}e^{-2n}}{n!n!} \\
&=& \dfrac{1}{4^n}\sqrt{\dfrac{n}{2}}{}_{2n}C_n
\end{eqnarray}
[/math]
となります。これより
[math]
\begin{eqnarray}
\lim_{n\to\infty} \dfrac{a_{2n}}{a_n^2} &=& \lim_{n\to\infty}\dfrac{1}{4^n}\sqrt{\dfrac{n}{2}}\cdot\dfrac{4^n}{\sqrt{\pi n}} \\
&=& \dfrac{1}{\sqrt{2\pi}}
\end{eqnarray}
[/math]
となります。また、[math]n\to\infty[/math]で[math]a_{n}\to C[/math]なので[math]\frac{a_{2n}}{a_n^2}\to\frac{1}{C}[/math]より
[math]
C = \sqrt{2\pi}
[/math]
がわかります。以上よりスターリングの公式
[math]
n! \sim \sqrt{2\pi n}\left(\dfrac{n}{e}\right)^n
[/math]
を求めることができました。
[math]n![/math]の不等式評価
数列[math]a_n[/math]の性質から[math]n![/math]の漸近近似だけではなく上下からの評価を得ることができます。
[math]
\sqrt{2\pi n}\left(\dfrac{n}{e}\right)^n \leq n! \leq e\sqrt{n}\left(\dfrac{n}{e}\right)^n
[/math]
数列[math]a_n[/math]は単調減少かつ[math]C=\sqrt{2\pi}[/math]に収束するので任意の[math]n[/math]で[math]\sqrt{2\pi} \leq a_n \leq a_1[/math], つまり
[math]
\sqrt{2\pi} \leq \dfrac{n!}{\sqrt{n}n^ne^{-n}} \leq a_1=e
[/math]
が成立し、整理すると求める不等式が得られます。
[math]\sqrt{2\pi n}\left(\frac{n}{e}\right)^n[/math]の近似精度
最後にスターリングの公式[math]\sqrt{2\pi n}\left(\frac{n}{e}\right)^n[/math]の近似精度を求めてみましょう。
[math]n=5, 10, 20, 50, 100[/math]の値を計算してみると
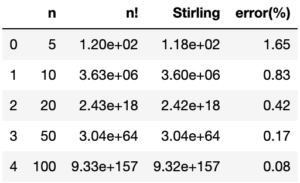
と最初から正確なだけでなく[math]n[/math]が大きくなるにつれどんどん正確になっていくという漸近近似のスゴさがよくわかると思います。


ピンバック: スターリングの公式(対数近似)の導出 | 有意に無意味な話
コメントありがとうございます。修正しました。