2023年8月11日~20日に開催された「RECRUIT 日本橋ハーフマラソン 2023夏(AHC022)」に参加しました。
結果は方針ミスが大きく響いて205位とあまり振るわなかったのですで復習して延長戦順位表で20位付近まで伸びたので主にその振り返りをしたいと思います。
コンテスト/問題概要
[math]N[/math]個の入口と出口がつながった2つの世界([math]L \times L[/math]セルのグリッド)がありどの出口に対応づいているかはわからない。
出口側の各セルに温度[math]T (0 \leq T \leq 1000)[/math]を設定し、入口に対応する出口から適当に移動した場所で温度計測を行う。ただし、温度計測時に平均0, 標準偏差[math]S(1 \leq S \leq 900)[/math]の誤差が生じる。うまく温度設定、移動することで入口と出口の対応関係を求めよ。
スコアは
- 誤判定の個数[math]W[/math]の指数[math]0.8^W[/math]
- 各セル間の温度差の二乗の和の逆数
- 計測時の回数、総移動距離の逆数
に比例する形で与えられており温度差(配置コストと呼ぶ)、計測時の移動距離・回数(計測コスト)を押さえつつ誤判定をなくすのがポイントです。
本番提出解法
本番時は
- 出口付近のセルに高温/低温をセットし識別すれば良さそう
- わざわざ遠くまで計測しに行くメリットはない
と思ったのですが、配置コストを下げるのが難しくスコアが伸び悩んでしまいました。
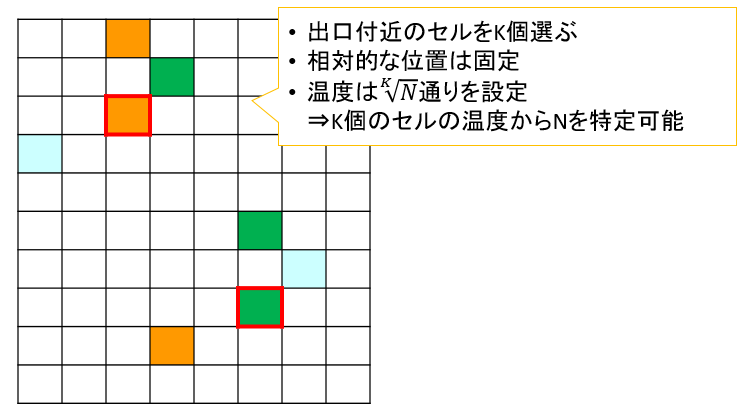
考え方としては平方分割の要領で出口付近のセルを[math]K[/math]個選んで各セルに設定する温度を[math]\sqrt[K]{N}[/math]通りにすると[math]K[/math]個のセルの温度から出口を特定できます。
上図だと赤枠セルが出口を表し水緑橙のセルが温度設定セルで色の違いが設定温度の違いを表します。3通りの温度を4セルで使うと[math]3^4[/math]通りを表現できます。
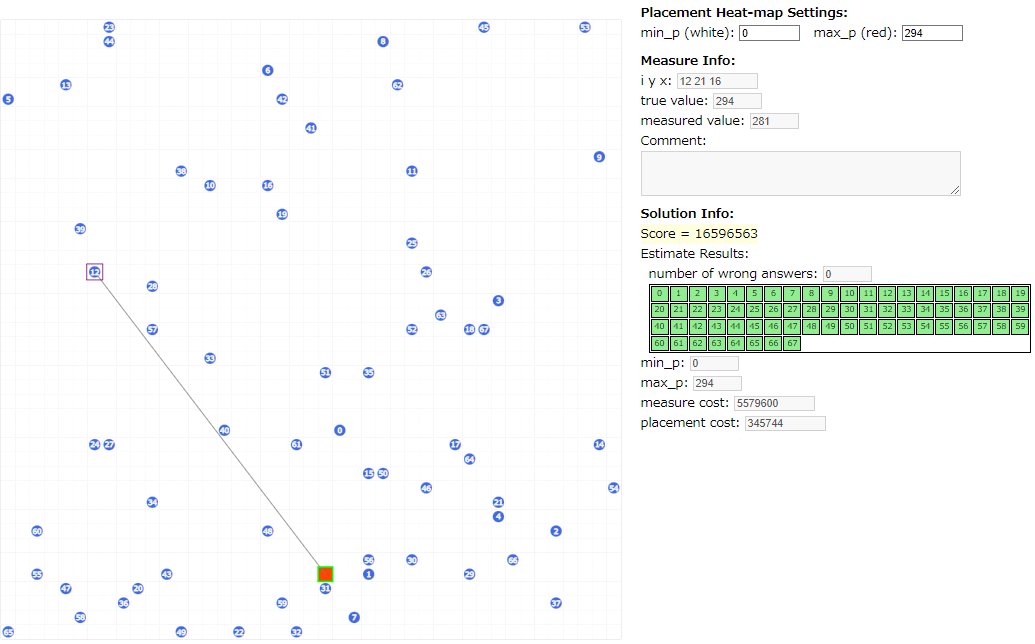
また、許容誤判定率[math]p[/math]と各セルで[math]m[/math]回測定したときの平均温度の標準偏差は[math]S/\sqrt{m}[/math]になり温度幅を決めたときの配置コスト、計測コスト、誤判定する個数の確率分布が出せるのでスコアの期待値を出して一番良いものを選びます。
これで[math]S \leq 600[/math]まではほぼ[math]W=0[/math]にできますが、そこからはWが大きくなります。
そこでハミング符号を使いました。7bit使って4bitの情報を伝えられるので出口ごとに2つ使いました。これだと[math]S=900[/math]でもWを0近くまで落とすことができます。
ただ、その代償に配置コストが[math]10^8[/math]くらいになりトップ層より一桁以上スコアが低い状態で伸び悩むのですが、気づいたのが終了前日の夜で時すでに遅し…でした。
最終日は焼け石に水と思いつつ配置コストが低くなるように焼きなましたりしました。
出力結果を見ながら
「うーん、これはこれで良さそうなんだけど1桁も違う世界があるんだよなぁ」
と思いながらも本質的な改善はできないまま終了。最終的には205位でした。
復習 & 延長戦
Twitterを見ていると出口周囲に情報を埋め込む「QRコード方式」ではなく

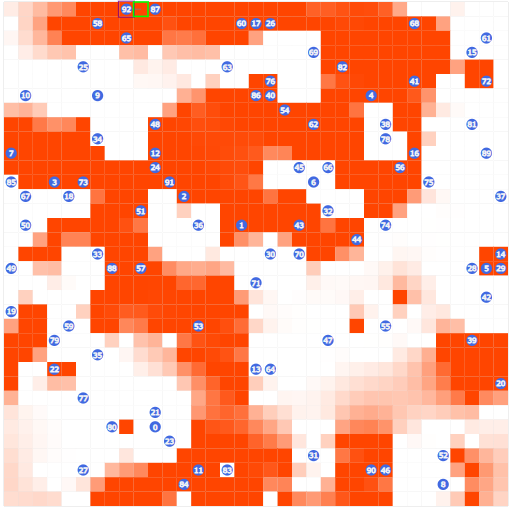
上図のように[math]L/2[/math]の正方形領域だけ高温にしておくと
- どの位置からもx, y方向に0 or [math]L/2[/math]進むと必ず高温域になる
- 高温域の境界との相対位置[math](dy, dx)[/math]が分かれば出口の座標が分かる
- 境界位置は二分探索できる
と目からウロコな解法がありました。
QRコード方式は0, 1000度のセルを全面に配置する必要があり配置コストが高くなりますが、この配置だと0-1000度のセルは[math]L[/math]個なので配置コストは[math]10^8[/math]未満になりますね。
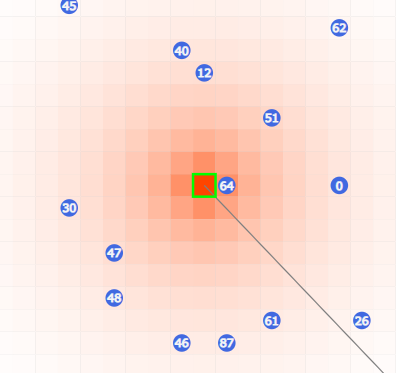
また解説放送で紹介されていた1点高温方式
も面白い解法で
- 1カ所だけ高温域を作る
- 各出口ごとに高温までの相対距離を移動して計測
するとどの出口かを判定できます。また相対距離が近い順に試すこと計測コストを抑えることができます。
これをさらに発展させたのが1点高温+平滑化で
上図のように温度をなめらかにしておきます。単に滑らかにすると高温位置と周辺の温度が近く誤判定が増えるのですが
温度測定ごとにベイズの定理でどの出口に対応するかの確率を更新
しながら対応関係を求めていきます。
こう書くとまぁそういうアイディアもあるよな…という感じですが
- 条件付確率を対数尤度で持つのではなく毎回ベイズの定理で0-1に正規化しておく
- 確率値が閾値を超える or 残りの出口数と計測可能数から対応付けるようにする
- 温度をなめらかにする際も各セルが異なる温度になるようにする
など細かな点も詰めないとうまく推定できなかったり計測回数が増えたりして形にするのが難しかったですね。
大体、このロジックで相対スコア27.0G(本番40位相当)が出ました。
さらにここからの工夫として
- 高温域の周辺だけ温度のばらつきを大きくする
- 高温域を2カ所作る
をしました。
1点目は高温周囲を計測する際に識別しやすくするのが狙いで高温付近だけQRコード方式にするイメージです。Sが大きいところで効果がありました。

上図はseed=33(S=900)で高温付近がモザイク状になっていますね。S=900でもちゃんとすべて正しく推定できるのは驚きです。
2点目は計測コストを減らすのが目的で最寄りの高温域へ行くことで移動距離を減らせます。主にSが小さいところで効果がありました。3か所作るのも試しましたが配置コストの増加に対して計測コストの減少が小さくて採用を見送りました。
これを提出して相対32.6Gで本番20位近くまで伸ばせました。
復習 & 延長戦
終わった後は方針ミスの後悔が大きかったのですが復習して1点高温+平滑化でここまで正しく推定できるのは驚きでした。
さらに高温付近をQRコード方式にすると改善したのでQRコード方式自体が悪いのではなく精度と配置コストのバランスが重要で
情報をリッチに埋め込むのは1-2カ所にして後は「足」と「知恵」で稼ぐ!
のが良かったのですね。
面白い問題で終わってから2週間も楽しめました。リクルートさん、AtCoderさん、そして参加者の皆様ありがとうございました。
さて、これを書いているのは9月3日の朝9時ですがあと1時間もするとAHC023「Asprova プログラミングコンテスト」ですね!こちらも楽しもうと思います。