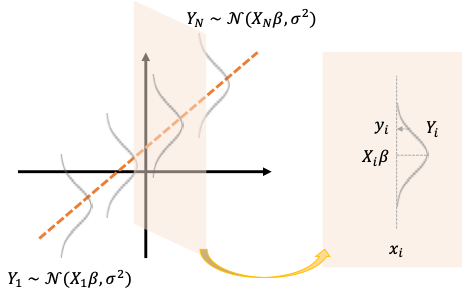
誤差項が独立同一な正規分布に従う場合、「回帰係数の確率分布」の結果から予測区間(Prediction Interval)を構成することができます。
なお、予測区間の意味や解釈の仕方、信頼区間との違いがややこしく誤解しやすいので「単回帰モデルの予測区間」も合わせて参照ください。
確率モデル
表記をシンプルにするためこちらの記事で定義したベクトル、行列を使うと
[math]
\boldsymbol{Y} = \boldsymbol{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon},\ \boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0}, \sigma^2\boldsymbol{I}_N)
[/math]
とかけます。
確率モデルは何が確率変数で何が確定値なのかわかりにくいのでまとめると
- [math]\boldsymbol{X},\ \boldsymbol{y}[/math]: 既知の確定値
- [math]\boldsymbol{\beta},\ \sigma^2[/math]: 未知の確定値
- [math]\boldsymbol{Y},\ \boldsymbol{\varepsilon}[/math]: 確率変数
になります。
最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]と分散の不偏推定量[math]S^2[/math]の確率分布
誤差項が独立同一な正規分布に従う場合、最小二乗推定量[math]\boldsymbol{\hat{\beta}}=\left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T\boldsymbol{Y}[/math]と分散[math]\sigma^2[/math]の不偏推定量[math]S^2=\frac{1}{N-P-1} \left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right)^T\left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right)[/math]の確率分布を求めることができます。
- [math]\boldsymbol{\hat{\beta}}\sim \mathcal{N}\left(\boldsymbol{\beta}, \sigma^2(\boldsymbol{X}^T\boldsymbol{X})^{-1}\right)[/math]
- [math]\frac{(N-P-1)S^2}{\sigma^2} \sim \chi^2_{N-P-1}[/math]
- [math]\boldsymbol{\hat{\beta}}[/math]と[math]S^2[/math]は独立
予測区間と信頼区間の違い
ここからは信頼区間同様に説明変数を[math]\boldsymbol{x}=\boldsymbol{x}_0[/math]と任意に固定して考えます。信頼区間では
誤差項を含まない真の値: [math]\boldsymbol{\beta}^T\boldsymbol{x}_0[/math]
が考察の対象でしたが、予測区間では
誤差項を含む目的変数の値: [math]\boldsymbol{\beta}^T\boldsymbol{x}_0 + \varepsilon[/math]
が考察対象になります。つまり予測区間では「[math]\boldsymbol{x}=\boldsymbol{x}_0[/math]での観測値」がどの区間に入りやすいかを議論します。
目的変数[math]Y[/math]が従う確率分布
[math]x=x_0[/math]での目的変数[math]Y_0[/math]は
[math]
\begin{eqnarray}
Y_0 &=& \boldsymbol{\beta}^T\boldsymbol{x}_0 + \varepsilon \\
&\sim& \mathcal{N}(\boldsymbol{\beta}^T\boldsymbol{x}_0, \sigma^2)
\end{eqnarray}
[/math]
に従います。ただ、[math]\boldsymbol{\beta}, \sigma^2[/math]は未知なので推定量で置き換えることを考えます。
目的変数[math]Y_0[/math]の推定量である[math]\hat{y}_0 = \boldsymbol{\hat{\beta}}^T\boldsymbol{x}_0[/math]との差
[math]
W = Y_0 – \boldsymbol{\hat{\beta}}^T\boldsymbol{x}_0
[/math]
を考えます。[math]Y_0, \hat{y}_0[/math]は正規分布に従うので[math]W[/math]も正規分布に従います。期待値を求めると
[math]
\begin{eqnarray}
E\left[W\right] &=&
E\left[Y_0\right] –
E\left[\boldsymbol{\hat{\beta}}^T\boldsymbol{x}_0\right] \\
&=& \boldsymbol{\beta}^T\boldsymbol{x}_0 – \boldsymbol{\beta}^T\boldsymbol{x}_0 \\
&=& 0
\end{eqnarray}
[/math]
です。[math]\boldsymbol{x}_0[/math]は学習データ[math]\boldsymbol{X}[/math]に依存しないので[math]Y_0[/math]は[math]\boldsymbol{\hat{\beta}}[/math]とは独立になり分散は
[math]
\begin{eqnarray}
V\left[W\right] &=& V\left[Y_0\right] + V\left[\boldsymbol{\hat{\beta}}^T\boldsymbol{x}_0\right] \\
&=& \sigma^2 \left(1 + \boldsymbol{x}_0^T \left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1} \boldsymbol{x}_0\right)
\end{eqnarray}
[/math]
になります。
さらに[math]Y_0, \boldsymbol{\hat{\beta}}[/math]は[math]S^2[/math]と独立なので統計量[math]T[/math]は
[math]
\begin{eqnarray}
T &=& \dfrac{\frac{Y_0 – \boldsymbol{\hat{\beta}}^T\boldsymbol{x}_0}{\sqrt{V\left[W\right]}}}{\sqrt{\frac{(N-P-1)S^2}{\sigma^2}\cdot \frac{1}{N-P-1}}} \\
&=& \dfrac{Y_0 – \boldsymbol{\hat{\beta}}^T\boldsymbol{x}_0}{S\sqrt{1+\boldsymbol{x}_0^T \left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1} \boldsymbol{x}_0}}\sim t_{N-P-1}
\end{eqnarray}
[/math]
自由度[math]N-P-1[/math]の[math]t[/math]分布に従うことが分かります。この結果から予測区間を構成します。
重回帰モデルの予測区間
統計量[math]T[/math]が自由度[math]N-P-1[/math]の[math]t[/math]分布に従うことから信頼度[math](1-\alpha)[/math]の予測区間は[math] P_{lb}(\boldsymbol{x}_0)[/math]を
[math]
\begin{eqnarray}
\boldsymbol{\hat{\beta}}^T\boldsymbol{x}_0 – t_{N-P-1,\alpha/2}S\sqrt{1 + \boldsymbol{x}_0^T \left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1} \boldsymbol{x}_0}
\end{eqnarray}
[/math]
とし[math]P_{ub}(\boldsymbol{x}_0)[/math]を
[math]
\begin{eqnarray}
\boldsymbol{\hat{\beta}}^T\boldsymbol{x}_0 + t_{N-P-1,\alpha/2}S\sqrt{1 + \boldsymbol{x}_0^T \left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1} \boldsymbol{x}_0}
\end{eqnarray}
[/math]
として
[math]
P_{lb}(\boldsymbol{x}_0) \leq \boldsymbol{\beta}^T\boldsymbol{x}_0 \leq
P_{ub}(\boldsymbol{x}_0)
[/math]
で与えられます。慣習的に信頼度は[math]95\%, 99\%[/math]をとることが多いです。
最後に予測区間の意味や解釈の仕方、信頼区間との違いがややこしく誤解しやすいので自信のない方は「単回帰モデルの予測区間」も合わせて参照ください。
シリーズ記事
「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「重回帰」の性質を紹介しています。
ここでは誤差項が「独立同一な正規分布」に従うと仮定すると導ける性質として
- 最尤推定量: 最尤推定量は最小二乗推定量と一致。誤差分散に対する不偏推定量を導出。
- 誤差の正規性チェック
- 回帰係数、誤差分散の確率分布: 最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]と分散の不偏推定量[math]S^2[/math]の確率分布を導出
- 回帰係数の有意性: 最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]の確率分布と有意性検定を導出
- 信頼区間: 真の値の推定値が従う確率分布から信頼区間を導出
- 予測区間(本記事): 観測値が従う確率分布から予測区間を導出
を解説しています。
また行列やベクトル演算が多く何をしているか理解しづらいと感じた方は説明変数が1つの場合である「単回帰」も参照ください。