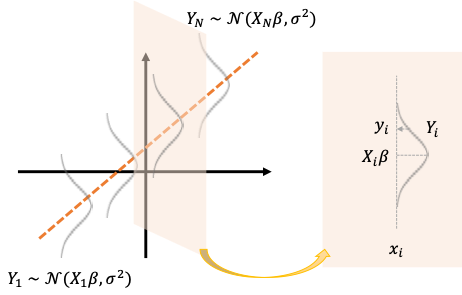
ここからは誤差項が正規分布に従うモデルを考えます。
[math]
\begin{eqnarray}
Y_i &=& \beta_0 + \beta_1 x_1 + \cdots + \beta_P x_P + \varepsilon_i \\
\varepsilon_i &\sim& \mathcal{N}(0, \sigma^2)
\end{eqnarray}
[/math]
具体的な確率分布を仮定するため最尤推定量を求めることができます。ここでは
- 回帰係数[math]\boldsymbol{\beta}[/math]の最尤推定量は最小二乗推定量と一致すること
- 分散[math]\sigma^2[/math]の最尤推定量をもとにした不偏推定量の導出
を示します。
確率モデル
表記をシンプルにするためこちらの記事で定義したベクトル、行列を使うと
[math]
\boldsymbol{Y} = \boldsymbol{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon},\ \boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0}, \sigma^2\boldsymbol{I})
[/math]
とかけます。
確率モデルは何が確率変数で何が確定値なのかわかりにくいのでまとめると
- [math]\boldsymbol{X},\ \boldsymbol{y}[/math]: 既知の確定値
- [math]\boldsymbol{\beta},\ \sigma^2[/math]: 未知の確定値
- [math]\boldsymbol{Y},\ \boldsymbol{\varepsilon}[/math]: 確率変数
になります。
なお、この確率モデルでは誤差が「無相関」かつ「分散一定」になるので「ガウス・マルコフの定理」が成立し最小二乗推定量は最良線形不偏推定量になります。
最尤推定量
確率変数[math]Y_i[/math]は仮定より独立で正規分布[math]\mathcal{N}(\boldsymbol{X}_i\boldsymbol{\beta}, \sigma^2)[/math]に従います。なお、[math]\boldsymbol{X}_i[/math]は行列[math]\boldsymbol{X}[/math]の[math]i[/math]行目を表します。
正規分布[math]\mathcal{N}(\mu, \sigma^2)[/math]の確率密度関数を[math]f(y|\mu, \sigma^2)[/math]とすると
[math]
f(y|\mu, \sigma^2) = \dfrac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\dfrac{(y – \mu)^2}{2\sigma^2}\right]
[/math]
で与えられます。これより対数尤度関数[math]\log L[/math]を求めると
[math]
\begin{eqnarray}
&& \log L(\boldsymbol{\beta}, \sigma^2 | \boldsymbol{y}) \\
&=& \log \prod_{i=1}^N f(y_i|\boldsymbol{X}_i\boldsymbol{\beta}, \sigma^2) \\
&=& -\dfrac{N}{2}\log \sigma^2-\dfrac{1}{2\sigma^2}\sum_{i=1}^N\left(y_i – \boldsymbol{X}_i\boldsymbol{\beta}\right)^2 + C \\
&=& -\dfrac{N}{2}\log \sigma^2-\dfrac{1}{2\sigma^2}\left(\boldsymbol{y} – \boldsymbol{X}\boldsymbol{\beta}\right)^T\left(\boldsymbol{y} – \boldsymbol{X}\boldsymbol{\beta}\right) + C
\end{eqnarray}
[/math]
となります。ここで[math]C[/math]は定数です。
尤度が最大になる[math]\boldsymbol{\beta}, \sigma^2[/math]を求めるために
[math]
\begin{cases}
\dfrac{\partial (\log L)}{\partial \boldsymbol{\beta}} = 0 \\
\dfrac{\partial (\log L)}{\partial \sigma^2} = 0
\end{cases}
[/math]
の第1式を整理すると
[math]
\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\beta} = \boldsymbol{X}^T\boldsymbol{y}
[/math]
と正規方程式が得られます。
したがって[math]\boldsymbol{\beta}[/math]の最尤推定量は最小二乗推定量と一致し
[math]
\boldsymbol{\hat{\beta}} = \left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T\boldsymbol{Y}
[/math]
で与えられます。
[math]\sigma^2[/math]の最尤推定量は[math]\partial (\log L)/ \partial \sigma^2 = 0[/math]を解いて
[math]
\hat{\sigma}^2 = \displaystyle\dfrac{1}{N}
\left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right)^T\left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right)
[/math]
で与えられます。
分散[math]\sigma^2[/math]の不偏推定量
不偏性を確認するため最尤推定量[math]\hat{\sigma}^2[/math]の期待値を求めます。
まず[math]H=\boldsymbol{X}(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T[/math]とすると「幾何学でみる重回帰の性質」でみたように[math]\boldsymbol{H}, \boldsymbol{I}-\boldsymbol{H}[/math]はそれぞれ[math]\boldsymbol{X}, \boldsymbol{X}^\perp[/math]が張る空間への射影になっており
[math]
\begin{eqnarray}
&& \boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}} \\
&=& \boldsymbol{Y} – \boldsymbol{X}\left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T\boldsymbol{Y} \\
&=& \left(\boldsymbol{I}-\boldsymbol{H}\right)\boldsymbol{Y} \\
&=& \left(\boldsymbol{I}-\boldsymbol{H}\right)\left(\boldsymbol{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}\right) \\
&=& \left(\boldsymbol{I}-\boldsymbol{H}\right)\boldsymbol{\varepsilon}
\end{eqnarray}
[/math]
と整理できます。これより
[math]
\begin{eqnarray}
&& \left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right)^T\left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right) \\
&=& \boldsymbol{\varepsilon}^T\left(\boldsymbol{I}-\boldsymbol{H}\right)\boldsymbol{\varepsilon} \\
&=& {\rm tr}\left[\left(\boldsymbol{I}-\boldsymbol{H}\right)\boldsymbol{\varepsilon}\boldsymbol{\varepsilon}^T\right]
\end{eqnarray}
[/math]
となります。最後の式変形は[math]\boldsymbol{x}^TA\boldsymbol{x}={\rm tr}\left[A\boldsymbol{x}\boldsymbol{x}^T\right][/math]とかけることを利用しています。よって
[math]
\begin{eqnarray}
E\left[\hat{\sigma}^2\right] &=& \dfrac{1}{N}{\rm tr}\left[\left(\boldsymbol{I}-\boldsymbol{H}\right)E\left[\boldsymbol{\varepsilon}\boldsymbol{\varepsilon}^T\right]\right] \\
&=& \sigma^2{\rm tr}\left[\left(\boldsymbol{I}-\boldsymbol{H}\right)\right]
\end{eqnarray}
[/math]
となり[math]{\rm tr}\left[AB\right]={\rm tr}\left[BA\right][/math]なので
[math]
\begin{eqnarray}
{\rm tr}\left[H\right] &=&
{\rm tr}\left[\boldsymbol{X}(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\right] \\
&=&
{\rm tr}\left[(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{X}\right] \\
&=&
{\rm tr}\left[\boldsymbol{I}_{P+1}\right] \\
&=& P+1
\end{eqnarray}
[/math]
となります。ここで[math]\boldsymbol{I}_{n}[/math]は[math]n\times n[/math]の単位行列を表します。以上より
[math]
E\left[\hat{\sigma}^2\right] = \dfrac{N-P-1}{N}\sigma^2
[/math]
となり少し小さな推定になっており不偏性を持たないことがわかります。
そこで、回帰係数の検定や信頼区間、予測区間の導出では分散[math]\sigma^2[/math]の不偏推定量を
[math]
S^2 = \displaystyle\dfrac{1}{N-P-1}
\left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right)^T\left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right)
[/math]
で定義し分散[math]\sigma^2[/math]の推定量として用います。
シリーズ記事
「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「重回帰」の性質を紹介しています。
ここでは誤差項が「独立同一な正規分布」に従うと仮定すると導ける性質として
- 最尤推定量(本記事): 最尤推定量は最小二乗推定量と一致。誤差分散に対する不偏推定量を導出。
- 誤差の正規性チェック
- 回帰係数、誤差分散の確率分布: 最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]と分散の不偏推定量[math]S^2[/math]の確率分布を導出
- 回帰係数の有意性: 最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]の確率分布と有意性検定を導出
- 信頼区間: 真の値の推定値が従う確率分布から信頼区間を導出
- 予測区間: 観測値が従う確率分布から予測区間を導出
を解説しています。
また行列やベクトル演算が多く何をしているか理解しづらいと感じた方は説明変数が1つの場合である「単回帰」も参照ください。