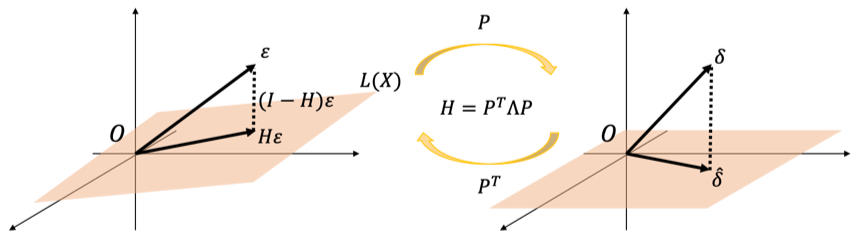誤差項が独立同一な正規分布に従う場合
- 最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]が正規分布に従う
- 分散の不偏推定量[math]S^2[/math]に対し[math](N-P-1)S^2/\sigma^2[/math]は[math]\chi^2[/math]分布に従う
- 最小二乗推定量と分散不偏推定量は独立
ことが示せます。回帰係数の検定や信頼区間、予測区間を導出する際に中核となる事実で重回帰モデル解析のクライマックスと言えると思います。
証明にあたっては重回帰モデルを幾何的にみて射影や直交変換をうまく使う必要があるため「幾何学でみる重回帰の性質」も事前に参照ください。
確率モデル
表記をシンプルにするためこちらの記事で定義したベクトル、行列を使うと
[math]
\boldsymbol{Y} = \boldsymbol{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon},\ \boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0}, \sigma^2\boldsymbol{I}_N)
[/math]
とかけます。なお、本記事ではサイズの異なる単位行列が出てくるため[math]n\times n[/math]の単位行列を[math]I_n[/math]と表記します。
確率モデルは何が確率変数で何が確定値なのかわかりにくいのでまとめると
- [math]\boldsymbol{X},\ \boldsymbol{y}[/math]: 既知の確定値
- [math]\boldsymbol{\beta},\ \sigma^2[/math]: 未知の確定値
- [math]\boldsymbol{Y},\ \boldsymbol{\varepsilon}[/math]: 確率変数
になります。
最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]と分散の不偏推定量[math]S^2[/math]の確率分布
誤差項が独立同一な正規分布に従う場合、最小二乗推定量[math]\boldsymbol{\hat{\beta}}=\left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T\boldsymbol{Y}[/math]と分散の不偏推定量[math]S^2=\frac{1}{N-P-1} \left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right)^T\left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right)[/math]の確率分布を求めることができます。
- [math]\boldsymbol{\hat{\beta}}\sim \mathcal{N}\left(\boldsymbol{\beta}, \sigma^2(\boldsymbol{X}^T\boldsymbol{X})^{-1}\right)[/math]
- [math]\frac{(N-P-1)S^2}{\sigma^2} \sim \chi^2_{N-P-1}[/math]
- [math]\boldsymbol{\hat{\beta}}[/math]と[math]S^2[/math]は独立
証明のアウトライン
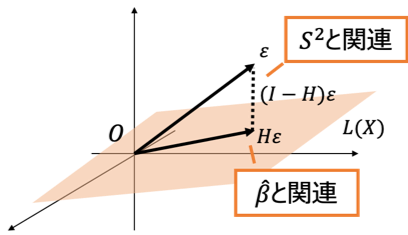
[math]\boldsymbol{\varepsilon}(=\boldsymbol{Y}-\boldsymbol{X}\boldsymbol{\beta})[/math]を[math]\boldsymbol{X}[/math]の張る空間に射影した時に
- 射影した点[math]\boldsymbol{H}\boldsymbol{\varepsilon}[/math]は[math]\boldsymbol{\hat{\beta}}[/math]と関連
- [math]\boldsymbol{\varepsilon}[/math]と射影した点との距離[math]\|(\boldsymbol{I}_N-\boldsymbol{H})\boldsymbol{\varepsilon}\|[/math]は[math]S^2[/math]と関連
があることに着目します。証明のキーアイディアは射影行列[math]\boldsymbol{H}=\boldsymbol{X}(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T[/math]を対角化し直交変換した空間で考えると
- 点[math]\boldsymbol{\varepsilon}[/math]を変換した点[math]\boldsymbol{\delta}[/math]も正規分布[math]\mathcal{N}(\boldsymbol{0}, \sigma^2\boldsymbol{I}_N)[/math]に従う
- 射影[math]\boldsymbol{H},\ \boldsymbol{I}_N-\boldsymbol{H}[/math]はそれぞれベクトル成分の取り出しに対応
- [math]\boldsymbol{\delta}=(\boldsymbol{\delta}_1, \boldsymbol{\delta}_2)^T[/math]とした時に射影した点は[math]\boldsymbol{\delta}_1[/math]のみ、距離は[math]\boldsymbol{\delta}_2[/math]のみに依存し独立
ということが分かります。あとは元の空間に戻して[math]\boldsymbol{\hat{\beta}}, S^2[/math]との関係を評価することで確率分布を求めることができます。それでは順に見ていきましょう。
射影した点と[math]\boldsymbol{\hat{\beta}}, S^2[/math]の関係
まず点[math]\boldsymbol{\varepsilon}[/math]を射影した点は
[math]
\begin{eqnarray}
\boldsymbol{H}\boldsymbol{\varepsilon} &=& \boldsymbol{X}(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T(\boldsymbol{Y}-\boldsymbol{X}\boldsymbol{\beta}) \\
&=& \boldsymbol{X}(\boldsymbol{\hat{\beta}} – \boldsymbol{\beta})
\end{eqnarray}
[/math]
とかけます。また[math]\boldsymbol{\varepsilon}[/math]と射影した点との距離[math]\|(\boldsymbol{I}_N-\boldsymbol{H})\boldsymbol{\varepsilon}\|[/math]はこちらの記事の「分散の不偏推定量」でみたように[math]\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}=\left(\boldsymbol{I}_N-\boldsymbol{H}\right)\boldsymbol{\varepsilon}[/math]なので
[math]
\begin{eqnarray}
\|(\boldsymbol{I}_N-\boldsymbol{H})\boldsymbol{\varepsilon}\|^2 &=& \|\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\|^2 \\
&=& (N-P-1)S^2
\end{eqnarray}
[/math]
とそれぞれ関連づけることができます。
射影行列[math]\boldsymbol{H}[/math]の対角化
射影行列[math]\boldsymbol{H}[/math]は実対称行列なので直交行列[math]\boldsymbol{P}[/math]を用いて対角化できます。
[math]
\boldsymbol{H} = \boldsymbol{P}^T\boldsymbol{\Lambda}\boldsymbol{P}
[/math]
対角行列を求めるために固有値を調べます。[math]\boldsymbol{H}[/math]の固有値と固有ベクトルを[math]\lambda, \boldsymbol{v}[/math]とすると射影行列の性質[math]\boldsymbol{H}^2=\boldsymbol{H}[/math]より
[math]
\begin{eqnarray}
\lambda \boldsymbol{v} &=& \boldsymbol{H}\boldsymbol{v} \\
&=& \boldsymbol{H}^2\boldsymbol{v} \\
&=&
\lambda^2 \boldsymbol{v}
\end{eqnarray}
[/math]
より[math] \lambda= \lambda^2[/math]なので固有値は[math]0[/math]または[math]1[/math]になります。さらに[math]{\rm rank}\ H= P+1[/math]なので
[math]
\boldsymbol{H} = \boldsymbol{P}^T
\begin{pmatrix}
\boldsymbol{I}_{P+1} & \boldsymbol{O} \\
\boldsymbol{O} & \boldsymbol{O}
\end{pmatrix}
\boldsymbol{P}
[/math]
と対角化できることが分かります。あわせて直交成分への射影[math] \boldsymbol{I}_N- \boldsymbol{H}[/math]も
[math]
\boldsymbol{I}_N-
\boldsymbol{H} = \boldsymbol{P}^T
\begin{pmatrix}
\boldsymbol{O} & \boldsymbol{O} \\
\boldsymbol{O} & \boldsymbol{I}_{N-P-1}
\end{pmatrix}
\boldsymbol{P}
[/math]
と対角化されます。
正規分布に従う確率変数の直交変換
ここからは直交行列[math]\boldsymbol{P}[/math]で変換した空間で考えます。
まず点[math]\boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0}, \sigma^2\boldsymbol{I}_N)[/math]を直交変換した[math]\boldsymbol{\delta}=\boldsymbol{P}\boldsymbol{\varepsilon}[/math]の確率分布を求めます。
多次元正規分布に従う確率変数の線形変換に関する次の結果を利用します。
この結果より
[math]
\begin{eqnarray}
\boldsymbol{\delta} &=& \boldsymbol{P}\boldsymbol{\varepsilon} \\
&\sim& \mathcal{N}(\boldsymbol{0}, \sigma^2\boldsymbol{P}\boldsymbol{I}_N\boldsymbol{P}^T) \\
&\sim& \mathcal{N}(\boldsymbol{0}, \sigma^2\boldsymbol{I}_N)
\end{eqnarray}
[/math]
と直交変換した点[math] \boldsymbol{\delta}[/math]も分布[math]\mathcal{N}(\boldsymbol{0}, \sigma^2\boldsymbol{I}_N)[/math]に従うことが分かります。
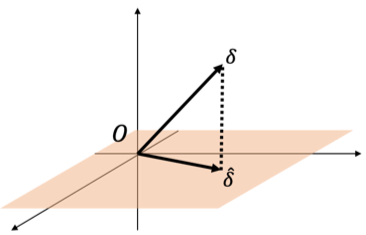
射影した点および距離が従う確率分布
直交変換した空間では射影[math] \boldsymbol{H}[/math]は
[math]
\boldsymbol{\Lambda}=\begin{pmatrix}
\boldsymbol{I}_{P+1} & \boldsymbol{O} \\
\boldsymbol{O} & \boldsymbol{O}
\end{pmatrix}
[/math]
になるので[math]N[/math]次元のベクトルの第[math]1[/math]〜[math]P+1[/math]成分を抜き出すことに対応します。つまり[math]\boldsymbol{\delta}=(\boldsymbol{\delta}_1 \boldsymbol{\delta}_2),\ \boldsymbol{\delta}_1\in\mathbb{R}^{P+1}, \boldsymbol{\delta}_2\in\mathbb{R}^{N-P-1}[/math]と分けた時に点[math]\boldsymbol{\delta}[/math]を射影した点[math]\boldsymbol{\Lambda} \boldsymbol{\delta}[/math]は
[math]
\boldsymbol{
\Lambda} \boldsymbol{\delta} = \begin{pmatrix}
\boldsymbol{\delta}_1 \\
\boldsymbol{0}
\end{pmatrix}
[/math]
となり点[math]\boldsymbol{\delta}[/math]との距離は
[math]
\begin{eqnarray}
\|(\boldsymbol{
I}_N-\boldsymbol{
\Lambda})\boldsymbol{\delta}\| &=&
\left\|
\begin{pmatrix}
\boldsymbol{0} \\
\boldsymbol{\delta}_2
\end{pmatrix} \right\| \\
&=& \|\boldsymbol{\delta}_2\|
\end{eqnarray}
[/math]
となります。これより
- 点[math]\boldsymbol{\delta}[/math]を射影した点は[math](\boldsymbol{\delta}_1 \boldsymbol{0})^T[/math]で[math]\boldsymbol{\delta}_1[/math]は[math]\mathcal{N}(\boldsymbol{0}, \sigma^2\boldsymbol{I}_{P+1})[/math]に従う
- 点[math]\boldsymbol{\delta}[/math]と射影した点との距離に関して[math] \|(\boldsymbol{ I}_N-\boldsymbol{ \Lambda})\boldsymbol{\delta}\|^2 / \sigma^2 = \|\boldsymbol{\delta}_2 / \sigma\|^2[/math]は[math]\chi^2_{N-P-1}[/math]に従う
- 点[math]\boldsymbol{\delta}[/math]を射影した点[math]\boldsymbol{\Lambda} \boldsymbol{\delta}[/math]は[math]\boldsymbol{\delta}_1[/math]のみに依存し、距離は[math]\boldsymbol{\delta}_2[/math]のみに依存するため独立
であることがわかります。直交変換した空間で求めたい結論が得られたので元の空間に戻して評価します。
最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]と分散の不偏推定量[math]S^2[/math]の確率分布
直交行列[math]\boldsymbol{P}[/math]を[math](P+1)[/math]行[math]N[/math]列の行列[math]\boldsymbol{P}_1[/math]と[math](N-P-1)[/math]行[math]N[/math]列の行列[math]\boldsymbol{P}_2[/math]に分けます。
[math]
\boldsymbol{P} =
\begin{pmatrix}
\boldsymbol{P}_1 \\
\boldsymbol{P}_2
\end{pmatrix}
[/math]
点[math]\boldsymbol{\varepsilon}[/math]を射影した点は
[math]
\begin{eqnarray}
\boldsymbol{H}\boldsymbol{\varepsilon} &=& \boldsymbol{P}^T \boldsymbol{\delta} \\
&=& \left(\boldsymbol{P}_1^T \boldsymbol{P}_2^T\right)
\begin{pmatrix}
\boldsymbol{\delta}_1 \\
\boldsymbol{0}
\end{pmatrix} \\
&=& \boldsymbol{P}_1^T\boldsymbol{\delta}_1
\end{eqnarray}
[/math]
とかけます。ここで[math] \boldsymbol{H} = \boldsymbol{P}^T\boldsymbol{\Lambda}\boldsymbol{P}=\boldsymbol{P}_1^T\boldsymbol{P}_1[/math]より
[math]
\boldsymbol{P}_1 = (\boldsymbol{X}^T\boldsymbol{X})^{-1/2}\boldsymbol{X}^T
[/math]
と求めることができ[math] \boldsymbol{H}\boldsymbol{\varepsilon} = \boldsymbol{X}(\boldsymbol{\hat{\beta}} – \boldsymbol{\beta})[/math]と書けることと合わせて整理すると
[math]
\begin{eqnarray}
\boldsymbol{\hat{\beta}} &=& \boldsymbol{\beta} + (\boldsymbol{X}^T\boldsymbol{X})^{-1/2}\boldsymbol{\delta}_1 \\
&\sim & \mathcal{N}\left(\boldsymbol{\beta}, \sigma^2(\boldsymbol{X}^T\boldsymbol{X})^{-1}\right)
\end{eqnarray}
[/math]
が成立します。
次に距離に関しても直交変換は距離に関して不変なので
[math]
\begin{eqnarray}
\dfrac{(N-P-1)S^2}{\sigma^2} &=&
\dfrac{
\|(\boldsymbol{I}_N-\boldsymbol{H})\boldsymbol{\varepsilon}\|^2}{\sigma^2} \\
&=& \dfrac{\|(\boldsymbol{
I}_N-\boldsymbol{
\Lambda})\boldsymbol{\delta}\|^2}{\sigma^2} \\
&=& \left\| \frac{\boldsymbol{\delta}_2}{\sigma} \right\|^2 \\
&\sim & \chi^2_{N-P-1}
\end{eqnarray}
[/math]
が成立します。
以上より
- [math]\boldsymbol{\hat{\beta}}\sim \mathcal{N}\left(\boldsymbol{\beta}, \sigma^2(\boldsymbol{X}^T\boldsymbol{X})^{-1}\right)[/math]
- [math]\frac{(N-P-1)S^2}{\sigma^2} \sim \chi^2_{N-P-1}[/math]
- [math]\boldsymbol{\hat{\beta}}[/math]と[math]S^2[/math]は独立
が成立することが示されました。
この事実を使って回帰係数の検定、信頼区間や予測区間を導出することができます。
シリーズ記事
「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「重回帰」の性質を紹介しています。
ここでは誤差項が「独立同一な正規分布」に従うと仮定すると導ける性質として
- 最尤推定量: 最尤推定量は最小二乗推定量と一致。誤差分散に対する不偏推定量を導出。
- 誤差の正規性チェック
- 回帰係数、誤差分散の確率分布(本記事): 最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]と分散の不偏推定量[math]S^2[/math]の確率分布を導出
- 回帰係数の有意性: 最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]の確率分布と有意性検定を導出
- 信頼区間: 真の値の推定値が従う確率分布から信頼区間を導出
- 予測区間: 観測値が従う確率分布から予測区間を導出
を解説しています。
また行列やベクトル演算が多く何をしているか理解しづらいと感じた方は説明変数が1つの場合である「単回帰」も参照ください。