重回帰モデルでの回帰係数の有意性検定

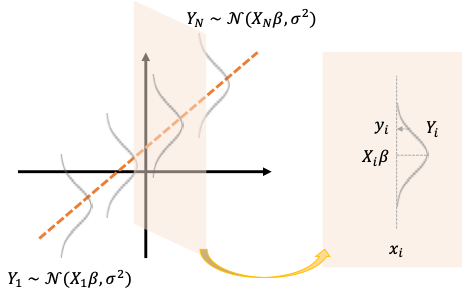
誤差項が独立同一な正規分布に従う場合、「回帰係数の確率分布」で見たように最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]と誤差項の分散[math]\sigma^2[/math]の不偏推定量[math]S^2[/math]について

• [math]\boldsymbol{\hat{\beta}}\sim \mathcal{N}\left(\boldsymbol{\beta}, \sigma^2(\boldsymbol{X}^T\boldsymbol{X})^{-1}\right)[/math]
• [math]\frac{(N-P-1)S^2}{\sigma^2} \sim \chi^2_{N-P-1}[/math]
• [math]\boldsymbol{\hat{\beta}}[/math]と[math]S^2[/math]は独立

が成立します。この事実を使って「回帰係数の有意性検定」として知られる[math]t[/math]分布を使った検定を導くことができます。

確率モデル

表記をシンプルにするためこちらの記事で定義したベクトル、行列を使うと

[math]
\boldsymbol{Y} = \boldsymbol{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon},\ \boldsymbol{\varepsilon}\sim \mathcal{N}(\boldsymbol{0}, \sigma^2\boldsymbol{I}_N)
[/math]

とかけます。

確率モデルは何が確率変数で何が確定値なのかわかりにくいのでまとめると

• [math]\boldsymbol{X},\ \boldsymbol{y}[/math]: 既知の確定値
• [math]\boldsymbol{\beta},\ \sigma^2[/math]: 未知の確定値
• [math]\boldsymbol{Y},\ \boldsymbol{\varepsilon}[/math]: 確率変数

になります。

最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]と分散の不偏推定量[math]S^2[/math]の確率分布

誤差項が独立同一な正規分布に従う場合、最小二乗推定量[math]\boldsymbol{\hat{\beta}}=\left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T\boldsymbol{Y}[/math]と分散[math]\sigma^2[/math]の不偏推定量[math]S^2=\frac{1}{N-P-1}
\left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right)^T\left(\boldsymbol{Y} – \boldsymbol{X}\boldsymbol{\hat{\beta}}\right)[/math]の確率分布を求めることができます。

この事実から「回帰係数の有意性検定」を導くことができます。

回帰係数の有意性検定

[math](\boldsymbol{X}^T\boldsymbol{X})^{-1}[/math]の第[math](i, i)[/math]成分を[math]a_{i,i}[/math]と書くと回帰係数[math]\hat{\beta}_i[/math]は[math]\mathcal{N}(\beta_i, \sigma^2 a_{i+1,i+1})[/math]に従います^[1][math]\hat{\beta}_i[/math]の添字は0から始まり[math](\boldsymbol{X}^T\boldsymbol{X})^{-1}[/math]の添字は1から始まるため対応する添字が1つずれます。。これより統計量[math]T_{\beta_i}[/math]が

[math]
\begin{eqnarray}


T_{\beta_i} &=& \dfrac{\frac{\hat{\beta}_i – \beta_i}{\sqrt{\sigma^2 a_{i+1,i+1}}}}{\sqrt{\frac{(N-P-1)S^2}{\sigma^2}\cdot \frac{1}{N-P-1}}} \\
&=& \dfrac{\hat{\beta}_i – \beta_i}{\sqrt{a_{i+1,i+1}S^2}}\sim t_{N-P-1}
\end{eqnarray}
[/math]

自由度[math]N-P-1[/math]の[math]t[/math]分布に従うことが分かります。この分母を[math]\hat{\beta}_i[/math]の標準誤差(Standard Error)と呼び[math]s.e.(\hat{\beta}_i)[/math]と表記します。

[math]

s.e.(\hat{\beta}_i) = \sqrt{a_{i+1,i+1}S^2}
[/math]

回帰係数の有意性検定

回帰モデルを作る目的の1つは

説明変数[math]x_i[/math]が目的変数[math]y[/math]の予測に寄与するかどうか

を明らかにすることです。予測に寄与しない場合、[math]\beta_i=0[/math]になると考えられるので

• 帰無仮説[math]H_0[/math]: [math]\beta_i=0[/math]
• 対立仮説[math]H_1[/math]: [math]\beta_i\ne 0[/math]

を適当な有意水準[math]\alpha[/math]で検定し寄与の有無を判断できます。この検定を「回帰係数の有意性検定」と呼びます。

回帰係数[math]\hat{\beta}_i[/math]の有意性検定の手順は以下になります。

1. 事前に有意水準[math]\alpha[/math]を決め棄却域[math]R = \left\{t\ |\ |t-0| > t_{N-P-1, \alpha/2} \right\}[/math]を求める
2. 統計量[math]

T_{\beta_i}=\dfrac{\hat{\beta}_i – 0}{\sqrt{a_{i+1,i+1}S^2}}[/math]を計算する
3. [math]T_{\beta_i} \in R[/math]ならば帰無仮説を棄却し、そうでないなら帰無仮説を採択する

シリーズ記事

「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「重回帰」の性質を紹介しています。

ここでは誤差項が「独立同一な正規分布」に従うと仮定すると導ける性質として

• 最尤推定量は最小二乗推定量と一致。誤差分散に対する不偏推定量を導出。
• 誤差の正規性チェック
• 最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]と分散の不偏推定量[math]S^2[/math]の確率分布を導出
• 回帰係数の有意性（本記事）: 最小二乗推定量[math]\boldsymbol{\hat{\beta}}[/math]の確率分布と有意性検定を導出
• 信頼区間: 真の値の推定値が従う確率分布から信頼区間を導出
• 予測区間: 観測値が従う確率分布から予測区間を導出

を解説しています。

また行列やベクトル演算が多く何をしているか理解しづらいと感じた方は説明変数が1つの場合である「単回帰」も参照ください。