前回の記事ではロジスティック回帰モデルで生存者予測を行いました。
ロジスティック回帰モデルは「目的変数(生存しやすさ)を特徴量の重み付けで表現しモデルの可読性が高い」という利点がある一方で
目的変数と特徴量の間には「単調」で「独立」な関係があると仮定
しているので
- 特徴量の増加に対し生存率が上下する場合は特徴量の加工が必要
- 特徴量の組合せで現れる交互作用[1]例えば「年齢が5〜15才」の生存率が「チケットクラス」で異なったように複数の特徴量の組合せで現れる効果を交互作用と呼びます。を考慮するには個別に特徴量化が必要
で、精度向上などで特徴量を追加する作業が大変になることが多いです。
そこで非単調性や交互作用がある場合でも学習の中で自然とその関係性を見つけてくれるモデルとして知られる「Random Forest」を使っていくことにします。
Random Forestモデルとは
Random Forestは多数の決定木モデルを使って予測を行うモデルです。
まずRandom Forestを構成している決定木の概要と性質を簡単に紹介します。
決定木モデル
決定木は学習データから「性別=男性 かつ チケットクラス=3rdならば生存率が低い」といった条件の組合せで生存率の高い/低い集団に分割する手法です。
実際に決定木モデルを構築してみると

が得られます。集団を特定する条件が木構造で表現[2]各ノードが分岐条件を表し左の枝がYesの場合、右の枝がNoの場合のパスを示します。されており
- 「男性」かつ「運賃が26.269以下」の場合は死亡率が高い
- 「女性」かつ「チケットクラスが1st or 2nd」の場合は生存率が高い
といった集団を学習データから抽出できています。
決定木の性質として
- 特徴量の増加に対し生存率が上下する場合も条件の組合せで表現可能
- 特徴量の組合せ(交互作用)も表現可能
のため特徴量を加工、追加しなくても学習の中で関係性を見つけてくれることが期待できます。一方、非常にシンプルなモデルのため精度には限界があります[3]実際、決定木でTitanic生存者予測を行うとロジスティック回帰を少し下回る精度になることが多いです。。
Random Forest
決定木の特性を維持しつつ精度向上を実現したモデルがRandom Forestモデルです。Random Forestモデルでは
- 学習データからサンプルデータと特徴量をランダムサンプリング
- ランダムサンプリングしたデータで決定木を作る
- 上記を[math]B[/math]回繰り返す
- [math]B[/math]個の決定木の出力の平均値を予測値として出力する
を行います。Random Forestのポイントは
サンプルデータ(行データ)も特徴量(列データ)もランダムサンプリングする
ことです。一見、決定木用データの情報量が少なくなりそうですが各決定木間の相関が小さくなり全体として精度が向上することが知られています。
Random Forestモデルの構築
ここからRandom Forestモデルの構築を行います。記事は主要なポイントに絞って書いており細かな点や実装はGitHubのコードも参照ください。また、効率的なパラメタチューニングについては「GridSearchCVによるチューニング」も合わせて参照ください。
前処理
決定木は「特徴量の値が閾値を上回った/下回った」で条件分岐していくので外れ値の影響を受けにくくロジスティック回帰では考慮した外れ値処理は行いません。
また、カテゴリデータはロジスティック回帰と同様に数値データに変換する必要があります。ロジスティック回帰ではダミー変数化しましたがRandom Forestは特徴量をランダムサンプリングするためダミー変数化より特徴量の次元を増やさない方法の方が学習がうまく行きやすいです。
今回は「カテゴリの値」を「カテゴリの値の出現回数の順位」に変換するLabel count rank encodingで数値化しました。例えば乗船港(Embarked)はC, Q, Sの3つの値がありそれぞれ出現回数の順位C=2, Q=3, S=1に変換されます。
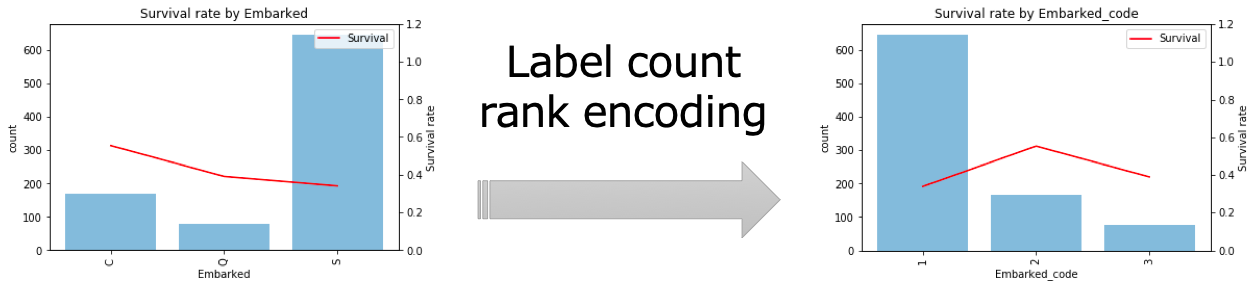
上記のようにアルゴリズムの特性に応じて外れ値処理の要否やカテゴリ変数の変換方法を適切に決める必要があります。機械学習の難しいところでもあり、うまくアルゴリズムにあった前処理にすると精度を向上できるという面白いところでもあります。
ハイパーパラメタチューニング
Random Forestモデルは大きく
- 決定木に関するハイパーパラメタ
- 木の深さ
- ノードの分割基準など
- 全体挙動に関するハイパーパラメタ
- 決定木の数
- ランダムサンプリングの方法など
があります。多くの特徴量をまとめてチューニングすると組合せ爆発が起こるのでまずが主要なパラメタからチューニングするのが鉄則で
- 決定木の数(n_estimators)
- ランダムサンプリングする特徴量数(max_features)
- 決定木の深さ(max_depth)
をチューニングします。scikit-learnのドキュメントを参考にデフォルト値付近で最初は大きな範囲でパラメタを刻んで、徐々に細かく刻むようにします。また、「機械学習モデルのデータ分割/評価方法」で紹介した交差検証で精度を評価するようにします。
今回のチューニングではLogLossが一番低くなるパラメタとして
- 決定木の数(n_estimators): 50
- ランダムサンプリングする特徴量数(max_features): 2
- 決定木の深さ(max_depth): 7
が得られました。
モデル確認
Random Forestモデルでは「特徴量がどれだけ精度に寄与したか」を表すFeature Importanceという指標を確認することができます。
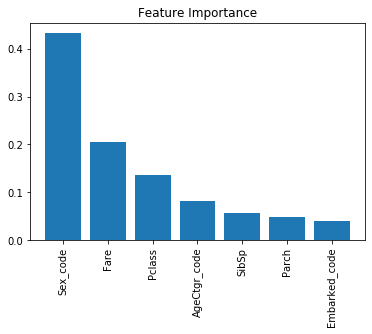
確認すると「性別」「運賃」「チケットクラス」「年齢」などの項目が上位にきており探索的データ解析とも合致する結果になっています。
検証データで生存/死亡者の生存確率を推定しヒストグラムをとったのが下図です。
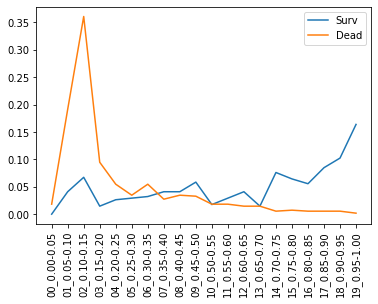
- 生存者(青線)は確かに0.50より大きい領域に偏っている
- 死亡者(オレンジ線)は0.20未満に偏っている
- 0.15-0.20の領域の生存者も5%程度になりロジスティック回帰より改善
とロジスティック回帰より良さそうです。
実際、検証データの精度は0.806とロジスティック回帰と変わらないのですがLogLossはロジスティック回帰の0.443から0.429に少し改善しました。決定木単体だとロジスティック回帰より精度面は少し劣るのですが、ランダムサンプリングして平均をとるだけでロジスティック回帰を上回るのは面白いですね。
評価結果
構築したモデルでテストデータを予測しSubmitすると精度は0.775になりました。評価結果をまとめると
- 交差検証でのLogLoss: 0.429
- 交差検証での精度: 0.806
- テストデータでの精度: 0.775
になります。
ロジスティック回帰の精度と変わらない結果になりましたが、Random Forestの方が特徴量エンジニアリングと呼ばれる特徴量の追加、変換が楽なのでRandom Forestモデルで特徴量の改良を行っていきます。