ベースラインモデル編では「Majority classifier」を構築しました。Majority classifierは特徴量を1つも用いずすべて「死亡」と予測するモデルでしたが、ここでは特徴量を1つだけ用いる単変量モデルを作っていきましょう。
単変量モデルの精度を評価することで
- 特徴量ごとのベースライン(精度62.7%)からの精度向上
- 学習/テストデータにおける各特徴量と生存率の関係
を把握し、予測に有用な特徴量やテストデータでの傾向を把握することができます。
単変量モデル
単変量モデルとして代表的な2値分類モデルであるロジスティック回帰モデルを用います。以下の特徴量をそれぞれ個別に用いてモデルを構築し、精度を評価します。
- チケットのクラス(Pclass)
- 性別(Sex)
- 年齢(Age)
- 一緒に乗船した兄弟、配偶者の数(SibSp)
- 一緒に乗船した親子の数(Parch)
- 運賃(Fare)
- 乗船港(Embarked)
ロジスティック回帰モデル
ロジスティック回帰モデルは特徴量を[math]x_1,\dots,x_P[/math]とし
[math]
y = \dfrac{1}{1+\exp\left[-(a_0+a_1x_1+\cdots+a_Px_P) \right]}
[/math]
で表されます。ここで[math]a_0,\dots,a_P[/math]は回帰係数です。
Scikit-learnでは学習データの特徴量をX_train, 目的変数をy_trainとして
from sklearn.linear_model import LogisticRegression model = LogisticRegression(penalty='none') model.fit(X_train, y_train)
でモデルを構築することができます。なお、デフォルトでは過学習を避けるため「正則化」を行う設定になっていますが、今回は単変量モデルで過学習のリスクは低いためpenalty=’none’として正則化を行わないロジスティック回帰を用います。
本記事に対応するコードもGitHubにアップしているので合わせてご参照ください。
チケットのクラス(Pclass)モデル
クロス集計(前半)でみた通りチケットクラスが上がるにつれて生存率が上がるので今回はそのまま順序尺度データとして使ってモデルを作ります。
当てはまりを確認すると
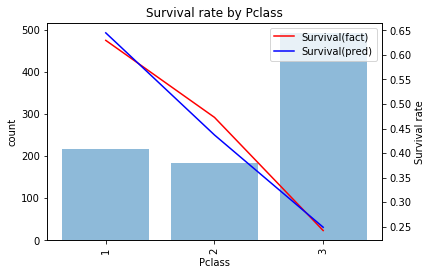
とうまく当てはまっており学習データでの精度は0.679になります。予測結果を見ると
- 1stなら生存
- 2nd, 3rdなら死亡
と予測するモデルになっています。このモデルでテストデータを予測しSubmitすると精度は0.656と学習データと比べ少し精度が低いことがわかります。
性別モデル
性別データはフラグデータなのでダミー変数化して使います。この際、ダミー変数化した変数を1つ削る(残りのダミー変数から決定できるため)必要があるのですが
最頻値に対応するダミー変数を削る
ことをオススメします。各ダミー変数の回帰係数が「最もメジャーな値」から「別の値」に変わった際の差分をあらわすようになりイメージがしやすくなると思います。
ここでは最頻値である男性に対応するダミー変数を削って女性かどうかを表すダミー変数を使っています。当てはまりを確認すると
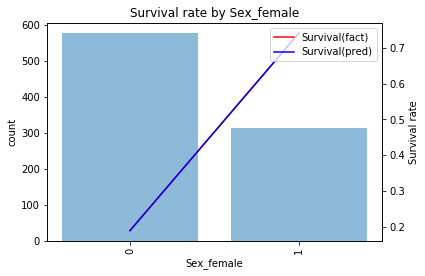
ときれいに当てはまっており学習データでの精度は0.787になります。予測結果を見ると
- 女性なら生存
- 男性なら死亡
と予測するモデルになっています。このモデルでテストデータを予測しSubmitすると精度は0.766と学習データと比べ少し精度が下がることがわかります。
年齢モデル
クロス集計(前半)を踏まえ年齢だけではなくチケットクラスも考慮し
- 5才以下
- 5〜15才(2nd以上)
- 5〜10才(3rd)
- 10〜15才(3rd)
- 15〜60才
- 60才以上
- 欠損値
- 推定値
のカテゴリに分けます。
当てはまりを確認すると
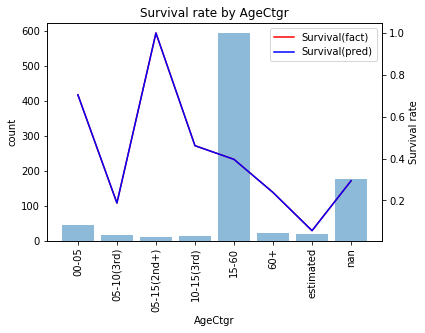
ときれいに当てはまっており学習データでの精度は0.646になります。予測結果を見ると
- 「5才以下」「5〜15才(2nd以上)」を生存
- それ以外を死亡
と予測するモデルになっています。このモデルでテストデータを予測、submitすると精度0.627と残念ながらMajority classifierと同じ精度しか出ていないことがわかります。
一緒に乗船した兄弟、配偶者の数(SibSp)モデル
クロス集計(後半)でみたように「SibSp」と「SibSp=0フラグ」を使うようにします。またSibSpは4以上はサンプル数が少ないので4に丸めて使います。
当てはまりを確認すると

とうまく当てはまっており学習データでの精度は0.633になります。予測結果を見ると
- SibSp=1なら生存
- それ以外を死亡
と予測するモデルになっています。このモデルでテストデータを予測、submitすると精度0.617と残念ながらMajority classifierを下回ることがわかります。
一緒に乗船した親子の数(Parch)モデル
SibSpモデルと同様に「Parch=0」フラグを作り3以上を丸めて使います。
当てはまりを確認すると
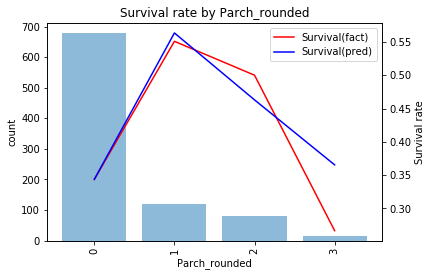
とうまく当てはまっており学習データでの精度は0.630になります。予測結果を見ると
- Parch=1なら生存
- それ以外を死亡
と予測するモデルになっています。このモデルでテストデータを予測、submitすると精度0.675と学習データより精度が高くなることがわかります。
運賃(Fare)モデル
運賃は裾が長い分布なので80以上(概ね上位[math]10\%[/math]点)は80に丸めて使います。
当てはまりを確認すると
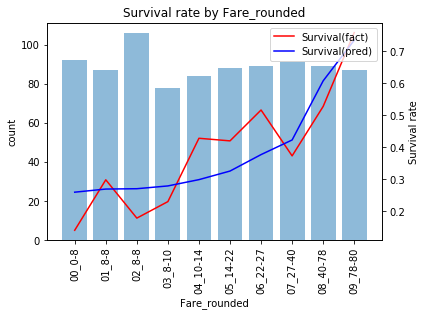
と少しずれはあるものの概ね当てはまっています。学習データでの精度は0.673になります。予測結果を見ると
- 運賃が46.9以上で生存
- それ以外を死亡
と予測するモデルになっています。このモデルでテストデータを予測、submitすると精度0.646と学習データと比べ精度が低いことがわかります。
乗船港(Embarked)モデル
最後に乗船港を使ってモデルを作ります。予測結果を見ると
- Cなら生存
- S, Qなら死亡
となっており学習データでもテストデータでも精度0.636とMajority classifierと比べ少し改善することがわかります。
まとめ
特徴量ごとに単変量モデルを構築し学習/テストデータでの精度を評価しました。横軸に学習データでの精度、縦軸にテストデータでの精度をplotすると下図になります。
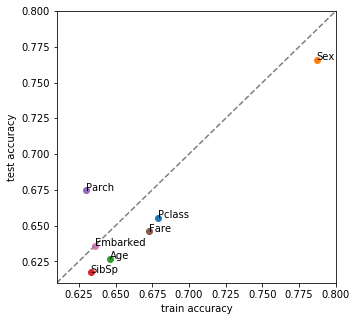
この結果から次のことがわかります。
- 性別モデルが最も良くベースラインモデル編での予想通り[math]75\%[/math]越えの精度を達成
- 乗船港以外はテストデータで精度が変化し生存者の分布が学習データと違う
- 年齢(Age)、SibSpのテストデータでの精度はベースラインモデル以下
特に学習/テストデータで生存者の分布が違うのは厄介な問題で、この後も良いモデルができたと思ってもテストデータだと精度が上がらない現象に悩まされ続けます。
機械学習が学習/テストデータで生存者の分布が同じになることを仮定している以上、特効薬はないのですが
チュートリアルにしては「意地悪な」テストデータになっていること
を知っていればチューニングする際の心理的な大変さが軽減されると思います。