産総研 神嶌先生による転移学習(transfer learning)のサーベイ論文です。人工知能学会 AI書庫にPDFが掲載されています。さらに先生のHP(発表論文)に人工知能学会研究会での発表資料もアップされています。
ここでは論文を
にわけてまとめたいと思います。最近では深層学習を使った画像認識での転移学習(Pre-trained networkやFine tuning)が盛んですがこの論文/発表資料では「機械学習における転移学習」という広い枠組みでサーベイされています。転移学習を広く捉えている分、発表資料によると転移学習の定義すら定まったものがなく転移学習の設定によっては手探りな部分が多いということで先行きに少し不安を覚えました転移学習が成功する理由等がまとめられており参考になります。
転移学習とは
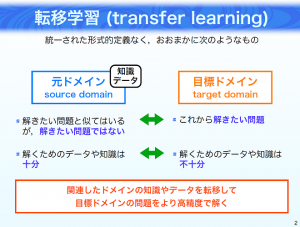
転移学習は幅広い機械学習の枠組みに対して使われている一方で、統一された形式的定義は無いそうです。いきなりおっとっと…という展開ですが、次の定義が広く受け入れられているようです。
新規タスクの効果的な仮説を効率的に見つけ出すために,一つ以上の別のタスクで学習された知識を得て,それを適用する問題
要は「別のタスクで獲得済み知識」を「解きたいタスクに持って行く」ことで解きたいタスクを効率的に解くアプローチと言えます。
(出典:発表資料「転移学習のサーベイ」P.2)
機械学習(特に深層学習)では一般に
- 良質な教師データをいかに多く集められるかが成否を分けるポイント
- 教師データ作成に人手を要することが多く費用、時間の制約がある
という問題がありその解決手段として転移学習が注目されています。
表記
論文で使われている表記についてまとめます。まず、転移する知識の送り手側を元ドメイン(source domain)、受け手側を目標ドメイン(target domain)と呼びそれぞれ上付きの[math]{}^{(S)}, {}^{(T)}[/math]と書き、いずれかのドメインであることを[math]D\in\{S,\ T\}[/math]で示します。
各ドメインの入出力を以下で表記します。
- 入力の定義域:[math]\mathcal{X}^{(D)}[/math]
- 入力:[math]X^{(D)}\in\mathcal{X}^{(D)}[/math]
- 出力の定義域:[math]\mathcal{Y}^{(D)}[/math]
- 出力:[math]Y^{(D)}\in\mathcal{Y}^{(D)}[/math]
例えば0~9が描かれた2値画像の認識が元ドメイン、3桁の数字が書かれたグレースケール画像の認識が目標ドメインの場合、元ドメインの入出力は
- 元ドメインの入力:[math]\mathcal{X}^{(S)}=\{0, 1\}^n[/math]
- 元ドメインの出力:[math]\mathcal{Y}^{(S)}=\{0, 1, \dots,9\}[/math]
- 目標ドメインの入力:[math]\mathcal{X}^{(T)}=\{0, 1,\dots,255\}^m[/math]
- 目標ドメインの出力:[math]\mathcal{Y}^{(T)}=\{000, 001,\dots,999\}[/math]
となります。([math]n, m[/math]は入力画像のサイズ)
転移学習の設定
各ドメインの出力(教師情報)の有無で4つの転移学習の設定が考えられます。本記事では帰納転移学習と呼ばれる「元ドメイン、目標ドメインともに教師情報あり」という最も標準的な設定に絞ってまとめています。
転移過程と転移モデル
元ドメインと目標ドメインがどれだけ「似ているか」が分からないと元ドメインの知識をうまく転移できそうかが分からないのですが、2つのドメインが「似ているか」を定義することは古くから重要な課題として認識されつつも未だに明確な解が示されていないそうです。そこで神嶌先生は
- 転移仮定:どんな観点で類似していてどのように知識を転移できるかを仮定
- 転移モデル:転移仮定を表した数学的モデル
をそれぞれの学習手法で明確にすることを提案されています。
例えば2群判別問題の転移学習において
- 2つのドメインの正例・負例はともに正規分布に従う
- 正例・負例の平均はいずれも元ドメインが目標ドメインの2倍
- 正例・負例の分散はドメイン間で異なる
という状況を仮定できたとするとその仮定を「転移仮定」と呼び、転移仮定にもとづくと元ドメインで得られた判別平面を線形変換することで目標ドメインの判別平面として使えることが分かります。この手続きを数学的に表現したものが「転移モデル」になります。
先生のご提案は現実的な整理法としてとても意義があると思うのですが、実務的には目標ドメインのデータ数が少ないことが多く「転移仮定」の妥当性が検証できないことが多いのが悩ましいですね。
論文では次に転移モデルの分類として「分離アプローチ」と「統合アプローチ」の2つが紹介されています。
分離アプローチ
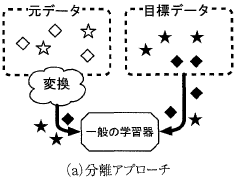
分離アプローチでは元ドメイン側のデータや知識を目標ドメイン側に適合するように変換し、変換したデータを目標ドメインのデータとして扱い一般の学習手法で解きます。学習手法を転移仮定とは独立に選ぶことが出来るのが利点です。
(出典:論文「転移学習」図3(a))
統合アプローチ
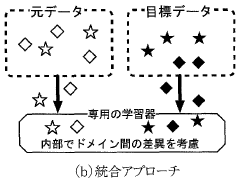
元ドメインのデータは変換せずに目標ドメインに渡しドメイン間の差異に配慮したモデルや手続きで目標ドメインに適した学習結果を得るというアプローチです。転移仮定とモデルを密接に結びつけることが可能になる点が利点です。
(出典:論文「転移学習」図3(b))
転移学習に関連する概念の紹介は以上で、別記事で転移学習手法についてまとめます。




ピンバック: 転移学習 (transfer learning) [深層学習・CNNむけ] | CVMLエキスパートガイド