転移学習（神嶌 敏広 著）：2. 転移学習手法

産総研 神嶌先生による転移学習（transfer learning）のサーベイ論文です。人工知能学会 AI書庫にPDFが掲載されています。さらに先生のHP（発表論文）に人工知能学会研究会での発表資料もアップされています。

論文を以下の2つにわけてまとめており後編にになります。

1. 概念編：論文の1～2章に対応
2. 転移学習手法編：論文の3章に対応（本記事）

なお、帰納転移学習と呼ばれる「元ドメイン、目標ドメインともに教師情報あり」という最も標準的な設定に絞ってまとめています。

転移学習が成功する理由

転移学習全般の議論として大きな影響を与えたThrunの論文とCaruanaの論文が紹介されています。中でもCaruanaの論文では転移学習が成功する理由が考察されており以下の4つになります。

1. データ拡張(data amplification)：共通する因子がある複数タスクがあれば、共通因子のノイズがタスク間でキャンセルされて学習が容易になる
2. 属性選択(attribute selection)：複数タスクを同時に学習させることで、タスク間で共通に有用な特徴の発見がより容易になる
3. 立ち聞き(eavesdropping)：タスク間で難易度で差があれば、容易なタスクから情報を得ることで困難なタスクの学習が容易になる
4. 表現バイアス(representation bias)：各タスクに複数の局所解があれば共通の局所解が選ばれやすくなり他のタスクでは使われない局所解は選ばれにくくなる

ざっくり言うと

ということなんですね。逆に言うと

と言えると思います。

以降、具体的な転移学習方法が紹介されています。なお元ドメイン／目標ドメインの入出力の定義域は等しい、つまり[math]\mathcal{X}^{(S)}=\mathcal{X}^{(T)},\mathcal{Y}^{(S)}=\mathcal{Y}^{(T)}[/math]として話を進めます。

Dauméの「いらいらするほど簡単な方法」

Dauméが提案した「いらいらするほど簡単な方法」^[1]原タイトルは”Frustratingly Easy Domain Adaptation”という面白い名前の方法です。

元ドメインのデータ[math](\mathbf{x}^{(S)}, y^{(S)})[/math]、目標ドメインのデータ[math](\mathbf{x}^{(T)}, y^{(T)})[/math]をそれぞれ

• [math]\left((\mathbf{x}^{(S)}, \mathbf{x}^{(S)}, \mathbf{0}), y^{(S)}\right)[/math]
• [math]\left((\mathbf{x}^{(T)}, \mathbf{0}, \mathbf{x}^{(T)}), y^{(T)}\right)[/math]

に変換して普通の問題として解くだけというシンプルな方法です。両ドメインに共通した特徴については最初の部分が利用され、ドメイン間で働きが異なる特徴については一方のドメインが[math]\mathbf{0}[/math]になっている部分が自然と利用されるという仕組みです。

元ドメイン、目標ドメイン間に比較的シンプルな対応関係が期待できるような状況では学習方法を適切に選べばうまく転移できそうな手法です。

Argyriouのマルチタスク学習

元ドメインのデータのうち目標ドメインでも有用な特徴の部分空間を抽出して、その部分空間に射影した元データを利用する方法がArgyriouによって提案されています。アイディアの骨子は

• マルチタスク学習においてL1正則化項付きのfittingを考える
• L1正則化項によりfittingにあまり寄与しない（≒特定タスクでしか有効でない）特徴の重みは0になる
• 結果的にタスク全体にわたって有用な特徴が選択される

ことが期待でき、得られた特徴の部分空間を目標ドメインへの転移に利用します。

神嶌のTrBagg

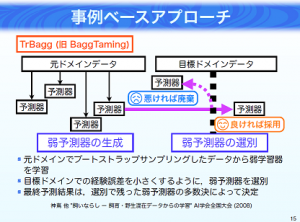
神嶌先生によって別論文で提案されているのがバギングを転移学習に拡張したTrBaggです。弱学習器の生成と選別を行うドメインを使い分けるところがポイントで

• 元ドメインと目標ドメインのデータからBootstrap samplingし弱学習器を生成
• 目標ドメインのデータで弱学習器を選別
• 最終予測は選別した弱学習器の多数決で決定

とします。

（出典：発表資料「転移学習のサーベイ」P.15）

弱学習器には元ドメインのデータが含まれているため目標ドメインに適していない可能性があるため選別は目標ドメインに閉じて行います。

転移学習に関する話題

最後に転移学習の手法そのもの以外で関連する話が紹介されています。

カリキュラム学習

目標タスクを解くための訓練集合を最初から与えるのではなく目標タスクと関連はあるがそれよりも相対的に簡単なタスクを先に学習する手法です。例えば、任意形状の丸、三角、四角の画像を認識するタスクに対して正円、正三角形、正方形だけを含む訓練集合で先に学習する手法です。多峰性の目的関数をオンライン学習する際に

• 良い解に速く収束する
• 汎化性能も改善する

ことが実験的に知られているそうです。機械もいきなり難しい問題を解こうとするのではなく段階的に学習させた方が良いというのは面白いですね。

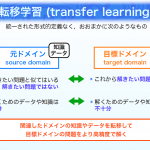
負の転移現象

元ドメインと目標ドメインが大きく異なっていると元ドメインのデータを使ったことでかえって予測精度が落ちる「負の転移現象」（negative transfer）が知られています。わざわざ苦労して元ドメインの知識を取り込もうとしたのに切ない結果になる可能性があるということです。

「負の転移」に対処するために転移学習器の「信頼度」を定義して信頼できそうであればその結果を、信頼できなさそうであれば専門家によるラベル付けを行うような枠組みも提案されているそうです。