2019年11月開催分の解答例です。
例年通りデータの読み取り、確率、確率分布、区間推定、仮説検定、回帰モデルからバランスよく出題されました。過去には難問が混ざることもありましたが今回はオーソドックスな問題が多く解きやすかったと思います。
なお、他の開催分の解答例はこちらを参照ください。
問1
[1]18℃以上が0件、16-18℃が2件なので「1」が適切。
[2]箱の下側が最も高いのは福岡なので「3」が適切。
問2
[3]2015年の図で男性の未婚率はすべて[math]18\%[/math]以上で、女性で[math]18\%[/math]を超えているのは1件のみ。その1件も男性の未婚率の方が高いので「4」が適切。
[4]1990年の図より比較的強い相関があるので[math]r_{1990} > 0.50[/math]と考えられる。2015年の図より1990年と比べ相関は弱くなったと考えられるので「4」が適切。
[5][math]10-12\%[/math]に10件程度あり[math]12-14\%[/math]でピークになるので「3」が適切。
問3
[6]平成31年1月の賃金指数は[math]102.6\times (1-0.0097)[/math]なので平成30年12月からの変化率は「1」が適切。
[7]条件より[math]102.6\times (1+r)^3=105.6[/math]なので「4」が適切。
問4
[8]各記述は
- 必ずしも直線で表せるとは限らないため「誤」
- 季節変動は年周期変動を表すので「正」
- 不規則変動には偶然変動も含めるので「誤」
より「2」が適切。
問5
[9]12か月周期があり6か月前とは負の相関があると考えられるので「2」が適切。
問6
[10]それぞれ単純無作為抽出、層化抽出、集落抽出を表すので「4」が適切。
問7
[11]標準誤差は[math]\frac{\hat{\sigma}}{\sqrt{n}}=\frac{\sqrt{16.0}}{\sqrt{100}}=0.40[/math]より「3」が適切。
問8
[12]試験に合格した事象を[math]S[/math], 対策講座の受講した事象を[math]A[/math]とすると
[math]
\begin{eqnarray}
P(A \cap S) &=& P(A)P(S|A) \\
&=& 0.20 \times 0.70 \\
&=& 0.14
\end{eqnarray}
[/math]
より「1」が適切。
[13]まず[math]P(S)=P(A)P(S|A)+P(\bar{A})P(S|\bar{A})=0.38[/math]なので
[math]
\begin{eqnarray}
P(A|S) &=& \dfrac{P(A \cap S)}{P(S)} \\
&=& \dfrac{0.14}{0.38}\\
&=& 0.368
\end{eqnarray}
[/math]
より「3」が適切。
問9
[14][math]\int f(x)dx = 1[/math]より[math]a=\frac{1}{10}[/math]なので「4」が適切。
[15][math]E[X]=\int xf(x)dx=\frac{20}{3}[/math]より「4」が適切。
[16][math]X < 10[/math], [math]10 \leq X < 15[/math], [math]X \geq 15[/math]となる確率を求め期待値を求めると1,040円となり「2」が適切。
問10
[17]確率変数[math]Z[/math]と[math]X[/math]の関係を図示すると
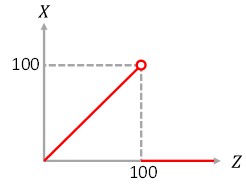
になる。これより[math]0 \leq x < 100[/math]に対し
[math]
\begin{eqnarray}
F_X(x) &=& P(X \leq x) \\
&=& P(Z \leq x) + P(Z > 100) \\
&=& F_Z(x) + 0.04
\end{eqnarray}
[/math]
より「3」が適切。
[18][math]F_X(5)=F_Z(5)+0.04=0.95[/math]より「2」が適切。
[19][math]E[X]=\int_0^{100} x F’_X(x)dx=\int_0^{100} zf_Z(z)dz[/math]より「2」が適切。
問11
[20]歪度は[math]\frac{E[(X-\mu)^3]}{\sigma^3}[/math]で与えられるので各記述は
- 分布の平均の正負と歪度の正負は関係なく「誤」
- 右に裾の長い分布の歪度は正になるので「誤」
- 多峰性と歪度の正負は関係なく「誤」
より「5」が適切。
問12
[21][math]\hat{\mu}_1 \sim \mathcal{N}(\mu, \sigma^2/2)[/math], [math]\hat{\mu}_2 \sim \mathcal{N}(\mu, \sigma^2/n)[/math]なので
- [math]\hat{\mu}_1[/math]: 不偏推定量だが一致推定量ではない
- [math]\hat{\mu}_2[/math]: 不偏推定量であり一致推定量でもある
ので「5」が適切。
問13
[22]母比率の信頼区間は
[math]
\hat{p} – z_{\alpha/2}\sqrt{\frac{
\hat{p}(1-
\hat{p})}{n}} \leq p \leq \hat{p} + z_{\alpha/2}\sqrt{\frac{
\hat{p}(1-
\hat{p})}{n}}
[/math]
で与えられる。[math] \hat{p}=0.54, z_{\alpha/2}=1.96, n=100[/math]より[math]95\%[/math]信頼区間は[math]0.54\pm 0.098[/math]となり「5」が適切。
問14
[23]中央値は「400万円以上500万円未満」の階級に含まれる。中央値の半分は「200万円以上250万円未満」なので世帯割合は[math]19.6\%[/math]以上[math]33.3\%[/math]以下になり「3」が適切。
[24]統計量[math]Z[/math]は[math]t[/math]分布に従い[math]n[/math]が十分大きいと標準正規分布で近似でき「3」が適切。
問15
[25]母比率の信頼区間幅は
[math]
2z_{\alpha/2}\sqrt{\dfrac{
\hat{p}(1-
\hat{p})}{n}}
[/math]
で与えられる。信頼区間幅を[math]6\%[/math]以下にするには
[math]
\begin{eqnarray}
&& 2z_{\alpha/2}\sqrt{\frac{
\hat{p}(1-
\hat{p})}{n}} \leq 0.06 \\
&\Leftrightarrow& n \geq \hat{p}(1-\hat{p})\left(\frac{1.96}{0.03}\right)^2
\end{eqnarray}
[/math]
となるように[math]n[/math]を決めればよい。支持率について情報がない場合は[math]0 \leq \hat{p} \leq 1[/math]での右辺の最大値を考えて[math]n \geq 1067[/math]であればよい。よって「4」が適切。
[26][math]\hat{p}=0.80[/math]とすると[math]n \geq 682[/math]となるので「2」が適切。
問16
[27]自由度[math]16-1=15[/math]の[math]t[/math]分布に従うので「5」が適切。
[28]体重の減少([math]\mu > 0[/math])を検証したいので帰無仮説[math]\mu=0[/math], 対立仮説[math]\mu > 0[/math]とする「4」が適切。
[29][math]t=1.33 < 1.75[/math]となり帰無仮説は棄却できず摂取後に体重が減少するとは言えず「5」が適切。
問17
[30]水準間平方和は「水準平均と全体平均の平方和」、残差平方和は「各データと水準平均の平方和」なので「1」が適切。
[31]水準間の自由度[math]F_1[/math]は水準数-1、残差平方和の自由度は[math]12\times 11 – F_1=120[/math]なので「3」が適切。
[32]各記述は
- 一元配置分散分析の対立仮説は[math]\mu_i[/math]いずれかが異なるなので「誤」
- 検定を行うと有意差があるため「誤」
- 検定を行うと有意差があり「正」
より「3」が適切。
問18
[33]各説明変数を1単位だけ増やすと目的変数は回帰係数の値分だけ変動する。これより「1」が適切。
[34]
各記述は
- 予測値の平均は元データの平均に一致するので「正」
- 予測値の平均=[math]\hat{\beta}_0+\hat{\beta}_1\times[/math](世帯収入合計の平均)が成立するので「正」
- 元データと予測値の差が残差のため「正」
より「5」が適切。
[35]各記述は
- 重回帰モデルで係数を等しいと置くと定期収入と賞与の和を考えたモデルになり単回帰モデルが得られ「正」
- 統計ソフトウェアの出力結果からは重回帰モデルの自由度調整済み決定係数の方が小さいので「誤」
- 分析できる関係性を正しく説明しており「正」
より「3」が適切。