教師あり学習の最も基本的な手法として単回帰の考え方と基本的な性質として
- 回帰係数の導出
- 回帰直線の性質
- 計算量
を紹介します。
単回帰
単回帰は[math]N[/math]個の
- 説明変数: [math]x_i\in \mathbb{R}[/math]
- 目的変数: [math]y_i\in \mathbb{R}[/math]
の組[math](x_i, y_i),\ i=1,2,\dots,N[/math]から説明変数と目的変数間の関係
[math]
y = \beta_0 + \beta_1 x,\quad \beta_0, \beta_1\in \mathbb{R}
[/math]
を求める手法です。この直線を回帰直線と呼びます。説明変数[math]x[/math]が1単位を大きくなると目的変数[math]y[/math]が[math]\beta_1[/math]だけ大きくなることを表しており解釈しやすいモデルです。
以下で見るようにデータさえあれば回帰直線を求めることができますが、単回帰は説明変数と目的変数間に比例関係を仮定しており学習データで本当に比例関係があるのか可視化して確認しておく必要があります。
回帰係数の導出
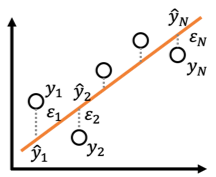
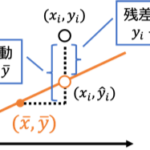
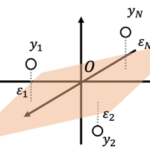
線形回帰では回帰係数[math](\beta_0,\beta_1)[/math]を動かすと回帰直線の傾き、切片を動かすことができます。回帰直線の良し悪しを予測値[math]\hat{y}_i=\beta_0 + \beta_1 x_i[/math]と目的変数[math]y_i[/math]の差[math]
\varepsilon_i= y_i – \hat{y}_i[/math]の二乗和
[math]
\begin{eqnarray}
L(\beta_0, \beta_1) &=& \sum_{i=1}^N \varepsilon_i^2 \\
&=& \sum_{i=1}^N \left( y_i – (\beta_0 + \beta_1 x_i) \right)^2
\end{eqnarray}
[/math]
で表現し、[math]L(\beta_0, \beta_1)[/math]を最小化する直線を求めます。モデルのパラメタを決定するために用いる関数[math]L[/math]を損失関数(Loss function)と呼びます。線形回帰では回帰係数[math](\beta_0,\beta_1)[/math]を解析的に求めることができます。
[math]
\begin{eqnarray}
\hat{\beta}_0 &=& \bar{y} – \
\hat{\beta}_1\bar{x} \\
\hat{\beta}_1 &=& \dfrac{S_{xy}}{S_{xx}}
\end{eqnarray}
[/math]
で与えられる。ここで[math]\bar{x}=\frac{1}{N}\sum_{i}x_i[/math], [math]\bar{y}=\frac{1}{N}\sum_{i}y_i[/math], [math]S_{xx} = \sum_i (x_i – \bar{x})^2[/math], [math]S_{xy} = \sum_i (x_i – \bar{x})(y_i – \bar{y})[/math]である。
[math]L(\beta_0, \beta_1)[/math]は[math]\beta_0, \beta_1[/math]の2次関数なので
[math]
\begin{eqnarray}
\dfrac{\partial L}{\partial \beta_0} &=& -2\sum_{i=1}^N \left(y_i – \beta_0 – \beta_1 x_i \right) = 0 \\
\dfrac{\partial L}{\partial \beta_1} &=& -2\sum_{i=1}^N x_i\left(y_i – \beta_0 – \beta_1 x_i \right) = 0
\end{eqnarray}
[/math]
を解けばよいです。第一式を式変形すると
[math]
\hat{\beta}_0 = \bar{y} – \
\hat{\beta}_1\bar{x}
[/math]
が得られます。この結果を用いて第二式を整理すると
[math]
\begin{eqnarray}
&& N\bar{x}\hat{\beta}_0 + \hat{\beta}_1\sum_{i=1}^N x_i^2 – \sum_{i=1}^N x_iy_i = 0 \\
&\Leftrightarrow& \hat{\beta}_1\left(\sum_{i=1}^N x_i^2 – N\bar{x}^2 \right) – \left(\sum_{i=1}^N x_iy_i – N\bar{x}\bar{y}\right) = 0 \\
&\Leftrightarrow& \hat{\beta}_1S_{xx} – S_{xy} = 0
\end{eqnarray}
[/math]
となり[math]x_1=x_2=\cdots=x_N[/math]でないことより[math]S_{xx} \ne 0[/math]なので[math]\hat{\beta}_1 = \dfrac{S_{xy}}{S_{xx}}[/math]が得られます。
回帰直線の性質
回帰直線は
[math]
\begin{eqnarray}
y &=& \hat{\beta}_0 + \hat{\beta}_1 x \\
&=& \bar{y} + \hat{\beta}_1(x – \bar{x})
\end{eqnarray}
[/math]
と書けるので点[math](\bar{x}, \bar{y})[/math]を通ることがわかります。まとめると以下になります。
ハイパーパラメタ
単回帰は学習アルゴリズムの挙動を制御するハイパーパラメタはなくパラメタチューニングは不要です。
計算量
単回帰の回帰係数は[math]x_i[/math]の平均[math]\bar{x}[/math], [math]y_i[/math]の平均[math]\bar{y}[/math]および[math]S_{xx} = \sum_i (x_i – \bar{x})^2[/math], [math]S_{xy} = \sum_i (x_i – \bar{x})(y_i – \bar{y})[/math]を計算すれば良いのでそれぞれ[math]O(N)[/math]の計算量で計算できます。
予測時は[math]\hat{\beta}_0 + \hat{\beta}_1 x[/math]を計算するだけなので[math]O(1)[/math]で計算できます。まとめると
- 学習: [math]O(N)[/math]
- 予測: [math]O(1)[/math]
でモデルの学習および予測ができる。
データ数[math]N[/math]に比例した計算量で学習し、定数時間で予測できる非常に高速な手法です。
シリーズ記事
「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「単回帰」の性質を紹介しています。
誤差項について「無相関で分散一定」「独立同一な正規分布」を仮定するとで様々な性質を導くことができますが、ここでは誤差項について特に仮定せずに導ける性質として
- 考え方と基本的な性質(本記事): 回帰係数の導出、回帰直線の性質、計算量との関係
- 決定係数: 決定係数と相関係数の関係
- 予測の留意点: 学習データ外の値や外れ値で予測する場合の留意点と対処法
- 外れ値の影響: 外れ値が学習時に与える影響
を解説しています。
また単回帰を拡張した「重回帰」でも同様の性質を示せるのでそちらも参照ください。