単回帰モデルと決定係数の関係

「単回帰の考え方と基本的な性質」に続き学習データへの当てはまりの良さを表す「決定係数」を紹介し、単回帰モデルでの決定係数と相関係数の関係を導きます。

決定係数

決定係数（coefficient of determination）とは機械学習モデルが学習データにどれだけ当てはまっているかを評価する指標です。

• 学習データ: [math](x_i, y_i),\ i=1,2,\dots,N[/math]
• モデルの予測値: [math]\hat{y}_i,\ i=1,2,\dots,N[/math]

として決定係数[math]D[/math]は

[math]

\displaystyle D := 1 – \dfrac{\sum_{i=1}^N (y_i – \hat{y}_i)^2}{\sum_{i=1}^N (y_i – \bar{y})^2}
[/math]

で与えられます。ここで[math]\bar{y}=\frac{1}{N}\sum_{i}y_i[/math]です。

決定係数の意味ですが

[math]i[/math]番目のデータ[math](x_i, y_i)[/math]およびその予測値[math](x_i, \hat{y}_i)[/math]に着目します。

• 全変動: [math]y_i[/math]と平均[math]\bar{y}[/math]との差
• 残差変動: [math]y_i[/math]と予測値[math]\hat{y}_i[/math]との差

と呼びます。決定係数は「全変動の平方和」に対する「残差変動の平方和」の割合を1から引いた値になります。予測値が学習データに近い、つまりモデルが学習データによく当てはまっている場合に決定係数は1に近くなります。

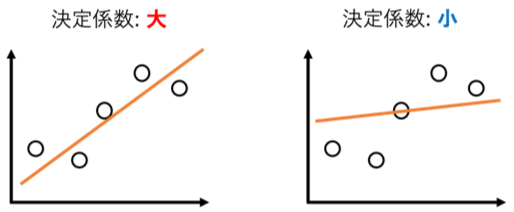
決定係数の性質

決定係数の性質として以下を示すことができます。

1. 定義より自明です。
2. [math]D=1[/math]と「残差変動の平方和が0」つまり「[math]\hat{y}_i=y_i[/math]」と同値のため成立します。
3. 平均値で予測するモデル（上の図で回帰直線が[math]y=\bar{y}[/math]の場合）の「残差変動」は「全変動」と一致するので[math]D=0[/math]になります。
4. ある予測値[math]\hat{y}_i[/math]を[math]\hat{y}_i\to\infty[/math]とすると[math]D\to -\infty[/math]なので十分大きな[math]\hat{y}_i[/math]があると[math]D[/math]は負の値をとることがあります。

性質1〜3から「平均値で予測するモデル」や「完全に学習データを説明できるモデル」と比べモデルがどれくらい学習データを当てはめられているかを評価できます。

モデルの評価指標としてよく使われますが、この記事で紹介したように外れ値があると当てはまっていないように見えるモデルでも決定係数が高くなるため鵜呑みにせず当てはまり結果を可視化して確認することをオススメします。

また、決定係数を表す文字としてよく[math]R^2[/math]が用いられ決定係数が常に0以上の値をとるように見えますが、性質4から一般のモデルに対しては負の値をとることがあります。

単回帰モデルでの決定係数と相関係数の関係

ここからはモデルが単回帰の場合を考えます。つまり

[math]


y = 
\hat{\beta}_0 + 
\hat{\beta}_1 x
[/math]

で予測するモデルを考えます。ただし、[math]\hat{\beta}_0 = \bar{y}-\hat{\beta}_1\bar{x}[/math]
, 
[math]\hat{\beta}_1 = \dfrac{S_{xy}}{S_{xx}}[/math]で

• [math]\bar{x}=\frac{1}{N}\sum_{i}x_i[/math]
• [math]\bar{y}=\frac{1}{N}\sum_{i}y_i[/math]
• [math]S_{xx} = \sum_i (x_i – \bar{x})^2[/math]
• [math]S_{yy} = \sum_i (y_i – \bar{y})^2[/math]
• [math]S_{xy} = \sum_i (x_i – \bar{x})(y_i – \bar{y})[/math]

です。

この時、出力データ[math]y_i[/math]と入力データの予測値[math]\hat{y}_i[/math]の相関係数[math]\rho[/math]

[math]
\rho = \dfrac{\sum_i \left(y_i – \bar{y}\right)\left(\hat{y}_i – \bar{\hat{y}}\right)}{\sqrt{\sum_i \left(y_i-\bar{y}\right)^2} \sqrt{\sum_i \left(\hat{y}_i-\bar{\hat{y}}\right)^2} }
[/math]

と決定係数[math]D[/math]には次の関係が成立します。

単回帰モデルの予測値について成立する以下の性質を組合せて示します。

1. [math]\rho^2[/math]と[math]S_{xx},\ S_{yy},\ S_{xy}[/math]の関係
2. 全変動の平方和[math]S_{yy}[/math]の分解
3. 決定係数[math]D[/math]と[math]\rho^2[/math]の関係

[math]\rho^2[/math]と[math]S_{xx},\ S_{yy},\ S_{xy}[/math]の関係

まず、単回帰モデルの基本的な性質で触れたように予測値の平均[math]\bar{\hat{y}}[/math]は目的変数の平均[math]\bar{y}[/math]と一致します。これより

[math]
\begin{eqnarray}
\hat{y}_i – \bar{\hat{y}} &=& 
\hat{y}_i – \bar{y} \\
&=& \hat{\beta}_1(x_i – \bar{x})
\end{eqnarray}
[/math]

と書けることに注意すると[math]\rho^2[/math]は

[math]
\begin{eqnarray}

\rho^2 &=& \dfrac{\left\{\sum_i \left(y_i – \bar{y}\right)\left(\hat{y}_i – \bar{\hat{y}}\right)\right\}^2}{\sum_i \left(y_i-\bar{y}\right)^2 \sum_i \left(\hat{y}_i-\bar{\hat{y}}\right)^2 } \\
&=& \dfrac{\hat{\beta}_1^2 \left\{\sum_i \left(y_i – \bar{y}\right)(x_i – \bar{x}) \right\}^2 }{S_{yy}\cdot \hat{\beta}_1^2 \sum_i \left(x_i-\bar{x}\right)^2} \\
&=& \dfrac{S_{xy}^2}{S_{xx}S_{yy}}
\end{eqnarray}
[/math]

と書けます。

全変動の平方和[math]S_{yy}[/math]の分解

次に決定係数[math]D[/math]を整理していきます。まず次の補題を示します。

第三項の[math]\hat{y}_i – \bar{\hat{y}}[/math]を回帰変動と呼びます。この補題は単回帰モデルでは

「全変動の平方和[math]S_{yy}[/math]」を「残差変動の平方和[math]S_e[/math]」と「回帰変動の平方和[math]S_{\hat{y}\hat{y}}[/math]」に分解

できることを示しています。

証明は全変動を[math]y_i – \bar{y} = y_i – \hat{y}_i + (\hat{y}_i – \bar{\hat{y}})[/math]とみると

[math]
\begin{eqnarray}

&& \sum_{i=1}^N (y_i – \bar{y})^2 \\
&=& S_e + 2\sum_{i=1}^N (y_i – \hat{y}_i)(\hat{y}_i – \bar{\hat{y}}) + S_{\hat{y}\hat{y}}
\end{eqnarray}
[/math]

となります。第二項は[math]\hat{y}_i = \bar{y} + \hat{\beta}_1(x_i – \bar{x})[/math]および[math]\hat{\beta}_1 = \dfrac{S_{xy}}{S_{xx}}[/math]より

[math]
\begin{eqnarray}

&& \sum_{i=1}^N \left(y_i – \hat{y}_i\right)\left(\hat{y}_i – \bar{\hat{y}}\right) \\
&=& \sum_{i=1}^N \left(y_i – \bar{y} + \hat{\beta}_1(x_i – \bar{x})\right)\cdot \hat{\beta}_1(x_i – \bar{x}) \\
&=& \hat{\beta}_1 S_{xy} – \hat{\beta}_1^2S_{xx} \\
&=& \dfrac{S_{xy}}{S_{xx}}S_{xy} – \dfrac{S_{xy}^2}{S_{xx}^2}S_{xx} \\
&=& 0
\end{eqnarray}
[/math]

と消えるので補題が成立します。

決定係数[math]D[/math]と[math]\rho^2[/math]の関係

それでは決定係数[math]D=1-\dfrac{S_e}{S_{yy}}[/math]を整理していきましょう。[math]S_{yy} = S_e + S_{\hat{y}\hat{y}}[/math]なので

[math]
\begin{eqnarray}

D &=& 1 – \dfrac{S_e}{S_{yy}} \\
&=& \dfrac{S_{yy}-S_e}{S_{yy}} \\
&=& \dfrac{S_{\hat{y}\hat{y}}}{S_{yy}}
\end{eqnarray}
[/math]

と変形でき[math]\hat{y}_i – \bar{y} = \hat{\beta}_1(x_i – \bar{x})[/math]より[math]S_{\hat{y}\hat{y}}=\hat{\beta}_1^2S_{xx}[/math]なので

[math]
\begin{eqnarray}

&=& \hat{\beta}_1^2\dfrac{S_{xx}}{S_{yy}} \\
&=& \dfrac{S_{xy}^2}{S_{xx}^2}\dfrac{S_{xx}}{S_{yy}} \\
&=& \dfrac{S_{xy}^2}{S_{xx}S_{yy}} \\
&=& \rho^2
\end{eqnarray}
[/math]

が成立します。

この結果から単回帰の決定係数は[math]D=\rho^2 \geq 0[/math]が保証され「平均値で予測するモデル」と比べ（決定係数の意味で）当てはまりの良いモデルと言えます。

シリーズ記事

「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「単回帰」の性質を紹介しています。

誤差項について「無相関で分散一定」「独立同一な正規分布」を仮定するとで様々な性質を導くことができますが、ここでは誤差項について特に仮定せずに導ける性質として

• 考え方と基本的な性質: 回帰係数の導出、回帰直線の性質、計算量との関係
• 決定係数（本記事）: 決定係数と相関係数の関係
• 予測の留意点: 学習データ外の値や外れ値で予測する場合の留意点と対処法
• 外れ値の影響: 外れ値が学習時に与える影響

を解説しています。

また単回帰を拡張した「重回帰」でも同様の性質を示せるのでそちらも参照ください。