今週のまとめ
- ABC 220, 219のバチャやった
- 新しいPCを注文した
- 恐竜ラボ!ディノサバイバルに行った
- ABC286に出た。冷えた
です。
(本文中にABC 051 D, 219 C-F, 220 B,E,F, 243 E, 286 A-Fの解法を含む話題が出てくるのでご注意ください。)
1/15(Sun)
先週の週記で書いた通りABC285に出てました。
来週1/23-25で出張するのでホテルの予約。今の会社は出張のルールが柔軟でとてもやりやすい。出張先からすぐ近くのホテルを予約しました。健全。
1/16(Mon)
今の会社は「朝当番」というのがあって朝一で出社して庶務の方が出社するまで問合せ対応。昨日はABC直後のせいか寝つきが悪く朝は正直眠い。
天下一品もいつの間にか値上がりして基本的に1000円オーバーですねぇ。梅田だとランチは1000円前後が相場になってきた感じです。
1/17(Tue)
ABC220のバーチャル参加
5完1ペナでパフォーマンス1343相当。
「B – Base K」はK進数、10進数がこんがらがってサンプルを合わせるのにも苦労。出すとなんとWA。原因が分からずしばし苦悶。
原因はオーバーフロー。A,Bが[math]10^5[/math]付近だと2進数表記すると17桁になる。long longだと大丈夫ですが途中の処理をintしていたのが原因。
基数が小さいと桁数が大きくなるので文字列で受け取るのが安全ですね。
「E – Distance on Large Perfect Binary Tree」は木の深さごとに足しあげていく。いったん、愚直解[math]O(N^2)[/math]で答えを合わせてから累積和で[math]O(N)[/math]にしました。コーナーケースに気づけたのでこの動きは良かった。
バチャ中はここまで。
「F – Distance Sums 2」は木の各ノードから見た距離の総和を求める問題。最初、嘘のDPを書いてしまってサンプルすら合わず。冷静に考えると
- 根を適当に決め各ノードの部分木のサイズを求めておく
- ある頂点からの距離の総和を求めておく
- ノードAからノードBに移ると距離の総和はAの部分木のノード数分増えて、Bの部分木のノード数分減る
と差分を[math]O(1)[/math]で出せ全体を[math]O(N)[/math]で出せます。水Diff前半なので有名問題なのかも。
1/18(Wed)
ABC 051「D – Candidates of No Shortest Paths」を解いてみたが、1時間内に解けず。
原因は問題の誤解。「どの最短経路にも含まれない辺の個数」を求めるのを「辺を除いても頂点間の最短距離が変わらない」と思って解いてました。
前者の方が簡単で辺[math](i, j)[/math]の重みが[math](i, j)[/math]の最短距離より真に小さい場合を考えればOK。
最短距離に関連する考察は
- [math]d(i, j)[/math]: ノード[math](i, j)[/math]間の最短距離
- [math]e(i, j)[/math]: 辺[math](i, j)[/math]間の重み
として各ノードペア[math](s, j)[/math]で
[math]d(s, j) = \min\left\{d(s, i) + e(i, j)\ |\ (i, j) \in E\right\}[/math]
辺[math](i, j)[/math]が最短路になる必要十分条件はある[math]s[/math]が存在して
[math]d(s, j) = d(s, i) + e(i, j)[/math]
となることです。どの最短路にもならないのはすべての[math]s[/math]について上式が成り立たない時になります。[math]s=i[/math]でも成立しないので[math]d(i, j)>e(i,j)[/math]が分かり、逆にこの時は上式が成立しないので[math]d(i, j)>e(i,j)[/math]を満たす辺を数えれば良いことが分かります。
類題としてABC 243「E – Edge Deletion」がありこちらは「辺を除いても頂点間の最短距離が変わらないもの」を数える問題ですが同様の考察ができます。
1/19(Thr)
ABC219のバーチャル参加
4完でパフォーマンス1543相当。水Diff前半まではスムーズに解けパフォーマンスの下限は安定してますが、水Diff後半以降が解けないことも多く上限も伸び悩んでますね。
「C – Neo-lexicographic Ordering」は各名前をa-z順に戻した時とのpairで持ちsortして出力。
「D – Strange Lunchbox」はいかにもDP。i個目まで見てたこ焼きx個、たい焼きy個を食べるために必要な最小個数としてDPを構成すればOK。
バチャ中はここまで。Eをしばらく考えて経路を全探索したらTLEするのでは?という疑問が解消しなかったのと内部判定の良い方法が思いつかなったのでFへ行ってそれっぽい考察にたどり着いて実装しているうちに終了。
「F – Cleaning Robot」はメモを書いていたら長くなったので別記事に。これ橙Diffなんですね。ヒントなしで自力で通したのはABC225「F – String Cards」以来2問目。
1/20(Fri)
ABC219「E – Moat」をupsolve。4×4のセルのうちいくつかのセルが指定されておりそれらをすべて含む囲い方を求める問題。
囲む経路の全探索ではなく内部とするセルを全探索すれば内部のセルは16個しかないので十分高速です。
あとは内部と決めたセルが自己交差しないように辺をつないで閉路にできるか?ですが
- 隣接する内部同士/外部同士を連結する
- 内部の連結成分が一つであること
- 外部の連結成分がセルの外周と接していること
をチェックすれば良いです。最後の条件は内部の連結成分がドーナツ型になるのを除くためです。
連結成分の座標の最大/最小でチェックしましたが解説動画によると1周分余分にとった6×6のセルで考えて最外周を外部とすると「連結成分が2つ」で判定できました。
さらに経路の探索でもできたみたいです。経路数が多くてTLEを心配しましたが2点A, BをきめてA→B→Aと戻る経路は高々[math]{}_8C_4^2[/math]通りくらいなので全部試しても[math]{}_5C_2\cdot{}_8C_4^2=4.9\times 10^4[/math]くらいでそれほど多くないですね。
面白いのが内部判定の方法。どうやるんだろう?と思いましたが
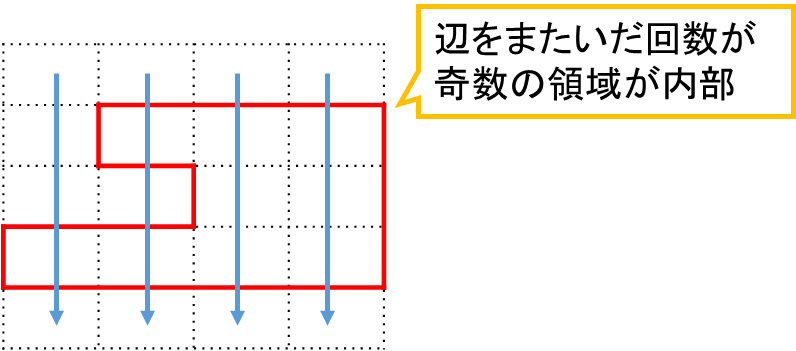
方向を適当に一つ決めて(図だと上から下)「辺をまたいだ回数が奇数回だと内部」になります。これは言われてみるとなるほどーという判定方法。
PCの買い替え
メインPCを10年以上使ってて突然落ちることが増えたので買い替えることにしました。
せっかくなので競プロライフが幸せになるように…と思いましたがアルゴはシングルスレッド性能とストレージ性能であまり劇的な変化はなさそう[1]さすがに10年経つと違うか?。
ヒューリスティックコンはテストを並列化して時間短縮するというのが常套手段なのでコア/スレッド数の多いCPUがいいですね。
最新CPUだとインテルは高性能コアと高効率コアを分けているようで並列化した時にどっちに割当たるかで性能が変わりそうで微妙な感じ。AMDだと同質コアで構成されておりこの心配はなさそうです。そうなると手を出せるのは16コア32スレッドのRyzen 9 7950Xが上限[2]Threadripperという64コア/128スレッドCPUがありますが100万くらいする。。CPUだけで10万円近いのでかなりいいお値段。この瞬間だけ円高にならないかな…。
みたいなことを昨年末から考えていたら1/20になってこの日に注文。もともと次のAHCで使おうと思って考え始めたのですがAHC017の終盤に届くことになりそう。
Linus Torvalds「ギリギリになってあわてて作業するのは高校で卒業すべき[3]https://gigazine.net/news/20221019-linus-tovalds-say-stop-pull-all-nighters/」
ギリギリどころか1週間遅かったです。はい。
1/21(Sat)
家族で「恐竜ラボ!ディノサバイバル」を見に行きました。

どういうものかよくわからずに付いて行ったのですが「学ぶ!体感!」「迫力の舞台!」で恐竜が出てくる公演のようです。前説的な話が終わり恐竜を呼び出すのですが

めっちゃリアル!です。のしのし動き回って迫力抜群。すげー。途中、途中でクイズとかあって教育的要素もありますが恐竜がリアル過ぎて頭に入ってきません…というくらいリアルで大人でも楽しめました。
ABC286の参加
5完(1ペナ、53分)、パフォーマンス1414でレートは1539(-13)へ。ここでも易しめの問題は解けるが水Diff後半以降が間に合わない…という流れになってしまいました。
Fは正しい考察はできたのに手元でデバッグせず提出デバッグという雑なことをして2分間に合わないというもったいないことに。まぁ自業自得です。
「A – Range Swap」はインデックスや区間を取り違えて10分かけてようやく通る。素直に[P,Q], [R,S]をswapした方が良かった。
「B – Cat」は2文字ずつ見ていってnyならnya, それ以外はそのまま出力。
「C – Rotate and Palindrome」はある文字列を回文にする必要な回数は前後i番目が異なる文字の数になります。あとは[math]O(N^2)[/math]が間に合うので[math]N[/math]通りのシフト文字列についてコストを出して最小を求めればOK。
「D – Money in Hand」は個数制限付き部分和問題。愚直でも間に合いそうでしたが念のため[math]O(NX)[/math]で書きました。これ茶Diffなんですね。レベル高い。
「E – Souvenir」は最初、最短路のBFSが[math]O(V)[/math]と勘違いしてクエリごとに実行してしまいTLE。事前に全点最短路を求めておきクエリごとにs, t間の最短経路のなかで価値最大のものをdfsで求めました。
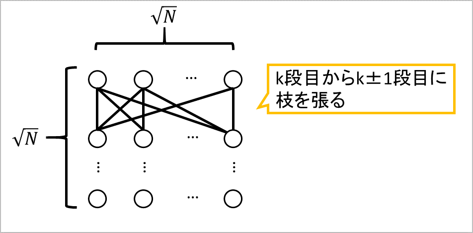
Eの解法について(2023/01/26追記)
提出した解法は本来TLEするものでした。
上記のようなグラフで最上段から最下段への経路で価値最大をdfsで求めると[math]O(N\sqrt N)[/math]かかりTLEします。(2ノード間の最大価値をメモ化しておくと大丈夫です。)
Twitterで指摘いただきました。この場を借りて感謝します。
(追記ここまで)
「F – Guess The Number 2」は長さ[math]p[/math]の巡回列にして渡すと数列[math]B[/math]で巡回列の先頭の数字がどこにあるかで[math]N[/math]を[math]p[/math]で割った余りが分かります。
[math]p[/math]を複数用意して余りから[math]N[/math]を復元します。[math]\{p_i\}[/math]で和が[math]110[/math]以下、積が[math]10^9[/math]となるものを探します。最初、素数で探すと微妙にオーバー。確か互いに素なら復元できたんじゃないか?と記憶を思い起こし実験して確認。いけそうなので互いに素で探します。

見つかりました。おっしゃ、これはもらった!と実装しますが数列の要素が108個になりジャッジ側を手でやるのが辛くエイやと出してはTLE, WAを食らうという提出デバッグをしているうちに終了。2分差で間に合わず(涙)
あああぁ…Fが2分間に合わず…(涙) pic.twitter.com/YCobti81no
— starpentagon (@stat_learning) January 21, 2023
ちゃんとジャッジ側も書いてテストできるようにします。あと互いに素な数で割った余りから元の数を求めるのは中国剰余定理ですね。高校の時にやった記憶がありますがほぼ忘れているのでまた学びます。
来週の土曜からAHC017ですね。楽しみです。こちらに参加中はABCはお休み予定です。
関連記事
- 前週の週記: 「イルミネーションを見ながらLISの復元に思いをはせる」
- 翌週の週記: 「久しぶりに東京へ」
脚注
| ↑1 | さすがに10年経つと違うか? |
|---|---|
| ↑2 | Threadripperという64コア/128スレッドCPUがありますが100万くらいする。 |
| ↑3 | https://gigazine.net/news/20221019-linus-tovalds-say-stop-pull-all-nighters/ |







ピンバック: 週記(23/01/08週):イルミネーションを見ながらLISの復元に思いをはせる | 有意に無意味な話
ピンバック: 週記(23/01/22週):久しぶりに東京へ | 有意に無意味な話