正規母集団（分散既知）の平均に関する検定

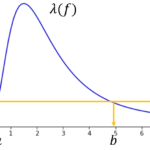
汎用的な検定方法として尤度比

[math]
\lambda(\mathbf{x}) = \dfrac{\sup_{\theta\in\Theta_0}L(\theta\ |\ \mathbf{x})}{\sup_{\theta\in\Theta}L(\theta\ |\ \mathbf{x})}
[/math]

を使った「尤度比検定」を紹介しました。

ここでは

母集団が正規分布[math]\mathcal{N}(\mu, \sigma^2)[/math]に従う
分散[math]\sigma^2[/math]が既知

の場合に平均[math]\mu[/math]に関する尤度比検定は「標準正規分布を使った検定」に帰着できることを示します。

問題設定

母集団が正規分布に従い、その分散は[math]\sigma^2=100[/math]など具体的に値が分かっているものとします。分散が既知であることを明確にするために[math]\sigma^2=\sigma_0^2[/math]（[math]\sigma_0^2[/math]は既知の定数）と表記します。

この母集団から無作為抽出した標本を[math]X_i(i=1,\dots,n)[/math]として平均[math]\mu[/math]に関する次の両側検定を考えます。

[math]H_0[/math]: [math]\mu=\mu_0[/math]
[math]H_1[/math]: [math]\mu\ne\mu_0[/math]

数式だけだとイメージしにくいので次の例題を考えてみます。

小学校1年生（男子）全体の身長は平均119.6cm, 標準偏差が5.1cmである正規分布であった。ある地域で小学校1年生（男子）を100名を無作為に選び平均を求めると121.2cmであった。この地域の平均身長[math]\mu[/math]は全国平均とは異なると言って良いだろうか？

この地域の小学校1年生（男子）の身長は[math]\mathcal{N}(\mu,5.1^2)[/math]に従うと考えられ

[math]H_0[/math]: [math]\mu=119.6[/math]（この地域の平均は全国平均と同じ）
[math]H_1[/math]: [math]\mu\ne 119.6[/math]（この地域の平均は全国平均とは異なる）

を適当な有意水準の下で検定することで平均が異なっていそうか判断できます。

尤度比検定

まず、正規分布[math]\mathcal{N}(\mu, \sigma_0^2)[/math]の確率密度関数[math]f(x|\mu)[/math]は

[math]
f(x|\mu)=\dfrac{1}{\sqrt{2\pi\sigma_0^2}}\exp\left[-\frac{(x-\mu)^2}{2\sigma_0^2} \right]
[/math]

なので[math]C=\frac{1}{\sqrt{2\pi\sigma_0^2}}[/math]とおくと尤度関数[math]L(\mu|\mathbf{x})[/math]は

[math]
\begin{eqnarray}
&& L(\mu|\mathbf{x})\\
&=& \prod_{i=1}^{n} f(x_i|\mu) \\
&=& C^n \exp\left[-\frac{1}{2\sigma_0^2}\sum_{i=1}^n (x_i-\mu)^2 \right]
\end{eqnarray}
[/math]

となります。

ここで、帰無仮説のパラメータ空間を

[math]
\Theta_0 = \left\{ \mu\ |\ \mu = \mu_0\right\}
[/math]

とおくと尤度比[math]\lambda(\mathbf{x})[/math]は定義より

[math]
\lambda(\mathbf{x}) = \dfrac{\sup_{\mu\in\Theta_0}L(\mu\ |\ \mathbf{x})}{\sup_{\mu\in\mathbb{R}}L(\mu\ |\ \mathbf{x})}
[/math]

となります。

まず、分母は対数尤度を微分して

[math]
\dfrac{d}{d\mu}\log L(\mu\ |\ \mathbf{x}) = \frac{1}{\sigma_0^2}\sum_{i=1}^n (x_i-\mu)=0
[/math]

を解くと[math]\mu^* = \dfrac{1}{n}\sum_{i=1}^n x_i(=\bar{x})[/math]の時、つまり標本平均[math]\bar{x}[/math]の時に最大値

[math]
\begin{eqnarray}
&& L(\mu^*\ |\ \mathbf{x}) \\
&=& C^n \exp\left[-\frac{1}{2\sigma_0^2}\sum_{i=1}^n (x_i-\bar{x})^2 \right]
\end{eqnarray}
[/math]

になることが分かります。

次に分子は[math]\Theta_0=\{\mu_0\}[/math]なので

[math]
\begin{eqnarray}
&& L(\mu_0\ |\ \mathbf{x}) \\
&=& C^n \exp\left[-\frac{1}{2\sigma_0^2}\sum_{i=1}^n (x_i-\mu_0)^2 \right]
\end{eqnarray}
[/math]

であり、平均[math]\bar{x}[/math]周りで展開し

[math]
\begin{eqnarray}
&&\sum_{i=1}^n (x_i-\mu_0)^2 \\
&=& \sum_{i=1}^n (x_i-\bar{x} + \bar{x}-\mu_0)^2 \\
&=& \sum_{i=1}^n (x_i-\bar{x})^2 + n (\bar{x}-\mu_0)^2
\end{eqnarray}
[/math]

となることに注意すると

[math]
\begin{eqnarray}
&& L(\mu_0\ |\ \mathbf{x}) \\
&=& L(\mu^*\ |\ \mathbf{x})\exp\left[-\frac{n}{2\sigma_0^2}(\bar{x}-\mu_0)^2 \right]
\end{eqnarray}
[/math]

が成立します。これより尤度比は

[math]
\lambda(\mathbf{x}) = \exp\left[-\frac{n}{2\sigma_0^2}(\bar{x}-\mu_0)^2 \right]
[/math]

と[math]|\bar{x}-\mu_0|[/math]の単調減少関数になっているので任意の定数[math]k > 0[/math]に対して定数[math]c > 0[/math]が存在して

[math]
\lambda(\mathbf{x}) \leq k \Leftrightarrow |\bar{x}-\mu_0| \geq c
[/math]

が成立するので尤度比検定は次の形に書くことができます。

正規母集団（分散既知）の平均に関する検定

事前に有意水準[math]\alpha[/math]を決め棄却域[math]R=\left\{\bar{x}\ |\ |\bar{x}-\mu_0| \geq c_\alpha\right\}[/math] を設定する。
標本平均[math]\bar{X}=\dfrac{1}{n}\sum_{i=1}^n X_i[/math]を計算する。
[math]\bar{X} \in R[/math]ならば帰無仮説を棄却し、そうでないなら帰無仮説を採択する。

帰無仮説の下では標本平均[math]\bar{X}\sim \mathcal{N}(\mu_0, \frac{\sigma_0^2}{n})[/math]になることから、両側検定の場合は標準正規分布[math]\mathcal{N}(0, 1)[/math]の上側[math]100\alpha / 2\%[/math]点[math]z_{\alpha/2}[/math]を使って棄却域[math]R[/math]を

[math]
R=\left\{\bar{x}\ |\ |\bar{x}-\mu_0| \geq \dfrac{\sigma_0}{\sqrt{n}}z_{\alpha / 2}\right\}
[/math]

と書けます。

例題の解答例

先ほどの例題を有意水準[math]\alpha=0.05[/math]として解いてみると[math]\mu = 119.6[/math], [math]\sigma_0 = 5.1[/math], [math]n=100[/math], [math]z_{0.025}=1.96[/math]より棄却域は

[math]
R=\left\{\bar{x}\ |\ |\bar{x}-119.6| \geq \dfrac{5.1\times 1.96}{\sqrt{100}}\right\}
[/math]

となります。標本平均[math]\bar{x} = 121.2[/math]なので棄却域に入り「全国平均とは異なると言える」という結果になります。