1.5 ベイズの定理

ベイズの定理

ある二つの事象[math]A, B[/math]が独立でない時、事象[math]B[/math]が生じたという情報を知ることで確率[math]P(A)[/math]は[math]P(A|B)[/math]に更新されます。各事象の確率と条件付き確率の関係を結びつけたのがベイズの定理（Bayes’ theorem）です。

証明は条件付き確率の定義式の分母を払うと

[math]
P(A\cap B)=P(A|B)P(B)
[/math]

で[math]A, B[/math]を入れ替えた

[math]
P(B\cap A)=P(B|A)P(A)
[/math]

も成立し、2式の左辺が等しいので右辺も等しく式変形することで上記の式が得られます。2つの条件付き確率[math]P(A|B), P(B|A)[/math]を同時確率[math]P(A\cap B)[/math]を通じて結びつけているわけですね。

この定理はベイズ統計学^[1]正直、勉強不足な領域なので不正確な記載があるかもしれません。の根幹をなす関係式です。ベイズ統計学では

• [math]P(A)[/math]: 何も情報がない時の事象[math]A[/math]の確率で「事前確率（prior probability）」
• [math]P(A|B)[/math]: 事象[math]B[/math]が生じたという情報を得た場合の事象[math]A[/math]の確率で「事後確率（posterior probability）」

と呼びます。事前確率[math]P(A)[/math]と事後確率[math]P(A|B)[/math]を結びつけているのがベイズの定理で、事前確率がどう変わる（増えるのか減るのか）かは条件付き確率[math]P(B|A)[/math]に比例することがわかります。では、このベイズの定理を応用した例を紹介します。

応用例（迷惑メールフィルタ）

事象[math]J, K[/math]を

• [math]J[/math]: メールが迷惑メールである
• [math]K[/math]: メールが特定キーワードを含む

とおくとキーワードが含まれているメールが迷惑メールである確率[math]P(J|K)[/math]はベイズの定理から[math]P(J|K)=\dfrac{P(K|J)}{P(K)}P(J)[/math]になります。

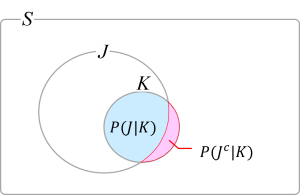
設定より[math]P(K|J), P(J)[/math]は既知で、残る[math]P(K)[/math]は迷惑メールか否かのMECEな場合分け、つまり

[math]
\begin{eqnarray}
K &=& K\cap (J\cup J^c) \\
&=& (K\cap J)\cup (K\cap J^c)
\end{eqnarray}
[/math]

と書いて確率を考えると

[math]
\begin{eqnarray}
&& P(K) \\
&=& P(K\cap J)+P(K\cap J^c) \\
&=& P(K|J)P(J)+P(K|J^c)P(J^c) \\
&=& 0.077
\end{eqnarray}
[/math]

より[math]P(J|K)=\dfrac{0.40}{0.077}\times 0.15=0.78[/math]と8割近い確率で迷惑メールになることが分かります。また、ベイズの定理の式から[math]P(J|K)[/math]を高めるキーワードとしては

• 全体としての出現頻度が低い（[math]P(K)[/math]が小）
• 迷惑メールには高い頻度で出現する（[math]P(K|J)[/math]が大）

ものを選ぶのが良いことが分かります。一方、通常メールを迷惑メールと誤判別するのを避けるために[math]P(J^c|K)[/math]を小さくする必要もあり

• 全体としての出現頻度が高い（[math]P(K)[/math]が大）
• 迷惑メール以外にはほとんど出現しない（[math]P(K|J^c)[/math]が小）

ようなキーワードを選ぶ必要があります^[3]さらに「一定数以上の迷惑メールを除きたい」という要件も考えられ、[math]P(K)[/math]を一定以上にするという条件も通常考慮されます。。つまり、迷惑メールに偏って出現するようなキーワードを設定すべきということがわかります。このように迷惑メールフィルタの性能評価のみならず設計方針を与えてくれる式としてベイズの定理は活用されています。

ベイズの定理の一般化

最後にベイズの定理を少し一般化した結果を紹介します。

ベイズ統計では事象[math]A[/math]が「関心のある事象」（例：迷惑メールか否か）で事象[math]B[/math]が「[math]A[/math]に関連する追加情報」と捉えます。関心のある事象[math]A[/math]が複数あるケース（例えば選択肢A, B, Cのどれが正解か）に一般化した結果が知られています。

証明は以下の2つに分けて考えると分かりやすいと思います。

1. [math]P(A_i|B)=\dfrac{P(B|A_i)}{P(B)}P(A_i)[/math]
2. [math]P(B)=\sum_{j=1}^{\infty}{P(B|A_j)P(A_j)}[/math]

前者はベイズの定理そのままで、後者は「迷惑メールフィルタ」の例と同様に事象[math]B[/math]を互いに排反な事象に分割し

[math]
\begin{eqnarray}
B &=& B\cap S \\
&=& B\cap \left(\cup_{j=1}^{\infty}A_j\right) \\
&=& \cup_{j=1}^{\infty}(B\cap A_j)
\end{eqnarray}
[/math]

その確率を考えるとコルモゴロフの公理と条件付き確率の定義から

[math]
\begin{eqnarray}
P(B) &=& \sum_{j=1}^{\infty}P(B\cap A_j) \\
&=& \sum_{j=1}^{\infty}{P(B|A_j)P(A_j)}
\end{eqnarray}
[/math]

を得ます。この式は「全確率の公式（law of total probability）」と呼ばれています。事象[math]B[/math]をMECEに場合分けをし、「各場合の条件付き確率」に「条件が生じる確率」の重みを付けて足しあわせた値が[math]P(B)[/math]になることを意味しており、複雑な事象の確率計算によく用いられます。

次の記事では「直感的に正しいと思える答えと論理的に正しい答えが異なる」と有名な「モンティ・ホール問題」を紹介したいと思います。

シリーズ記事

• 統計学
  • 1.4 条件付き確率と事象の独立
  • 1.5 ベイズの定理(本記事)
  • 1.6 確率変数

参考文献

• Casella, G and Berger, R.L.(1990), Statistical Inference(Second Edition): Section 1.3 Conditional Probability and Independence