確率変数 | 有意に無意味な話

ここから確率変数が登場し少し統計っぽくなってきます。

世論調査などで「ある政策について賛成・反対か？」を100人にアンケート調査する際は個別の回答が賛成かどうかよりも賛成の数（or 割合）に関心があります。100人の回答（賛成 or 反対）の標本空間は[math]2^{100}[/math]と膨大な組合せがありますが「賛成の数」は0〜100の101通りしかなく、より見通しよく結果を概観することができます。

このように元の標本（ex. 100人の回答）を何らかの演算で別の値に変換するものを確率変数(random variable)と呼びます。厳密には標本空間[math]S[/math]と[math]\sigma[/math]加法族上の確率関数[math]P[/math]が定義された確率空間において以下で定義されます。

標本空間[math]S[/math]を実数空間に写す関数を確率変数と呼ぶ。

例えば上の世論調査の例では、[math]i[/math]番目の人の回答を[math]q_i=1(賛成), 0(反対)[/math]と定義すると標本空間[math]S[/math]は[math]\{(q_1,\dots,q_{100})\ |\ q_i=0\ {\rm or}\ 1\}[/math]になり、各標本[math](q_1,\dots,q_{100})[/math]の賛成数[math]X[/math]は[math]X=\sum_{i=1}^{100}q_i[/math]とかけ、[math]X[/math]は[math]S[/math]を[math]\mathcal{X}=\{0,1,\dots,100\}[/math]に写す関数になっており定義から確率変数になっています。

数理統計学の大きな目的の1つは、標本空間[math]S[/math]と確率関数[math]P[/math]を設定した時（例：各回答者は賛成／反対を1/2の確率で答える）に確率変数[math]X[/math]がどのような値をどれくらいの確率でとるのか？を調べ、何らかの結論（例：賛成／反対が半々と考えるには不自然なくらい賛成が多い）を導くことです。

累積分布関数

確率変数[math]X: S\to\mathcal{X}[/math]の振る舞いを解析する上で非常に重要な役割を果たすのが累積分布関数(cumulative distribution function, cdf)で以下で定義されます。

確率変数[math]X[/math]に対して[math]F_X: \mathbb{R}\to [0,1][/math]を[math]F_X(x)=P(\{s\in S\ |\ X(s)\leq x\})[/math]で定義し累積分布関数と呼ぶ。

例えば上の例で各回答者は独立に確率[math]p[/math]で賛成と回答するとすると[math]F_X(x)[/math]は100人中[math]{\lfloor x \rfloor}[/math]人以下が賛成する確率になるので[math]x < 0[/math]だと[math]F(x)=0[/math], [math]x \geq 100[/math]だと[math]F(x)=1[/math], [math]0\leq x < 100[/math]だと

[math]F_X(x)=\sum_{k=0}^{\lfloor x \rfloor}{}_{100}C_{k}p^{k}(1-p)^{100-k}[/math]

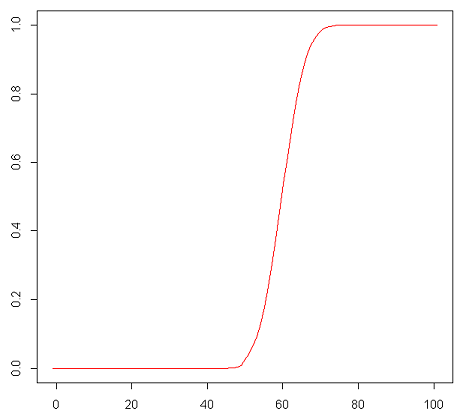
となります。[math]p=0.6[/math]の時の[math]F_X(x)[/math]のグラフを描くと以下になり60付近で急激に立ち上がり[math]X[/math]はおよそ60付近の値をとる確率が高いことが分かります。

累積分布関数を特徴付ける性質として以下の結果が知られています。

関数[math]F(x)[/math]が累積分布関数になるための必要十分条件は以下の3条件が成立することである。

[math]\lim_{x\to-\infty}F(x)=0[/math] かつ [math]\lim_{x\to\infty}F(x)=1[/math]
[math]F(x)[/math]は[math]x[/math]の非減少関数
[math]F(x)[/math]は右側連続、つまり任意の[math]x_0[/math]に対し[math]\lim_{x\downarrow x_0}F(x)=F(x_0)[/math]

必要性は確率関数の性質から導くことができますが、十分性（3つの性質を満たす関数[math]F(x)[/math]が存在した時に、標本空間[math]S[/math]と確率関数[math]P[/math]が存在して累積分布関数が[math]F[/math]となるような確率変数[math]X[/math]が定義できること）の証明は難しいようでStatistical Inferenceでも割愛されているのでここでも割愛します。

最後に累積分布関数が確率変数の振る舞いを完全に表現していることを示す定理を紹介します。まず、2つの確率変数の同一分布性を定義します。

2つの確率変数[math]X, Y[/math]が同一分布に従う(identically distributed)とは1次元の[math]\sigma[/math]加法族[math]\mathcal{B}^1[/math]の任意の[math]A\in\mathcal{B}^1[/math]に対して[math]P(X\in A)=P(Y\in A)[/math]が成立することである。

少し注意が必要なのは上の定義は必ずしも[math]X=Y[/math]を意味していないということです。例えば上の例で[math]p=1/2[/math]と時を考え[math]X[/math]を「賛成の数」、[math]Y[/math]を「反対の数」とすると賛成と反対がちょうど50人ずつになるケースを除いて

[math]X(s)\ne Y(s),\ s\in S[/math]

ですが

[math]P(X\leq k)=P(Y\leq k),\ \forall k[/math]

なので上記定義を満たして2つの確率変数[math]X, Y[/math]は同一分布に従うといえます。

確率変数が同一分布に従うことと累積分布関数の関係を示した以下の定理が知られています。

2つの確率変数が同一分布に従うための必要十分条件は任意の[math]x\in\mathbb{R}[/math]について[math]F_X(x)=F_Y(x)[/math]が成立することである。

つまり、確率変数が同一分布に従うかどうかは累積分布関数が等しくなるかどうかで判定できることが分かります。なお、証明については必要性は[math]A=(-\infty,x)[/math]を考えることで簡単に示せますが、十分性は[math]\sigma[/math]加法族に関する結果を使う必要がありStatistical Inferenceでも割愛^[1]詳しく知りたい方はChung, K. L.(1974), A Cource in Probability Theoryを参照とのこと。されているのでここでも割愛します。