【統計検定1級過去問】2018年（理工学）大問2

形状パラメタ[math]m > 0[/math]と尺度パラメタ[math]\eta > 0[/math]を持つワイブル分布[math]W(m,\eta)[/math]の累積分布関数[math]F(x)[/math]は

[math]

F(x) = \begin{cases}
1-\exp \left[-(x / \eta)^{m}\right] &(x \geq 0) \\
0 &(x < 0) \end{cases} [/math]

で与えられる。以下の問いに答えよ。

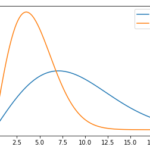
1. [math]W(m,\eta)[/math]の確率密度関数[math]f(x)[/math]、最頻値を求めよ。また、[math]W(2, 10), W(2, 5)[/math]の概形を図示せよ。
2. [math]W(m,\eta)[/math]のハザード関数[math]h(x)=\frac{f(x)}{1-F(x)}[/math]を求め[math]m[/math]の値による[math]h(x)[/math]の特徴を論ぜよ。
3. [math]k[/math]個の部品からなる直列システムにおいて各部品の寿命は互いに独立で[math]W(m,\eta)[/math]に従うとする。このシステムは1つの部品でも故障すると稼働を停止する。このシステムが稼働停止するまでの時間が従う分布を求めよ。
4. 確率変数[math]X \sim W(2, 10)[/math], [math]Y \sim W(2,5)[/math]は互いに独立とする。この時、[math]P(X < Y)[/math]を求めよ。
5. 寿命が互いに独立に[math]W(m,\eta)[/math]に従う[math]n[/math]個の部品の寿命試験を行い観測値[math]x_1,\dots,x_n[/math]を得た。[math]W(m,\eta)[/math]のパラメタ[math]m,\eta[/math]の対数尤度関数を示せ。また、[math]\log\log\dfrac{1}{1-F(x)}[/math]を求めパラメタを推定する方法を論ぜよ。