【統計検定1級過去問】2018年（理工学）大問2 解答例

コメント

ワイブル分布を用いた信頼性解析がテーマでした。

問3の順序統計量（最小値）の分布を求めるのと、問4の確率計算がやや難しいですが丁寧な誘導がついており部分点を十分取れた問題セットだと思います。

問題

（出典：統計検定HP「統計検定 1級の過去問題」。問題文を一部略記。）

問1

確率密度関数[math]f(x)[/math]は

[math]
\begin{eqnarray}

f(x) &=& \dfrac{d}{dx}F(x) \\
&=& \dfrac{m}{\eta} \cdot\left(\dfrac{x}{\eta}\right)^{m-1}\exp\left[-\left(\dfrac{x}{\eta}\right)^{m}\right]
\end{eqnarray}
[/math]

である。最頻値を求めるため[math]f'(x)[/math]を計算すると

[math]

f'(x)=\dfrac{m x^{m-2}}{\eta^{m}}\left\{(m-1)-\dfrac{m x^{m}}{\eta^{m}}\right\}\exp\left[-\left(\dfrac{x}{\eta}\right)^{m}\right]
[/math]

なので[math]f'(x)=0[/math]を解いて[math]x=\left(\dfrac{m-1}{m}\right)^{1/m}\eta[/math]が最頻値である。

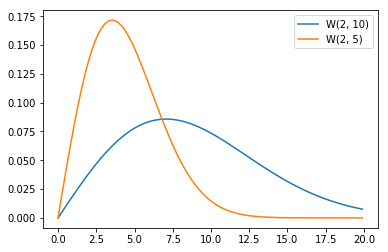
[math]W(2, 10), W(2, 5)[/math]の概形を求めると

• [math]W(2, 10)[/math]: [math]10/\sqrt{2}[/math]で最大値
• [math]W(2, 5)[/math]: [math]5/\sqrt{2}[/math]で最大値
• [math]\eta[/math]の大きい[math]W(2, 10)[/math]の方が[math]W(2, 5)[/math]より右に裾の長い分布になる

に留意すると以下の図になる。

問2

ハザード関数[math]h(x)[/math]を求めると

[math]

h(x)=\dfrac{f(x)}{1-F(x)}=\dfrac{m}{\eta} \cdot\left(\dfrac{x}{\eta}\right)^{m-1}
[/math]

になる。これより[math]h(x)[/math]の特徴は

• [math]m < 1[/math]: 単調減少関数
• [math]m = 1[/math]: 定数
• [math]m > 1[/math]: 単調増加関数

になる。

問3

システムが稼働停止するまでの時間を[math]T[/math]とすると

[math]

T = \min(X_1,\dots,X_k)
[/math]

であり[math]T \leq t[/math]となるのは「[math]X_i[/math]のいずれかが[math]t[/math]以下」の時なので

[math]
\begin{eqnarray}
P(T \leq t) &=& 1 – 
P(X_1 > t)\cdot \cdots \cdot P(X_k > t) \\
&=& 1 – \left(1 – F(t)\right)^k \\
&=& 1 – \exp\left[-\left(\dfrac{x}{\eta k^{-1/m}}\right)^m \right]
\end{eqnarray}
[/math]

を得る。 これはパラメタ[math](m, \eta k^{-1/m})[/math]のワイブル分布の累積分布関数なのでシステムが稼働停止するまでの時間はパラメタ[math](m, \eta k^{-1/m})[/math]のワイブル分布に従う。

問4

[math]W(m,\eta)[/math]の確率密度関数を[math]f(x;m,\eta)[/math]と書く。[math]X \sim W(m, \eta_1), Y \sim W(m, \eta_2)[/math]とすると

[math]
\begin{eqnarray}



&& P(X < Y) \\ &=& \displaystyle\int_0^\infty f(x; m,\eta_1) \int_x^\infty f(y; m,\eta_2)dydx \end{eqnarray} [/math]

と書け

[math]
\begin{eqnarray}
&& 
\displaystyle\int_x^\infty f(y; m,\eta_2)dy \\
&=& 1 – F(x; m,\eta_2) = \exp\left[-\left(\dfrac{x}{\eta_2}\right)^m\right]

\end{eqnarray}
[/math]

なので

[math]
\begin{eqnarray}
&& 




P(X < Y) \\ &=& \displaystyle\int_0^\infty \left(\frac{m}{\eta_{1}}\right)\left(\frac{x}{\eta_{1}}\right)^{m-1}\exp\left[-\left(\dfrac{1}{\eta_1^m}+\dfrac{1}{\eta_2^m}\right)x^m\right]dx \end{eqnarray} [/math]

となり[math]\hat{\eta}=\left(\frac{1}{\eta_{1}^{m}}+\frac{1}{\eta_{2}^{m}}\right)^{-1 / m}[/math]とおくと

[math]
\begin{eqnarray}





&& P(X < Y) \\ &=& \dfrac{\hat{\eta}^m}{\eta_1^m} \int_0^\infty \dfrac {m}{\hat{\eta}}\left(\dfrac{x}{\hat{\eta}}\right)^{m-1}\exp\left[-\left(\dfrac{x}{\hat{\eta}}\right)^m\right]dx \\ &=& \dfrac{\hat{\eta}^m}{\eta_1^m}\int_0^\infty f(x; m,\hat{\eta})dx \\ &=& \dfrac{\hat{\eta}^m}{\eta_1^m} \\ &=& \dfrac{\eta_2^m}{\eta_1^m + \eta_2^m} \end{eqnarray} [/math]

となる。[math]m=2, \eta_1=10, \eta_2=5[/math]を代入して[math]P(X < Y)=\dfrac{1}{5}[/math]である。

問5

まず確率密度関数の対数は

[math]

\log f(x)=\log m+(m-1) \log x – m \log \eta-\left(\dfrac{x}{\eta}\right)^{m}
[/math]

なので対数尤度関数は

[math]
\begin{eqnarray}

&& 
\log L(m,\eta) \\
&=& n\log m+(m-1) \sum_{i=1}^n\log x_i – mn \log \eta-\sum_{i=1}^n\left(\dfrac{x_i}{\eta}\right)^{m}
\end{eqnarray}
[/math]

である。

次に[math]\dfrac{1}{1-F(x)}=\exp\left[\left(\dfrac{x}{\eta}\right)^m\right][/math]なので

[math]

\log \log \dfrac{1}{1-F(x)} = m\log x – m\log \eta
[/math]

が成立する。これより[math]\left(\log x_i, 
\log \log \dfrac{1}{1-F(x_i)}\right)[/math]をプロットし

• [math]m[/math]: 傾きから推定
• [math]\eta[/math]: 切片と[math]m[/math]から推定

できる。

シリーズ記事

• 過去問と解答例
• 2018年（理工学）大問1
• 2018年（理工学）大問1 解答例
• 2018年（理工学）大問2
• 2018年（理工学）大問2 解答例(本記事)
• 2018年（理工学）大問5
• 2018年（理工学）大問5 解答例