年末に録画していた大人のピタゴラスイッチ「ピーマンとハトと数学」を見ました。「大人の」とついてますが、子供にも面白さ、凄さが伝わる番組だと思います。「ビーだまビーすけの大冒険」もピタゴラ装置もさることながらストーリーも面白かったですね。
さて、サブタイトルの「ピーマンとハトと数学」のピーマンって一体??と思っていたら「重さにばらつきがあるピーマン(20〜50g/個)をうまく組合せて特定の重さ(150g)に袋詰めするには?」という話でした。
組合せ計量装置
ピーマン1個1個の重さを計りながら150gの組み合わせを人手で見つけるのは大変ですが、世の中には「組合せ計量装置」というどストレートなネーミングをした便利マシンがあります。以前この機械を開発している人と話す機会があり
「役に立つものを作ってると思うけど一般の人に知ってもらう機会がなくて奥さんや親戚に説明するのに苦労するんだよねぇ」
と言っていましたがこの番組に取り上げてもらえると一気に知名度が上がっていいですね。
さて、この「組合せ計量装置」のコンベア上にピーマンを乗せると

各コンベアのピーマンの重さを計り

指定した重さ150gになるピーマンの組合せを自動で選んで

袋詰めをしてくれるのです。
指定した重さになる組合せを見つけること自体は12個のコンベア上にあるピーマンを選ぶ/選ばないの2択なので総当たりでも[math]2^{12}=4096[/math]通りしかなく計算機には簡単です。
少し気になるのは通常指定した重さになる組合せは複数ある[1]150g未満の組合せを売ってしまうとクレームにつながりますが多少の上ブレは許容されるはずで許容解は複数存在すると考えられます。のでどのピーマンを使うか?(どのピーマンを残しておくか?)は重さに偏りのあるピーマンを使えるときに使っておくべきなのか、多様性を維持するために残しておくべきなのかを考えるとポリシー作りは結構難しいのではと思っていました。ただ、開発者によると
「複雑なポリシーにしてもシンプルなポリシーと比べてあまり差がでず工数をかけるメリットが少ない」
らしくシンプルなポリシーになっているようです[2]2000年代の話なので今は違っているかもしれません。。ちなみにピーマンのような固体ではなく味噌のような粘性の高い物の場合、計量→パッケージングの過程で装置に付着する量にブレがあるため狙った重さの組合せを作るのが難しいそうです。組合せ計量装置の世界も奥が深いですね。
「組合せ」の威力
狙った重さの組合せを高確率で見つけられることを番組ではサイコロを使って説明していました。具体例として
と紹介されており、番組中でもラーメンズの片桐さんがサイコロを実際に投げて

1投目は「1, 2, 5, 5, 6, 6」で5+5で10が作れ

2投目も「2, 4, 5, 5, 6, 6」で4+6や5+5で10が作れていました。
6個のサイコロを振ったときの目の場合の数は[math]6^6=46,656[/math]通りあり、和が[math]k(k=1,2,\dots,36)[/math]になる場合の数を計算[3]動的計画法で求めました。すると以下になります。
ここから
- [math]k=10[/math]を作れる確率は[math]45,674/46,656=0.9789\cdots[/math]と確かに約98%ある
- もっとも作れる確率が高いのは[math]k=6[/math]の時で99.1%
- 少なくとも2つのサイコロを使う必要がある[math]k\geq 7[/math]で作れる確率がもっとも高いのは[math]k=12[/math]で98.3%、二番目に高いのが[math]k=10[/math]の時で97.9%
- [math]4\leq k\leq 15[/math]だと90%以上の確率で作れる
- いずれの[math]k[/math]でも100%になることはない
といったことが分かります。番組的には「うまく組合せを見つけると狙った数を作れる」ということが言いたいので、作れる可能性が高い[math]k=6[/math]が良い気がしますが[math]k=6[/math]だとサイコロ1つで作れてしまうケースがあり「うまく組合せを見つけると」の部分が伝わりにくいので少し大きめの[math]k=10[/math]を選んだのかも知れませんね。もちろん100%ではないので例えば
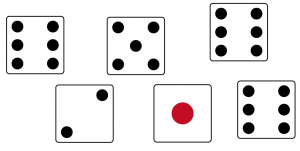
ではどのように組み合わせても10を作ることはできません。(1と2では3までしか作れず、5 or 6を1つだけ使う必要があることとあわせると10が作れないことが分かります)
冷静に考えると6個の目はそれなりにばらけるハズでその組合せ(4,096通り)の和もそれなりにばらけるので、[math]k[/math] が極端に大きい/小さい値でなければほぼ確実に作ることができるのも納得できます。多様性と組合せの威力ですね。
「鳩」の威力
[math]k=10[/math]についてはいかに多様性があり組合せの柔軟性があったとしても6個振ろうが100個振ろうが和を10にできる確率は100%にはなりません[4]100個の目がすべて6になるなど10が作れないケースが存在するため。。
では、他の[math]k[/math]についてはどうなるのか?を考えると、ピーマンの話に次に出た「鳩」の話(鳩ノ巣原理)を使うと次のことが分かります。
考え方としては
- 59個のサイコロが入る1と書かれた壷
- 29個のサイコロが入る2と書かれた壷
- 19個のサイコロが入る3と書かれた壷
- 14個のサイコロが入る4と書かれた壷
- 11個のサイコロが入る5と書かれた壷
- 9個のサイコロが入る6と書かれた壷
を用意し、142個のサイコロを振り、出た目の数と同じ数字が書かれた壷に入れていきます。[math]59+29+19+14+11+9=141[/math]なので鳩ノ巣原理から少なくとも1つの壷はサイコロがあふれることになります。例えば2の壷があふれたとすると2の目のサイコロが29+1個以上あるのでその壷から30個のサイコロを選ぶとその和は[math]2\times 30=60[/math]になります。他の数字の壷があふれた場合についても同様に60[5]60は[math]1,2,\dots,6[/math]の最小公倍数です。[math]k < … Continue readingを作れることが分かります。 ピーマンと鳩、一見関係なさそうですが色々考えると話がつながるおもしろい番組でした。
脚注
| ↑1 | 150g未満の組合せを売ってしまうとクレームにつながりますが多少の上ブレは許容されるはずで許容解は複数存在すると考えられます。 |
|---|---|
| ↑2 | 2000年代の話なので今は違っているかもしれません。 |
| ↑3 | 動的計画法で求めました。 |
| ↑4 | 100個の目がすべて6になるなど10が作れないケースが存在するため。 |
| ↑5 | 60は[math]1,2,\dots,6[/math]の最小公倍数です。[math]k < 60[/math]だと[math]k[/math]と互いに素な数字の目が出続けると和を[math]k[/math]に出来ないので100%の確率で和を作ることができる数の最小値が60であることが分かります。 |