確率の基本的性質 | 有意に無意味な話

確率の性質

コルモゴロフの公理から確率の各種性質を導びけます。まず集合とその補集合の関係についてです。

[math]P[/math]を[math]\sigma[/math]加法族[math]\mathcal{B}[/math]上の確率関数とする。任意の[math]A\in \mathcal{B}[/math]に対し以下が成立する。

[math]P(A)+P(A^c)=1[/math]
[math]P(A)\leq 1[/math]
[math]P(\emptyset)=0[/math]

1つ目は[math]A,A^c[/math]は互いに排反であり、[math]S=A\cup A^c[/math]であることから示せ、2つ目は1つ目と[math]P(A^c)\geq 0[/math]であることから示せ、3つ目は1つ目の等式において[math]A=S[/math]とすることで示せます。

次に2つの集合の関係についてです。

[math]P[/math]を[math]\sigma[/math]加法族[math]\mathcal{B}[/math]上の確率関数とする。任意の[math]A,B\in \mathcal{B}[/math]に対し以下が成立する。

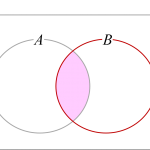
[math]P(B)=P(B\cap A^c)+P(A\cap B)[/math]
[math]P(A\cup B)=P(A)+P(B)-P(A\cap B)[/math]
[math]A\subset B[/math]ならば[math]P(A)\leq P(B)[/math]

公理の3つ目の性質から互いに排反な事象の「和集合の確率」は「個別事象の確率の和」になるので互いに排反な集合として表現するのがポイントです。

1つ目は集合[math]B[/math]を[math]A[/math]との共通部分とそれ以外に分ける、つまり[math]B=(A\cap B)\cup (B \cap A^c)[/math]と書いてその確率を考えることで示せます。

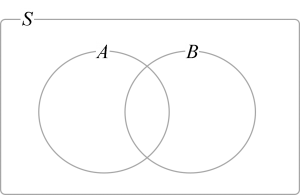
同様に2つ目も[math]A\cup B[/math]を[math]A[/math]とそれ以外に分けて[math]A\cup B=A\cup (B \cap A^c)[/math]と排反な集合の和集合で書けるのでその確率と1つ目の結果を使って示せます。集合間の関係はベン図を使うと理解しやすいと思います。

3つ目は[math]A\subset B[/math]ならば[math]A\cap B=A[/math]なので1つ目の等式から[math]P(B)=P(B\cap A^c)+P(A)\geq P(A)[/math]が示せます。

Bonferroniの不等式、Booleの不等式

最後に和集合、積集合の確率を個別事象の確率で評価する不等式を紹介します。2つの集合の和集合、積集合については以下が成立します。

[math]P[/math]を[math]\sigma[/math]加法族[math]\mathcal{B}[/math]上の確率関数とする。任意の[math]A,B\in \mathcal{B}[/math]に対し以下が成立する。

[math]\max\{P(A), P(B)\}\leq P(A\cup B)\leq P(A)+P(B)[/math]
[math]P(A)+P(B)-1\leq P(A\cap B)\leq \min\{P(A), P(B)\}[/math]

1つ目の和集合の確率評価は下側は[math]A\subset A\cup B, B\subset A\cup B[/math]から得られ、上側は

[math]
P(A\cup B)=P(A)+P(B)-P(A\cap B)
[/math]

と[math]P(A\cap B)\geq 0[/math]から得られます。

2つ目の積集合の確率評価は下側は

[math]
P(A\cap B)=P(A)+P(B)-P(A\cup B)
[/math]

と[math]P(A\cup B)\leq 1[/math]から、上側は[math]A\cap B\subset A, A\cap B\subset B[/math]から得られます。

積集合の下側の不等式

[math]
P(A)+P(B)-1\leq P(A\cap B)
[/math]

はBonferroniの不等式と呼ばれます。[math]P(A),P(B)[/math]の値が小さいと[math]P(A)+P(B)-1[/math]が0より小さくなって自明な不等式になりますが、[math]P(A)=0.95, P(B)=0.85[/math]のときは

[math]
P(A\cap B)\geq 0.95+0.85-1=0.8
[/math]

と確率の高い事象の同時確率を簡単に評価することができます。この結果を一般化したBooleの不等式と呼ばれる結果が知られています。

[math]P[/math]を[math]\sigma[/math]加法族[math]\mathcal{B}[/math]上の確率関数とする。任意の[math]A_1,A_2,\dots\in \mathcal{B}[/math]に対し以下が成立する。
[math]P\left(\bigcup_{i=1}^\infty A_i\right)\leq \sum_{i=1}^\infty P(A_i)[/math]

証明の方針としては「確率の性質」の節と同様に互いに排反な事象列[math]\{A_i^*\}[/math]で[math]\bigcup_{i=1}^\infty A_i=\bigcup_{i=1}^\infty A_i^*[/math]となるものを構成し不等式評価を行います。

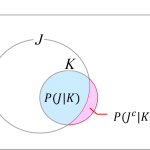
具体的には[math]\bigcup_{j=1}^{i-1} A_j[/math]から[math]\bigcup_{j=1}^{i} A_j=A_i\cup \bigcup_{j=1}^{i-1} A_j[/math]に「新たに増える部分」、つまり[math]A_i^*=A_i \cap \left(\bigcup_{j=1}^{i-1} A_j\right)^c[/math]という事象列を考えます。ベン図で考えると薄青部が[math]A_i^*[/math]に対応します。

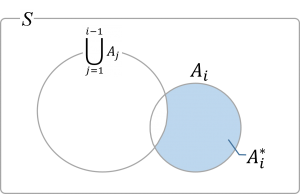
この事象列[math]\{A_i^*\}[/math]について

[math]A_1^*, A_2^*, \dots[/math]は互いに排反
[math]A_i^*\subset A_i[/math]
任意の[math]n[/math]について[math]\bigcup_{i=1}^n A_i=\bigcup_{i=1}^n A_i^*[/math]

を示すことで

[math]
\begin{eqnarray}
&& P\left(\bigcup_{i=1}^\infty A_i\right) \\
&=& P\left(\bigcup_{i=1}^\infty A_i^*\right) \\
&=& \sum_{i=1}^\infty P(A_i^*) \\
&\leq & \sum_{i=1}^\infty P(A_i)
\end{eqnarray}
[/math]

が得られます。

Booleの不等式を使って積集合に関する評価であるBonferroniの不等式を一般化できます。ド・モルガンの法則[math]\bigcap_{i=1}^n A_i=\left(\bigcup_{i=1}^n A_i^c\right)^c[/math]と[math]P(A_i^c)=1-P(A_i)[/math]から

[math]
\begin{eqnarray}
&& P\left(\bigcap_{i=1}^n A_i\right) \\
&=& 1-P\left(\bigcup_{i=1}^n A_i^c\right) \\
&\geq & 1-\sum_{i=1}^nP(A_i^c) \\
&=& \sum_{i=1}^nP(A_i)-(n-1)
\end{eqnarray}
[/math]

が得られ、[math]n=2[/math]の時がBonferroniの不等式になっていることがわかります。