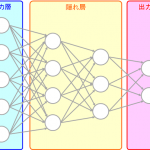
ニューラルネットワーク(Neural Network, NN)とは脳の神経細胞(ニューロン, Neuron)の挙動をモデル化し、物体認識や判別などの脳機能を計算機上でシミュレーションすることを目指したモデルです。もう少し具体的には
- ユニット(unit): 神経細胞を数学的にモデル化
- ニューラルネットワーク: ユニットをつなぎ合わせて神経回路網をモデル化
という構成になっており、まずは最も基本的な要素である「ユニット」と呼ばれるニューロンの数学モデルについて定義します。
ユニットの定義
生物学の知見から脳の神経細胞は以下の挙動をすることが知られています。
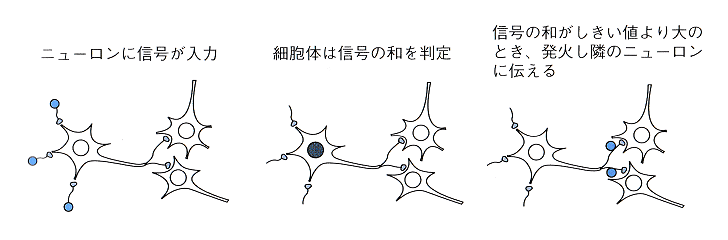
(出典:「ディープラーニングがわかる数学入門」P.11)
- 神経細胞は他の複数の神経細胞とつながっており、信号を受け取りその大きさに応じて反応を行う
- 他の神経細胞からの信号の和が一定のしきい値を超えなければ反応しない
- 他の神経細胞からの信号の和が一定のしきい値を超えれば反応し別の神経細胞に一定の強さの信号を伝える
- 2, 3において信号の和は信号ごとにその重みが異なる
この神経細胞の挙動を数学的にモデル化したものがユニットになります。まず他の神経細胞が[math]n[/math]個あるとし、その信号を[math]\mathbf{x}=(x_1,\dots,x_n)[/math]とします。4.の「信号ごとの重み(weight)」を[math]\mathbf{w}=(w_1,\dots,w_n)[/math]とすると「他の神経細胞からの信号の和[math]S[/math]」は
[math]
\begin{eqnarray}
S &=& w_1x_1 + \cdots + w_nx_n \\
&=& \mathbf{w}^T \mathbf{x}
\end{eqnarray}
[/math]
になります。
神経細胞の反応[math]y[/math]を
- 反応有り: [math]y=1[/math]
- 反応無し: [math]y=0[/math]
と対応づけ「一定のしきい値」を[math]\theta[/math]とすると
[math]
y = \begin{cases}1 &(S > \theta) \\ 0 &(S \leq \theta)\end{cases}
[/math]
と表現できます。この「信号の和[math]S[/math]」と「しきい値[math]\theta[/math]」から出力を求める関数を活性化関数(activation function)と呼びます。
生物学的には[math]x_i, w_i[/math]や[math]y[/math]は正の値をとるのが自然ですが、ニューラルネットワークでは数学的な取り扱いの容易さなどの観点から特に制限せず実数として定義します。また、活性化関数も様々な関数が考えられるため一般の実数値関数として定義します。
以上をまとめてニューロンの数学モデルであるユニットを定義します。
- 重み: [math]\mathbf{w}=(w_1,\dots,w_n)\in\mathbb{R}^n[/math]
- しきい値: [math]\theta\in\mathbb{R}[/math]
- 活性化関数: [math]a: \mathbb{R}\to\mathbb{R}[/math]
を用いて[math]y = a(\mathbf{w}^T \mathbf{x} – \theta)[/math]で与えられる。
なお、活性化関数の引数で[math]\theta[/math]の符号だけ負で計算が煩雑なので
[math]
y = a(\mathbf{w}^T \mathbf{x} + b)
[/math]
と表記することが一般的です。この[math]b(=-\theta)[/math]をバイアス(bias)と呼びます。さらに簡潔に表記するため[math]\mathbf{x}’=(1, x_1,\dots,x_n)[/math], [math]\mathbf{w}’=(b, w_1,\dots,w_n)[/math]とおいて
[math]
y = a(\mathbf{w}’^T \mathbf{x}’)
[/math]
とすることもあります。この場合も[math]\mathbf{x}’, \mathbf{w}'[/math]をそれぞれまとめて「入力」「重み」と呼びます。
ユニットの表記方法
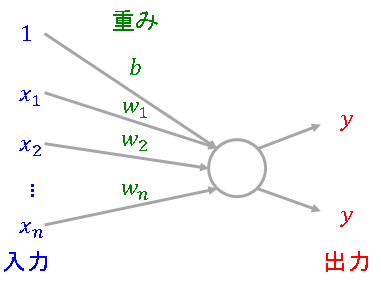
ニューラルネットワークを図示するには多数のユニットを表現するため以下の簡略化した図で示すことが一般的です。
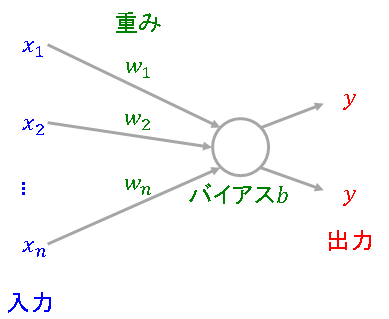
上図は重みとバイアスを分けていますが、まとめる場合は下図の描き方をします。
シリーズ記事
- ニューラルネットワークの基本要素:ユニット(本記事)
- ニューラルネットワークの構造とその歴史
- 単純パーセプトロンの収束定理と限界
参考文献
- 涌井 良幸・涌井 貞美 著(2017年)「ディープラーニングがわかる数学入門
」(技術評論社)