単純パーセプトロンの収束定理と限界

ニューラルネットワーク(Neural Network, NN)の基本形と言える単純パーセプトロン(simple perceptron)が持つ能力とその限界について紹介します。

単純パーセプトロンの定義

まず単純パーセプトロンで取り扱う「2値分類問題」について定義します。

例えばECサイトにおける顧客[math]i[/math]の購買履歴データ[math]\mathbf{x}_i[/math]と優良顧客フラグ[math]y_i[/math]を用意し、優良顧客([math]y=1[/math])か否（[math]y=-1[/math]）かを判別する基準を求めておけば、新しい顧客の購買履歴データから優良顧客になりそうかを判断できるようになります。

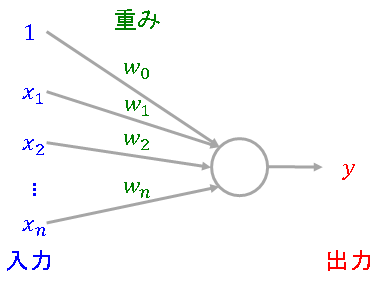
単純パーセプトロンは[math](n+1)[/math]個の入力[math]\mathbf{x}’=(1, x_1,\dots,x_n)\in\mathbb{R^{n+1}}[/math]を受け取り^[1] … Continue reading、入力値にモデルのパラメータ

• 重み(weight): [math]\mathbf{w}=(w_0, w_1,\dots,w_n)\in\mathbb{R^{n+1}}[/math]

を掛け合わせた値が0を超えていれば[math]1[/math]、そうでなければ[math]-1[/math]を出力するモデルで、図示すると以下になります。以降、バイアス項を含めた[math]\mathbf{x}'[/math]を単に[math]\mathbf{x}[/math]と表記します。

数式で書くと

[math]
\begin{eqnarray}
y &=& a(\mathbf{w}^T \mathbf{x}) \\
a(x) &=& \begin{cases}1 &(x\geq 0) \\ -1 &(x < 0) \end{cases} \end{eqnarray} [/math]

になります。重みと入力値を掛け合わせた値から出力に変換する関数[math]a(x)[/math]を活性化関数(activation function)と呼び、単純パーセプトロンではステップ関数を用います。

単純パーセプトロンの学習アルゴリズム

単純パーセプトロンではうまく分類出来なかった教師データ[math](\mathbf{x}_i,\ y_i)[/math]に対してパラメータ[math]\mathbf{w}[/math]の修正を行うことを繰り返します。具体的には次のアルゴリズムでパラメータの修正（学習）を行います。

パーセプトロンの学習方法のポイントは5.の分類が誤った場合の更新方法です。正しいラベル[math]y_i=1[/math]に対して[math]y_i^k=-1[/math]となった、つまり[math]\mathbf{w}^T\mathbf{x}_i\geq 0[/math]となるべき所が

[math]
\mathbf{w}^T\mathbf{x}_i < 0 [/math]

となってしまった事例に対し重み[math]\mathbf{w}[/math]を更新し

[math]
\begin{eqnarray}
{\mathbf{w}^{k+1}}^T\mathbf{x}_i &=& (\mathbf{w}^k + \eta \mathbf{x}_i)^T \mathbf{x}_i \\
&=& {\mathbf{w}^k}^T\mathbf{x}_i + \eta || \mathbf{x}_i ||^2 \\
& > & {\mathbf{w}^k}^T\mathbf{x}_i \quad (\because \mathbf{x}_i\ne 0)
\end{eqnarray}
[/math]

と誤りを改善するように重みを調整します。（[math]y_i=-1[/math]についても同様に改善することを示せます。）

重みを更新することで間違えた事例[math]i[/math]の判別が改善しますが、他の事例[math]j(\ne i)[/math]が改悪されてしまう可能性があります。しかし、ある種の問題では全体としてうまく修正が進み正しい判別基準が得られることが知られています。詳細を紹介する前に単純パーセプトロンの挙動を見てみましょう。

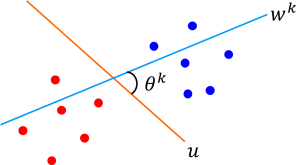
青い点と赤い点を判別するための基準線を上記の学習ルールに沿って更新していく様子をアニメーションにしています。4回の更新で青い点と赤い点を完全に識別する基準線を見事に見つけてくれています。

このように「間違いがあれば修正する」という単純なルールを繰り返すだけで「青い点／赤い点の判別能力を獲得できる」ことが分かり非常に大きな注目を集めました。

単純パーセプトロンの収束定理

では、単純パーセプトロンはどのような問題を解くことが出来るのでしょうか？

その答えとして、上の例のように分類対象が直線で分離可能な場合^[2]線形分離可能といいますには単純パーセプトロンは識別する基準を必ず見つけてくれること（「パーセプトロンの収束定理」）が知られています。

まず教師例の正例/負例集合を[math]I^+=\{i\ |\ y_i=1\}[/math], [math]I^-=\{i\ |\ y_i=-1\}[/math]とします。

教師例は線形分離可能なので[math]\mathbf{u}\in\mathbb{R}^{n+1}[/math]と[math]\gamma > 0[/math]が存在して

[math]
\begin{eqnarray}
\mathbf{u}^T \mathbf{x}_i \geq &\gamma& \quad \forall i \in I^+ \\
\mathbf{u}^T \mathbf{x}_i \leq &-\gamma& \quad \forall i \in I^-
\end{eqnarray}
[/math]

が成立します。また、[math]\|\mathbf{u}\|=1[/math]として一般性を失いません。

[math]k[/math]回目の反復で求められた重み[math]\mathbf{w}[/math]と[math]\mathbf{u}[/math]のなす角を[math]\theta^k[/math]とし

[math]
\cos \theta^k = \dfrac{\mathbf{u}^T\mathbf{w}^k}{\|\mathbf{w}^k\|} \quad (\because \|\mathbf{u}\|=1)
[/math]

を評価します。

ここでは簡単のために重みの初期値[math]\mathbf{w}^0=0[/math]の場合について示します。[math]k-1[/math]回目の反復で事例[math]j \in I^+[/math]の誤りを修正したとすると

[math]
\begin{eqnarray}
\mathbf{u}^T\mathbf{w}^k &=& \mathbf{u}^T(\mathbf{w}^{k-1}+\eta\mathbf{x}_j)\\
&=& \mathbf{u}^T\mathbf{w}^{k-1} + \eta \mathbf{u}^T\mathbf{x}_j \\
&\geq& \mathbf{u}^T\mathbf{w}^{k-1} + \eta \gamma
\end{eqnarray}
[/math]

が成立します。[math]j \in I^-[/math]の場合も同じ不等式が成立することを示せます。これより

[math]
\begin{eqnarray}
\mathbf{u}^T\mathbf{w}^k &\geq &\mathbf{u}^T \mathbf{w}^{k-1} + \eta \gamma \\
&\vdots&\\
&\geq & \mathbf{u}^T\mathbf{w}^0 + k \eta \gamma \\
&=& \eta k \gamma
\end{eqnarray}
[/math]

が成立します。

次に分母[math]\|\mathbf{w}^k\|[/math]を評価します。[math]\|\mathbf{x}_i\|[/math]の最大値を[math]D[/math]とし、[math]k-1[/math]回目の反復で事例[math]j \in I^+[/math]の誤りを修正したとすると[math]{\mathbf{w}^{k-1}}^T \mathbf{x}_j < 0[/math]であることに注意すると

[math]
\begin{eqnarray}
&& \|\mathbf{w}^k\|^2 \\
&=& \|\mathbf{w}^{k-1}+\eta\mathbf{x}_j\|^2 \\
&=& \|\mathbf{w}^{k-1}\|^2 + \eta^2 \|\mathbf{x}_j\|^2\\
&&\quad + 2\eta{\mathbf{w}^{k-1}}^T \mathbf{x}_j \\
&\leq & \|\mathbf{w}^{k-1}\|^2 + \eta^2 \|\mathbf{x}_j\|^2 \\
&\leq & \|\mathbf{w}^{k-1}\|^2 + \eta^2D^2
\end{eqnarray}
[/math]

が成立します。[math]j \in I^-[/math]の場合も同じ不等式が成立することを示せ、繰り返し評価することで

[math]
\|\mathbf{w}^k\|^2 \leq k \eta^2 D^2
[/math]

が成立します。これより

[math]
\begin{eqnarray}
\cos \theta^k &=& \dfrac{\mathbf{u}^T\mathbf{w}^k}{\|\mathbf{w}^k\|}\\
&\geq & \dfrac{k\eta \gamma}{\sqrt{k}\eta D}\\
&=& \sqrt{k}\dfrac{\gamma}{D}
\end{eqnarray}
[/math]

が成立し、[math]\cos \theta^k \leq 1[/math]より

[math]
k \leq \dfrac{D^2}{\gamma^2}
[/math]

となり右辺は定数なので有限回の反復で終了することが分かります。

単純パーセプトロンの限界

パーセプトロンの収束定理から線形分離可能な問題が解けることが分かった一方

線形分離不可能な問題は収束しない

ことが指摘され、かなり簡単な問題しか解けないことがはっきりしました。

実際、上の例で負例集合の中に正例を1つ混ぜると収束しなくなってしまいます。

いったん下火になったニューラルネットワークですが、単純パーセプトロンに隠れ層を追加した「3層ニューラルネットワーク」は強力な表現力を持っていることが示され再び脚光を浴びることになります。

シリーズ記事

• ニューラルネットワークの基本要素：ユニット
• ニューラルネットワークの構造とその歴史
• 単純パーセプトロンの収束定理と限界（本記事）