モンティ・ホール問題
アメリカのゲームショー[1]「モンティ・ホール」はこの番組の司会者です。の中で行われたゲームに由来する問題で大きな論争になったことで有名な問題です。
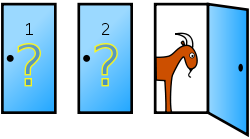
この問題が出た当初は多くの人が
「開けられていない2つのドアのどちらかが正解で、正解を選ぶ確率はそれぞれ[math]\frac{1}{2}[/math]なので選び直しても当たる確率は変わらない」
と回答しましたが、ベイズの定理を使うと「ドアを変えた方が良い」という結果が得られます。
まず、論争の原因の1つがゲームルールの解釈が複数あったためで混乱を避けるため改めてルールを明記すると
- ドアA, B, Cには(景品、ヤギ、ヤギ)がランダムに入っている
- 回答者はドアを1つ選ぶ
- 司会者は残りのドアのうち1つを必ず開ける
- 司会者は必ずヤギの入っているドアを開ける
- 司会者は残りのドア2つともヤギの場合、ランダムに開ける
- 司会者はドアを選び直して良いと必ず言う
になります。回答者が最初に選んだドアをA、司会者が開いたドアをBとして[math]P(A), P(C)[/math]をドアA, Cが当たりである事前確率、ドアBが開いたという前提での事後確率[math]P(A|B_{OPEN}),P(C|B_{OPEN})[/math]がどうなるか?を計算する問題になります。ここで、ベイズの定理を使うと
[math]P(A|B_{OPEN})=\dfrac{P(B_{OPEN}|A)P(A)}{P(B_{OPEN}|A)P(A)+P(B_{OPEN}|C)P(C)}[/math]
で[math]P(B_{OPEN}|A)[/math]は「ドアAが当たりの時にドアBを開ける確率」なのでルール5より[math]\frac{1}{2}[/math]になり、[math]P(B_{OPEN}|C)[/math]はルール3, 4よりドアBを開けるしかないので確率は1になります。これより
[math]P(A|B_{OPEN})=\dfrac{\frac{1}{2}\cdot\frac{1}{3}}{\frac{1}{2}\cdot\frac{1}{3}+1\cdot\frac{1}{3}}=\dfrac{1}{3}[/math]
および
[math]P(C|B_{OPEN})=\dfrac{1\cdot\frac{1}{3}}{\frac{1}{2}\cdot\frac{1}{3}+1\cdot\frac{1}{3}}=\dfrac{2}{3}[/math]
となり「ドアを変更することで当たる確率が2倍になる」ことがわかります。
ポイントは司会者が「必ずヤギが入っているドアを開ける」というルールのため開けられていないドアは対等ではなく、司会者に開けなかったドアに当たりである確率が集中するところです。このポイントをイメージでわかりやすく説明しているのがWikipediaの説明で
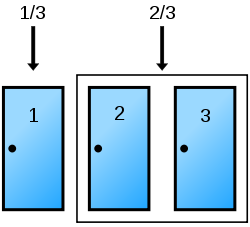
最初、回答者が選んだドアが当たりの確率は[math]\frac{1}{3}[/math]で残りの2つのドアが[math]\frac{2}{3}[/math]です。ここで司会者が「ヤギが入っているドア」を開けると
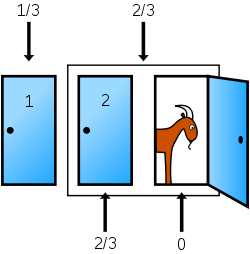
開けられなかったドアに当たりの確率[math]\frac{2}{3}[/math]が集中することなり「ドアを変更した方が当たる確率が2倍になる」ということも直感的に理解できると思います。
参考文献
脚注
| ↑1 | 「モンティ・ホール」はこの番組の司会者です。 |
|---|