確率変数の相関係数

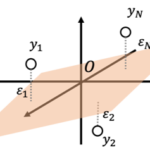
2つの確率変数が直線関係があるかを示す指標として相関係数（correlation coefficient）があります。

単に「相関係数」という場合には2つのデータ系列[math](x_i,\ y_i),\ i=1,\dots,n[/math]間の直線関係を表す「ピアソンの積率相関係数」が有名ですがここでは確率変数[math]X, Y[/math]の相関係数について定義と以下の性質

• スケール不変性
• とりうる値の範囲
• [math]X, Y[/math]の線形性との関係
• [math]X, Y[/math]の独立性との関係

を紹介します。

定義

確率変数[math]X, Y[/math]はそれぞれ平均[math]\mu_X, \mu_Y[/math]、分散[math]\sigma_X^2\ne 0, \sigma_Y^2\ne 0[/math]が存在するとします。

このとき確率変数[math]X, Y[/math]の相関係数[math]\rho_{X,Y}[/math]を

[math]
\rho_{X,Y}=\dfrac{{\rm Cov}(X, Y)}{\sigma_X\sigma_Y}
[/math]

で定義します。ここで[math]{\rm Cov}(X, Y)[/math]は確率変数[math]X, Y[/math]の共分散で[math]{\rm Cov}(X, Y)=E\left[(X-\mu_X)(Y-\mu_Y)\right][/math]です。

ここから相関係数の性質をみていきます。

スケール不変性

まず基本的な性質としてスケール不変性、つまり確率変数の線形変換に対して相関係数は変化しないという性質があります。

証明は共分散、分散の性質から

• [math]{\rm Cov}(V, W)=ac\cdot{\rm Cov}(X, Y)[/math]
• [math]\sigma_V=a\cdot\sigma_X,\ \sigma_W=c\cdot\sigma_Y[/math]

なので相関係数の定義から[math]\rho_{V,W}=\rho_{X,Y}[/math]になります。

とりうる値の範囲

相関係数は[math][-1,\ 1][/math]の範囲をとることが知られています。

まず補題として以下を示します。

証明の概略を示すと[math]f(t)=E[(X-tY)^2][/math]とおくと定義より任意の[math]t[/math]で[math]f(t)\geq 0[/math]です。

ここで、[math]f(t)[/math]を展開し[math]t[/math]の二次式とみて最小値を求めます。計算すると[math]t^*=\frac{E[XY]}{E[Y^2]}[/math]のときに最小値[math]f(t^*)=E[X^2]-\frac{E[XY]^2}{E[Y^2]}\geq 0[/math]となることから[math]E[XY]^2 \leq E[X^2]E[Y^2][/math]を得ます。等号が成立するのは確率[math]1[/math]で[math]X=tY[/math]が成立するときに限ります。

では、補題を使って相関係数の範囲を評価しましょう。スケール不変性から確率変数[math]X, Y[/math]の平均を[math]0[/math]としても一般性を失いません^[1]平均を引いた確率変数を改めて[math]X, Y[/math]とみなせばよいです。。

このとき[math]\sigma_X^2=E[X^2]-E[X]^2=E[X^2][/math]となり、同様に[math]\sigma_Y^2=E[Y^2][/math]なので

[math]
\begin{eqnarray}
\rho_{X, Y}^2 &=& \dfrac{{\rm Cov}(X, Y)^2}{\sigma_X^2\sigma_Y^2} \\
&=& \dfrac{E[XY]^2}{E[X^2]E[Y^2]} \\
&\leq & 1
\end{eqnarray}
[/math]

が成立し[math]-1 \leq \rho_{X, Y} \leq 1[/math]が成立します。

[math]X, Y[/math]の線形性との関係

ここでも確率変数[math]X, Y[/math]の平均を[math]0[/math]として議論を進めます。

まず[math]X, Y[/math]に線形関係がある場合、相関係数は[math]1[/math]または[math]-1[/math]になります。

[math]{\rm Cov}(X, Y)=aE[X^2][/math]および[math]\sigma_Y=|a|\sigma_X[/math]より[math]\rho_{X, Y}=\dfrac{a}{|a|}[/math]なので[math]a[/math]が正なら[math]1[/math]、負なら[math]-1[/math]になることがわかります。

逆は上の「相関係数の範囲」で等号が成立するケースで以下になります。

なお、相関係数はあくまでも2つの確率変数の間に直線関係があるかを見るための指標です。次の例からわかるように相関係数が[math]0[/math]に近くても「直線関係はない」としか言えず何らかの非線形な関係がありうることには注意しましょう。

[math]E[X]=0, E[Y]=E[X^2]-1=0[/math]より共分散を求めると

[math]
\begin{eqnarray}
{\rm Cov}(X, Y) &=& E[X(X^2-1)] \\
&=& E[X^3]-E[X] \\
&=& 0
\end{eqnarray}
[/math]

より相関係数[math]\rho_{X, Y}=0[/math]である。

この例では相関係数は0ですが[math]X, Y[/math]の間には[math]Y=X^2-1[/math]と非線形な関係があります。

[math]X, Y[/math]の独立性との関係

同様に確率変数[math]X, Y[/math]の平均を[math]0[/math]とします。[math]X, Y[/math]が独立の時、相関係数は[math]0[/math]になります。

独立性から期待値の積を分解でき[math]E[XY]=E[X]E[Y]=0[/math]より[math]\rho_{X, Y}=0[/math]を得ます。

逆は一般には成立せず[math]\rho_{X,Y}=0[/math]であっても[math]X, Y[/math]が独立とは限りません。しかし、[math]X, Y[/math]が2次元正規分布に従う場合は[math]\rho_{X,Y}=0[/math]ならば独立になります。

証明の概略としては2次元正規分布の同時確率密度関数において[math]\rho_{X,Y}=0[/math]を考えると1次元正規分布の確率密度関数の積で表せることから[math]X, Y[/math]は独立であることを示せます。