続いて学習/評価データの基礎集計をしていきます。基礎集計では
- 異常値(定義上、ありえない値)がないか
- 分布の確認
- 外れ値がないか
- 頻度の少ないデータがないか
- 学習、評価データで分布に偏りがないか
を確認し、適切な前処理を検討することがポイントです。なお、notebookはGithubにアップしています。
生存フラグ(Survived)
0 or 1の数値が入っており学習データ891人中の生存者は342人(38%)です。
乗客の4割しか生存できなかったと考えると少ないですが、2値分類としてみると正例と負例が4:6とバランスが取れています。正例/負例に大きな偏りがある[1]不均衡データ(imbalanced data)と呼ばれます。場合、重み付けやサンプリングが必要になりますが、今回は特に必要なさそうです。
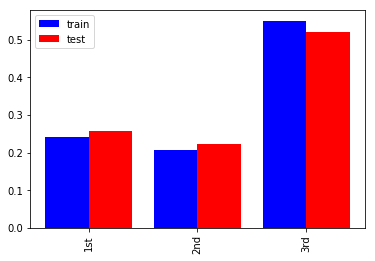
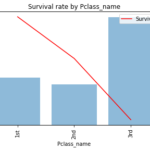
チケットのクラス(PClass)
1st、2nd、3rdがおおよそ1:1:2の比率になっています。評価データは学習データとほぼ同じ分布ですが1st, 2ndが1-2%多く、3rdが3%少ないです。
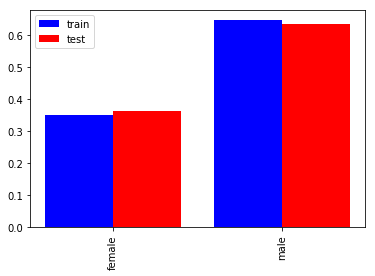
性別(Sex)
男女比は2:1で男性の方が多いです。学習、評価データともに同様の構成比率ですね。
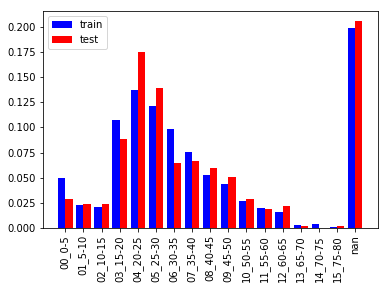
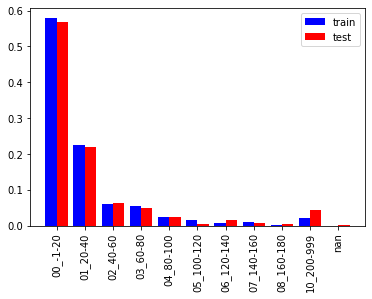
年齢 (Age)
上図は5才刻みのヒストグラムです。15〜40才の乗客が多く全体の半数を占めています。また、65才以上の乗客は少ないためまとめた方が良いでしょう。
学習/評価データで分布に少し違いがあり評価データは学習データと比べ
- 5才未満、15-20才, 30-35才が2%程度少ない
- 20-30才が2-3%程度多い
となっています。年齢カテゴリを作る際はこの分布の違いを考慮した方が良いかもしれません。
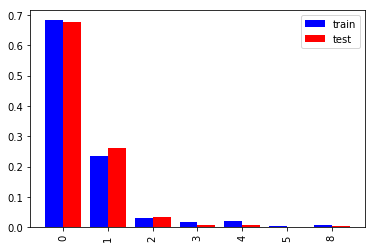
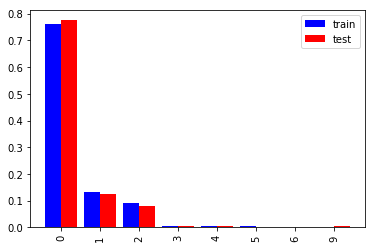
一緒に乗船した兄弟、配偶者の数(SibSp)
約9割が0か1になっているので2以上をまとめるのも良いでしょう。評価データは学習データとほぼ同じ分布ですが1が3%程度多く、3以上がその分少ないです。
一緒に乗船した親子の数(Parch)
最大値が学習データは6ですが、評価データでは9と少し外れています。95%程度が2以下であることも合わせ、3以上をまとめた方が良いでしょう。
運賃(Fare)
20刻みで描いたヒストグラムです。裾の長い分布なので回帰系のアルゴリズムを使う場合は外れ値を処理した方が良いでしょう。
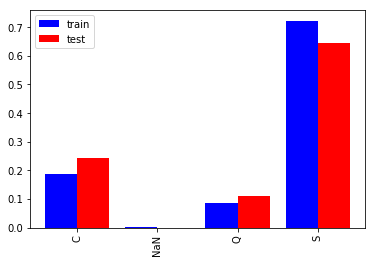
乗船港(Embarked)
Sが最も多く7割近くを占めます。学習と評価で構成比率に少し差があり評価データは学習データと比べSが8%ほど少なく、C、Qが4%程度多いです。
名前(Name)、チケット(Ticket)、客室番号(Cabin)
これらのデータは大多数が異なる値になっておりそのままでは使えません。もちろん、加工して有用な情報を取り出せる可能性はあるので特徴量として作った際に改めて基礎集計をすることにします。
基礎集計のまとめ
基礎集計の結果を踏まえ、今後の分析で留意すべき点をまとめておきましょう。
- 目的変数である生存有無(Survived)の比率は4:6と大きな偏りはない
- 年齢(Age)は65才以上は少ないためまとめた方が良い
- 年齢(Age)は学習/評価データで分布に少し違いがある
- SibSpは2以上は1割未満なのでまとめた方が良さそう
- Parchは3以上は5%未満なのでまとめた方が良さそう
- 運賃(Fare)は裾の長い分布なので回帰系を使う場合は外れ値を処理する
- 乗船港(Embarked)は学習/評価データで分布に少し違いがある
- Name, Ticket, Cabinは加工が必要
続いて目的変数である生存フラグと各特徴量のクロス集計をしましょう。
脚注
| ↑1 | 不均衡データ(imbalanced data)と呼ばれます。 |
|---|