重回帰モデルと決定係数の関係

重回帰モデルでも単回帰モデルと同様に決定係数[math]D[/math]と相関係数[math]\rho[/math]の関係

[math]

D = \rho^2
[/math]

を導くことができます。

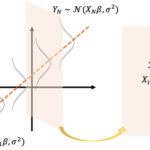
重回帰モデル

重回帰は[math]P[/math]個の説明変数[math]x_{1},\ x_{2},\dots,\ x_{P}[/math]と目的変数[math]y[/math]の間の関係

[math]

y = \beta_0 + \beta_1 x_1 + \cdots + \beta_P x_P,\ \beta_0, \dots, \beta_P \in \mathbb{R}
[/math]

を[math]N[/math]個の学習データ、つまり入出力データの組

• 入力データ: [math](x_{i,1},\ x_{i,2},\dots,\ x_{i,P}) \in \mathbb{R}^P[/math]
• 出力データ: [math]y_i\in \mathbb{R}[/math]

から求める手法です[math](i=1,2,\dots,N)[/math]。

表記を簡単にするために行列、ベクトルを定義しておきます。

• 説明変数: [math]\boldsymbol{x}=(1,x_1,\dots,x_P)^T\in \mathbb{R}^{P+1}[/math]
• 回帰係数: [math]\boldsymbol{\beta}=(\beta_0,\beta_1,\dots,\beta_P)^T\in \mathbb{R}^{P+1}[/math]
• 学習データ
  • 出力データ: [math]\boldsymbol{y}=(y_1,\dots,y_N)^T\in\mathbb{R}^N[/math]
  • 入力データ:
    [math]
    \begin{eqnarray}
    
\boldsymbol{e} &=& (1,\ 1,\dots,\ 1)^T\in\mathbb{R}^N \\
    \boldsymbol{x}_i &=& (x_{1,i},\ x_{2,i},\dots,\ x_{N,i})^T\in\mathbb{R}^N \\
    \boldsymbol{X} &=& \left(
\boldsymbol{e}\ 
\boldsymbol{x}_1 \cdots \boldsymbol{x}_P \right)\in \mathbb{R}^{N \times (P+1)}
    \end{eqnarray}
    [/math]

決定係数

決定係数とは機械学習モデルが学習データにどれだけ当てはまっているかを評価する指標です。モデルの予測値を[math]\boldsymbol{\hat{y}}=(\hat{y}_1,\dots,\hat{y}_N)[/math]として決定係数[math]D[/math]は

[math]

\displaystyle D := 1 – \dfrac{\|\boldsymbol{y}-\boldsymbol{\hat{y}}\|^2}{\|\boldsymbol{y}-\bar{y}\boldsymbol{e}\|^2}
[/math]

で与えられます。ここで[math]\bar{y}=\frac{1}{N}\sum_{i}y_i[/math]です。決定係数の意味、性質については「単回帰モデルと決定係数の関係」を参照ください。

重回帰モデルでの決定係数と相関係数の関係

ここからはモデルが重回帰の場合を考えます。つまり

[math]


y = \hat{\beta}_0 + \hat{\beta}_1 x_1 + \cdots + \hat{\beta}_P x_P
[/math]

で予測するモデルを考えます。

この時、出力データ[math]y_i[/math]と入力データの予測値[math]\hat{y}_i[/math]の相関係数[math]\rho[/math]

[math]
\rho = \dfrac{(\boldsymbol{y} – \bar{y}\boldsymbol{e})^T(\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e})}{\|\boldsymbol{y} – \bar{y}\boldsymbol{e}\|\|\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}\|}
[/math]

と決定係数[math]D[/math]には次の関係が成立します。

全変動の平方和の分解

重回帰モデルの出力データ[math]\boldsymbol{y}[/math]とその予測値[math]\boldsymbol{\hat{y}}[/math]に対して「幾何学でみる重回帰の性質」の「全変動の平方和の分解」で見たように全変動の平方和を

[math]

\|\boldsymbol{y} – \bar{y}\boldsymbol{e}\|^2 = \|\boldsymbol{y} – \boldsymbol{\hat{y}}\|^2 + \|\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}\|^2
[/math]

と分解できます。これより決定係数は

[math]
\begin{eqnarray}


\displaystyle D &=& 1 – \dfrac{\|\boldsymbol{y}-\boldsymbol{\hat{y}}\|^2}{\|\boldsymbol{y}-\bar{y}\boldsymbol{e}\|^2} \\
&=& \dfrac{\|\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}\|^2}{\|\boldsymbol{y}-\bar{y}\boldsymbol{e}\|^2}
\end{eqnarray}
[/math]

とかけます。

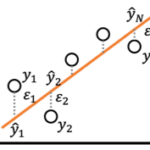
つぎに相関係数[math]\rho=\frac{(\boldsymbol{y} – \bar{y}\boldsymbol{e})^T(\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e})}{\|\boldsymbol{y} – \bar{y}\boldsymbol{e}\|\|\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}\|}[/math]を整理していきます。分子の内積は[math]\boldsymbol{y} – \bar{y}\boldsymbol{e}[/math]を

[math]
\begin{eqnarray}

\boldsymbol{y} – \bar{y}\boldsymbol{e} &=& (
\boldsymbol{y} – \boldsymbol{\hat{y}}) + (\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}) \\
&=& \boldsymbol{\varepsilon} + (\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e})
\end{eqnarray}
[/math]

と直交成分に分解して内積を考えると

[math]
\begin{eqnarray}

(\boldsymbol{y} – \bar{y}\boldsymbol{e})^T(\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}) &=& \boldsymbol{\varepsilon}^T(\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}) + \|\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}\|^2 \\
&=& \|\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}\|^2
\end{eqnarray}
[/math]

となるので

[math]

\rho=\dfrac{\|\boldsymbol{\hat{y}} – \bar{\hat{y}}\boldsymbol{e}\|}{\|\boldsymbol{y}-\bar{y}\boldsymbol{e}\|}
[/math]

を得ます。これより

[math]

D = \rho^2
[/math]

が成立します。残差[math]\boldsymbol{\varepsilon}[/math]の直交性をうまくつかうことで単回帰の時よりシンプルに示すことができます。

この結果から単回帰と同様に決定係数は[math]D=\rho^2 \geq 0[/math]が保証され「平均値で予測するモデル」と比べ（決定係数の意味で）当てはまりの良いモデルと言えます。

シリーズ記事

「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「重回帰」の性質を紹介しています。

誤差項について「無相関で分散一定」「独立同一な正規分布」を仮定するとで様々な性質を導くことができますが、ここでは誤差項について特に仮定せずに導ける性質として

• 考え方と基本的な性質: 回帰係数の導出、回帰超平面の性質、計算量との関係
• 幾何学的な解釈: 重回帰の性質を幾何的に導出
• 決定係数（本記事）: 決定係数と相関係数の関係
• 多重共線性

を解説しています。

また行列やベクトル演算が多く何をしているか理解しづらいと感じた方は説明変数が1つの場合である「単回帰」も参照ください。