Python（NumPy）による多次元正規乱数の生成

数値実験やシミュレーションを行う際に正規分布[math]\mathcal{N}(\mu, \sigma^2)[/math]や多次元正規分布[math]\mathcal{N}(\mathbf{\mu},\Sigma)[/math]に従う乱数が必要になることが良くあります。

Pythonの標準ライブラリであるrandomモジュールにも

random.gauss(mu, sigma)

という平均mu、標準偏差sigmaの正規乱数を返してくれる関数がありますが、

多次元正規分布を生成できない
多数の正規乱数をまとめて生成できない

と、本格的に使うには少し機能が不足しています。そこでNumPyで提供されているnumpy.randomモジュールを使った正規乱数生成を紹介します。なお、PythonスクリプトをGitHub上にアップしているのでそちらもご参照ください。

1次元正規乱数の生成

正規分布[math]\mathcal{N}(\mu, \sigma^2)[/math]に従う正規乱数を生成する関数として

numpy.random.normal(loc, scale, size)

が用意されています。引数には

loc: 生成したい正規分布の平均を指定(default=0)
scale: 生成したい正規分布の標準偏差を指定(default=1)
size: 生成する乱数の数を指定(default=None)

を指定します。

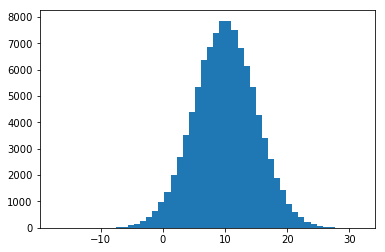
例えば平均[math]10[/math], 標準偏差[math]5[/math]に従う正規乱数を生成し、ヒストグラムを生成してみると

from numpy.random import *
from matplotlib import pyplot as plt

# 平均10, 標準偏差5の正規乱数を10万個生成
values = normal(10, 5, 100000)

# ヒストグラム
plt.hist(values, bins=50)
plt.show()

を実行すると以下のような結果が得られます。

多次元正規乱数の生成

多次元正規分布[math]\mathcal{N}(\mathbf{\mu},\Sigma)[/math]に従う正規乱数を生成する関数として

numpy.random.multivariate_normal(mean, cov, size, check_valid, tol)

が用意されています。引数には

loc: 生成したい正規分布の平均値ベクトルを指定
scale: 生成したい正規分布の分散共分散行列を指定
size: 生成する乱数の数を指定(default=1)
check_valid: 分散共分散行列の半正定値チェック有無(warn/raise/ignoreを指定。オプション)
tol: 半正定値チェックの許容誤差(オプション)

を指定します。

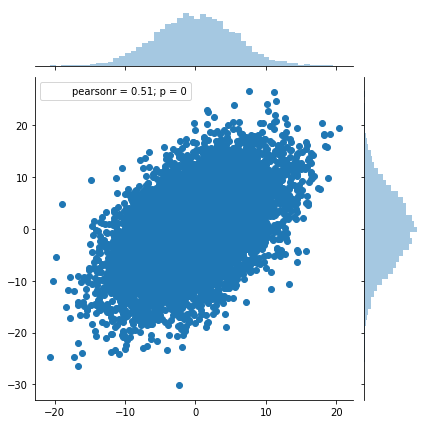
平均[math]\mathbf{\mu}=\begin{pmatrix}0 \\ 0 \end{pmatrix}[/math], 分散共分散行列[math]\Sigma = \begin{pmatrix}30 & 20 \\ 20 & 50 \end{pmatrix}[/math]とした時の正規乱数の生成は

from numpy.random import *
from matplotlib import pyplot as plt
import seaborn as sns

mu = [0, 0]
sigma = [[30, 20], [20, 50]]

# 2次元正規乱数を1万個生成
values = multivariate_normal(mu, sigma, 10000)

# 散布図
sns.jointplot(values[:,0], values[:,1])
plt.show()

を実行すると以下のような結果が得られます。