【統計検定1級過去問】2017年（理工学）大問1

ある電子部品の寿命[math]X[/math]はガンマ分布[math]Gamma(\alpha, \beta)[/math]に従うとする。ここで[math]Gamma(\alpha, \beta)[/math]の確率密度関数は

[math]
f(x)=\begin{cases}\dfrac{1}{\beta^\alpha \Gamma(\alpha)}x^{\alpha-1}e^{-x/\beta} &(x > 0) \\ 0 &(x \leq 0)\end{cases}
[/math]

である。[math]n[/math]個の電子部品の寿命の試験結果[math]X_1,\dots,X_n[/math]の実現値を[math]x_1,\dots,x_n[/math]とし[math]x_1=\cdots=x_n[/math]ではないとする。この時、以下の問に答えよ。

1. [math]E[X]=\alpha\beta[/math]および[math]V[X]=\alpha\beta^2[/math]であることを示せ。
2. 対数尤度関数[math]l(\alpha, \beta;\ \mathbf{x})[/math]を求めよ。
3. 尤度方程式から[math]\psi(\alpha)-\log\alpha=\log\dfrac{\tilde{x}_n}{\bar{x}_n}[/math]および[math]\beta=\dfrac{\bar{x}_n}{\alpha}[/math]を導けることを示せ。ここで[math]\bar{x}_n=\frac{1}{n}\sum_{i=1}^n x_i[/math], [math]\tilde{x}_n=\left(\prod_{i=1}^n x_i\right)^{1/n}[/math]であり[math]\psi(\alpha)[/math]は対数ガンマ関数の1次導関数（ディガンマ関数）である。
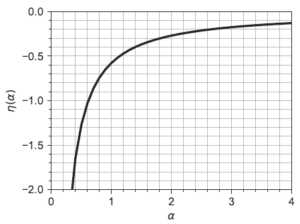
4. [math]\bar{x}_n=1000[/math], [math]\log\tilde{x}_n=6.36[/math]の時、[math]\alpha, \beta[/math]の最尤推定量を求めよ。なお、[math]\eta(\alpha)=\psi(\alpha)-\log\alpha[/math]のグラフは以下になる。



5. 一般の場合に[math]\alpha, \beta[/math]の最尤推定値が一意的に存在することを示せ。ここで[math]\eta(\alpha)=\psi(\alpha)-\log\alpha[/math]は[math]\alpha\in (0,\infty)[/math]で単調増加関数になることは用いてよい。